2006届南昌市高三第一次模拟考试题
2006.3.9
一.选择题:(5×12分)
1.
命题“若![]() ,则
,则![]() ”的逆否命题是
( D
)
”的逆否命题是
( D
)
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若a ≤b,则![]() D.若
D.若![]() ,则a ≤b
,则a ≤b
2.将函数![]() 的图象按向量
的图象按向量![]() 平移后所得图象的解析式是( A )
平移后所得图象的解析式是( A )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.已知![]() 是平面,
是平面,![]() 是直线.下列命题中不正确的是 ( B )
是直线.下列命题中不正确的是 ( B )
A.若![]() ,
,![]() ,则
,则![]() B.若
B.若![]() ,
,![]() ,则
,则![]()
C.若![]() ,
,![]() ,则
,则![]() D.若
D.若![]() ,
,![]() ,则
,则![]()
4.在锐角![]() 中,若
中,若![]() ,则
,则![]() 的取值范围为( A )
的取值范围为( A )
A.![]() B.(1,
B.(1,![]() )
)
C.![]() D.(―1,1)
D.(―1,1)
5.(理)定义运算![]() ,则符合条件
,则符合条件![]() 的复数z为 ( A )
的复数z为 ( A )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
(文) 已知二项式![]() 展开式的第4项与第5项之和为零,那么
展开式的第4项与第5项之和为零,那么![]() 等于 ( C )
等于 ( C )
A.1
B.![]() C.2
D.46
C.2
D.46
6.一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为( D )
A.3π B.4π C.![]() D.6π
D.6π
7.设抛物线![]() 的准线与
的准线与![]() 轴交于点Q,若过点Q的直线
轴交于点Q,若过点Q的直线![]() 与抛物线有公共点,则直线
与抛物线有公共点,则直线![]() 的斜率的取值范围是
(B )
的斜率的取值范围是
(B )
A.![]() B.[-1,1] C.[-2,2] D.[-4,4]
B.[-1,1] C.[-2,2] D.[-4,4]
8.互不相等的三个正数![]() 成等比数列,且点
成等比数列,且点
P1(![]()
![]() 共线
共线
![]() 则
则![]() ,
,![]() ( C )
( C )
A.等差数列,但不等比数列; B.等比数列而非等差数列
C.等比数列,也可能成等差数列 D.既不是等比数列,又不是等差数列
9.(理)设实数![]() 满足
满足![]() ,
,![]() ,
,![]() ,则
,则![]() 与
与![]() 的大小关系为 (
C )
的大小关系为 (
C )
A.![]()
![]()
![]() B.
B.![]()
![]()
![]()
C.![]()
![]()
![]() D.不能确定,它们的大小与
D.不能确定,它们的大小与![]() 有关
有关
(文) 不等式![]() 的解集是
(B )
的解集是
(B )
A. ![]() B.
B. ![]()
C. ![]() D.
D.
![]()
10.若函数![]() 即是奇函数,又是增函数,那么
即是奇函数,又是增函数,那么![]() 的图象是 ( D )
的图象是 ( D )
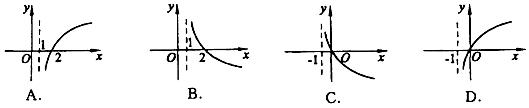
11.从6人中选出4人加数、理、化、英语比赛,每人只能参加其中一项,其中甲、乙两人
都不能参加英语比赛,则不同的参赛方案的种数共有 ( C )
A.96 B.180 C.240 D.288
12.已知![]() 的反函数为
的反函数为![]() ,则( B )
,则( B )
A ![]() B
B ![]()
C ![]() D
D ![]()
二.填空题:(4×4分)
13.(理)设函数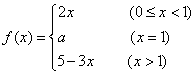 在区间
在区间![]() 上连续,则实数a的值为
__2___.
上连续,则实数a的值为
__2___.
(文)在等差数列![]() __13___.
__13___.
11.函数![]() 的定义域为_
的定义域为_![]() ;值域为
;值域为 ![]() 。
。
15.已知变量x、y满足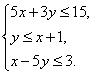 ,若使z=x+ky最小的最优解有无穷多个,则k的值是__-1____。
,若使z=x+ky最小的最优解有无穷多个,则k的值是__-1____。
16.将侧棱相互垂直的三棱锥称为“直角三棱锥”,三棱锥的侧面和底面分别叫为直角三棱锥的“直角面和斜面”;过三棱锥顶点及斜面任两边中点的截面均称为斜面的“中面”.请仿照直角三角形以下性质:(1)斜边的中线长等于斜边边长的一半;(2)两条直角边边长的平方和等于斜边边长的平方;(3)斜边与两条直角边所成角的余弦平方和等于1.
写出直角三棱锥相应性质(至少一条): .
16.(1)斜面的中面面积等于斜面面积的四分之一;(2)三个直角面面积的平方和等于斜面面积的平方;(3)斜面与三个直角面所成二面角的余弦平方和等于1.
三.解答题:(共74分)
17.(本小题满分12分)
已知:![]() (
(![]() 为常数)
为常数)
(I)若![]() ,求
,求![]() 的最小正周期;
的最小正周期;
(II)若![]() 在
在![]() 上最大值与最小值之和为3,求a的值。
上最大值与最小值之和为3,求a的值。
解:![]() ……3分
……3分
![]() ……5分
……5分
(I)![]() 的最小正周期
的最小正周期![]() ……6分
……6分
(II)由![]() 知
知![]() ……8分
……8分
![]()
![]() ……10分
……10分
![]()
![]() ,解得
,解得![]() ……12分
……12分
18. (本小题满分12分)
某人抛掷一枚硬币,出现正反的概率都是![]() ,构造数列
,构造数列![]() ,使得
,使得 ,记
,记![]() 。
。
(1)
求![]() 的概率;
的概率;
(2)
求:前两次均出现正面,且![]() 的概率。
的概率。
(3)
(理科做文科不做)记![]() ,求
,求![]() 的数学期望。
的数学期望。
解:(1)![]() ,需4次中有3次正面1次反面,设其概率为
,需4次中有3次正面1次反面,设其概率为![]()
则![]()
(2)6次中前两次均出现正面,要使![]() ,则后4次中有2次正面、2次反面或3次正面、1次反面。设其概率为
,则后4次中有2次正面、2次反面或3次正面、1次反面。设其概率为![]() 。
。
![]()
(3)6次中前两次均出现正面,记后4次中出现正面![]() 次,则
次,则![]()
![]() ~B(4,
~B(4,![]() ),
),
![]() ,
,
又![]() ,
,![]() 。
。
19. (本小题满分12分)
(本小题满分12分)
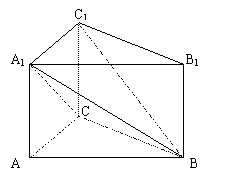
已知直三棱柱ABC—A1B1C1中,AB= 4,AC=AA1=2,∠CAB=60°。
(1) 求证:A1C⊥B1C1;
(2) 求点B1到平面A1BC的距离;
(3) 求二面角C1—A1B—C的大小。
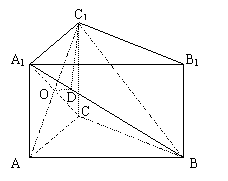 19.解法(一):(1)在△ABC中
19.解法(一):(1)在△ABC中
![]()
![]()
![]()
![]() ,即
,即![]() ,
,
由直三棱柱性质知:平面ACC1A1⊥平面ABC。
∴BC⊥平面ACC1A1
∴BC⊥A1C 又BC∥B1C1
∴B1C1⊥A1C ……………………………………………………………… 4分
(2)∵BC∥B1C1,![]() 平面ABC,
平面ABC,
∴B1C1∥平面A1CB
∴B1点到平面A1CB的距离等于点C1到平面A1CB的距离。……………………6分
设点B1点到平面A1CB的距离为![]() ,则
,则
![]()
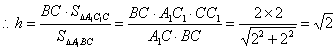 ………………………8分
………………………8分
(3)连结AC1,交A1C于O,过O作OD⊥A1B于D,连结C1D
由(1)BC⊥平面ACC1A1得:平面BCA1⊥平面ACC1A1
由正方形ACC1A1知AC1⊥A1C
∴C1A⊥平面A1BC
∴OD是C1D在平面A1BC上的射影
∴C1D⊥A1B(三垂线定理)
∴∠ODC1是二面角C1—A1B—C的平面角。……………………………………10分
在△A1BC中,A1B=![]() ,BC=
,BC=![]() ,A1C=
,A1C=![]() ,A1O=
,A1O=![]() 。
。
由![]() 得:
得:![]()
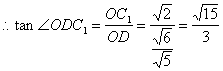
∴二面角C1—A1B—C的大小是![]() ……………………………………12分
……………………………………12分
解法(二)先证![]() ,然后以C为原点,分别以CA、CB、CC1为
,然后以C为原点,分别以CA、CB、CC1为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系(略)
轴建立空间直角坐标系(略)
20.(本小题满分12分)
(理)已知a>1,函数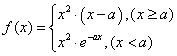 ,求函数f(x)在
,求函数f(x)在![]() 时的最小值。
时的最小值。
解:一.![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
![]() 时是增函数,
时是增函数,
![]() ;
;
二.1<a≤2时,![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,
,
![]() ;
;
三.![]() 时,
时,![]() ,
,
![]() ,
,
![]() 时是减函数
时是减函数
![]()
(文)已知![]() ,求函数
,求函数![]() 的单调区间。
的单调区间。
解:![]()
一.a=0时,![]() 递增区间是
递增区间是![]() ;
;
二.a>0时,![]() ,
,
递增区间是![]() ;
;
三.a<0时,![]() ,
,
(1)-2<a<0时,递增区间是![]() ;
;
(2)a=-2时,无递增区间;
(3)a<-2时,递增区间是![]() 。
。![]()
21.(本小题满分12分)
已知抛物线C的顶点在原点,以双曲线![]() 的左准线为准线,(1)求抛物线C的方程;(2)A是抛物线C上任一点,A关于x轴的对称点为B,过A作抛物线的弦AP、AQ,且AP⊥AQ,是否存在常数h,使得
的左准线为准线,(1)求抛物线C的方程;(2)A是抛物线C上任一点,A关于x轴的对称点为B,过A作抛物线的弦AP、AQ,且AP⊥AQ,是否存在常数h,使得![]() ?
?
解:(1)双曲线的左准线为x=-1,![]() 抛物线方程是
抛物线方程是![]() ;
;
(2)设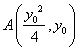 ,AP的直线方程为
,AP的直线方程为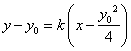 ,
,
将抛物线方程![]() 代入AP的直线方程,得
代入AP的直线方程,得![]() ,
,
 ,
,
同理:![]() ,
,
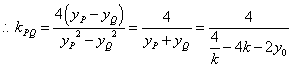 ,
,
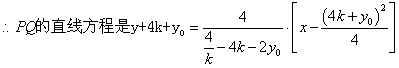 ,
,
令![]() ,
,
![]()
![]() 点的坐标是
点的坐标是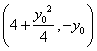 ,
,
∴存在h=4,使得![]() 且
且![]()
22.(本小题满分14分)
已知数列![]() 满足
满足![]() .(1)求数列
.(1)求数列![]() 的通项公式;(2)设a>0,数列
的通项公式;(2)设a>0,数列![]() 满足
满足![]() ,若
,若![]() 对
对![]() 成立,试求a的取值范围。
成立,试求a的取值范围。
解:(1)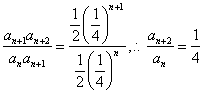 ,
,![]() 又
又![]() ,
,
![]() 是公比为
是公比为![]() 的等比数列,
的等比数列,![]()
(2)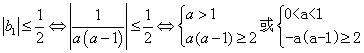
![]() ,
,
现证:![]() 时,
时,![]() 对
对![]() 成立。
成立。
①
n=1时,![]() 成立;
成立;
②
假设n=k(k≥1)时,![]() 成立,则
成立,则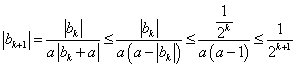 ,
,
即n=k+1时,![]() 也成立,
也成立,![]() 时,
时,![]()
![]() a的取值范围是
a的取值范围是![]() 。
。
22.(文)已知数列![]() 满足
满足![]() .(1)求数列
.(1)求数列![]() 的通项公式;(2)若数列
的通项公式;(2)若数列![]() 的前n项和
的前n项和![]() ,
,![]() ,求证:
,求证:![]() 。
。
解:(1)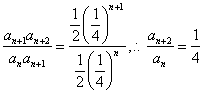 ,
,![]() 又
又![]() ,
,
![]() 是公比为
是公比为![]() 的等比数列,
的等比数列,![]()
(2)![]() ,
,
![]() ……①,
……①,![]() ②,①-②得:
②,①-②得:
![]() ,
,![]()
![]()