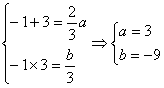2006届江苏省南通中学高三调研试卷
数 学 试 卷
命题人 赵栋
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至8页,共150分.考试时间120分钟.
第Ⅰ卷(选择题,共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.
3.考试结束,监考人将本试卷和答题卡一并收回.
参考公式:
如果事件A、B互斥,那么
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率
![]()
正棱锥、圆锥的侧面积公式S锥体侧=![]() 其中c表示底面周长, l表示斜高或母线长
其中c表示底面周长, l表示斜高或母线长
球的体积公式![]() 球=
球= ![]() 其中R表示球的半径
其中R表示球的半径
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题意要求的。
1.已知f(x)=3x,则f-1(9)的值为
A.-3 B.3 C.-2 D.2
2.不等式![]() 的解集是
的解集是
A.{x︱x>-2} B.{x︱x<-2}
C.{x︱-2<x<1或x>1} D.{x|x<-2或x>1}
3.若点P(3,4)、Q(a,b)关于直线![]() 对称,则
对称,则
A.a = 1,b =![]() B.a = 2,b
=
B.a = 2,b
= ![]() C.a = 4,b
= 3 D.a = 5,b
= 2
C.a = 4,b
= 3 D.a = 5,b
= 2
4.![]() 在点M处切线斜率为3,则点M的坐标为
在点M处切线斜率为3,则点M的坐标为
A.(0,-2) B.(1,0) C.(0,0) D.(1,1)
5.已知直线m、n,平面![]() ,则
,则![]() 的一个充分不必要条件为
的一个充分不必要条件为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.抛物线![]() 按向量e 平移后的焦点坐标为 (3,2),则平移后的抛物线顶点坐标为
按向量e 平移后的焦点坐标为 (3,2),则平移后的抛物线顶点坐标为
A.(4,2) B.(2,2) C.(-2,-2) D.(2,3)
 7.某电视台在因特网上就观众对其某一节目的喜爱程度进行调查,参加调查的人数为20000人,其中持各种态度的人数如右表所示.电视台为了了解观众的具体想法和意见,打算从中抽选出100人进行更为详细的调查,为此要进行分层抽样,那么在分层抽样时,每类人中各应抽选出的人数近似为
7.某电视台在因特网上就观众对其某一节目的喜爱程度进行调查,参加调查的人数为20000人,其中持各种态度的人数如右表所示.电视台为了了解观众的具体想法和意见,打算从中抽选出100人进行更为详细的调查,为此要进行分层抽样,那么在分层抽样时,每类人中各应抽选出的人数近似为
A.25,25,25,25 B.24,36,32,8
C.20,40,30,10 D.48,72,64,16
8.若函数f(x)同时具有以下两个性质:①f(x)是偶函数,②对任意实数x,都有f(![]() )= f(
)= f(![]() ),则f(x)的解析式可以是
( )
),则f(x)的解析式可以是
( )
A.f(x)=cosx B.f(x)=cos(2x![]() ) C.f(x)=sin(4x
) C.f(x)=sin(4x![]() ) D.f(x) =cos6x
) D.f(x) =cos6x
9.已知正方体ABCD-A1B1C1D1的棱长为1,P是AA1的中点,E是BB1上的点,则PE+EC的最小值是
A.2 B.![]() C.
C.![]() D.
D.![]()
10.若f (x)是偶函数,且当x∈[0,+∞)时,f (x)![]() ,则不等式
,则不等式![]() 的解集是
的解集是
A.{x ![]() } B.{x
} B.{x ![]() 或
或![]() } C.{x
} C.{x ![]() } D.{x
} D.{x ![]() }
}
11.若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为![]() ,值域为
,值域为![]() 的“同族函数”共有
的“同族函数”共有
A.9个 B.8个 C.5个 D.4个
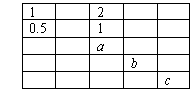 12.在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵行成等比数列,则a+b+c的值为
12.在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵行成等比数列,则a+b+c的值为
A.1 B.2
C.3 D.4
第Ⅱ卷(非选择题,共90分)
二、填写题:本大题共6小题,每小题4分,共24分。把答案填在答题卡相应位置。
13.二项式展开式![]() 中的常数项是
。
中的常数项是
。
14.已知![]() ,则
,则![]() =__________。
=__________。
15.在算式“4×□+1×□=30”的两个□中,分别填入两个自然数,使它们的倒数之和最小,则这两个数应分别为 。
16. 已知正四棱锥P-ABCD的高为4![]() ,侧棱与底面所成的角为60
,侧棱与底面所成的角为60![]() ,则该正四棱锥的侧面积
,则该正四棱锥的侧面积
是 .
17. 已知![]() ,
,![]() ,以
,以![]() 、
、![]() 为边作平行四边形OACB,则
为边作平行四边形OACB,则![]() 与
与![]() 的夹角为__________。
的夹角为__________。
18.已知![]() 、
、![]() 满足
满足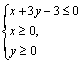 ,则
,则![]() 的取值范围是 .
的取值范围是 .
三、解答题:本大题共5小题,共66分。解答应写出文字说明、证明过程或演算步骤。
19.(本小题满分12分)
已知曲线C:x2+y2-2x-4y+m=0
(1)当m为何值时,曲线C表示圆;
(2)若曲线C与直线x+2y-4=0交于M、N两点,且OM⊥ON(O为坐标原点),求m的值。
20.(本小题满分12分)
同时抛掷15枚均匀的硬币一次
(1)试求至多有1枚正面向上的概率;
(2)试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?请说明理由.
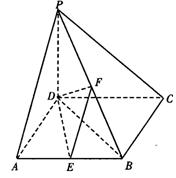
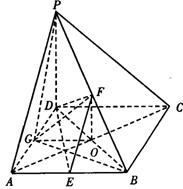
21(本小题满分14分,第一小问满分4分,第二、第三小问满分各5分)如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点.
|
(Ⅱ)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论;
(Ⅲ)求DB与平面DEF所成角的大小.
22. (本小题满分14分,第一小问满分6分,第二小问满分8分)已知函数![]()
(1)若函数![]() 在
在![]() 和
和![]() 时取得极值,试求
时取得极值,试求![]() 的值
的值
(2)在(1)的条件下,当![]() 时,
时,![]() <2|c|恒成立,求c的取值范围。
<2|c|恒成立,求c的取值范围。
23.(本小题满分14分,第一小问满分6分,第二问满分8分)
设{ak}为等差数列,公差为d,ak>0,k=1,2,……,2n+1.
(1)证明a>a2n-1·a2n+1;
(2)记bk=,试证lg b1+lg b2+……+lg bn>lg a2n+1-lg a1.
2005年7月高三质量调研卷
数学 答题卡
班级 考号 学号 姓名 得分
| 第Ⅰ卷 选择题 (共60分) | ||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||
| | ||||||||||||||||||||||||||||
| 第Ⅱ卷 非选择题 (共90分) | ||||||||||||||||||||||||||||
| 二.填空题: 13题 | ||||||||||||||||||||||||||||
|
14题 | ||||||||||||||||||||||||||||
| 15题 | ||||||||||||||||||||||||||||
| 16题 | ||||||||||||||||||||||||||||
| 17题 | ||||||||||||||||||||||||||||
| 18题 | ||||||||||||||||||||||||||||
| 三.解答题: 19题 解: |
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
| 20题 解:
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
| 21题 解:
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
| 22题 解:
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
| 23题 解:
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答
2005年7月高三质量调研卷
数学 答案
班级 考号 学号 姓名 得分
| 第Ⅰ卷 选择题 (共60分) | ||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||
| | ||||||||||||||||||||||||||||
| 第Ⅱ卷 非选择题 (共90分) | ||||||||||||||||||||||||||||
| 二.填空题: 13题 15 | ||||||||||||||||||||||||||||
|
14题 | ||||||||||||||||||||||||||||
| 15题 | ||||||||||||||||||||||||||||
| 16题
| ||||||||||||||||||||||||||||
| 17题 | ||||||||||||||||||||||||||||
| 18题 | ||||||||||||||||||||||||||||
| 三.解答题: 19题 解: 解:(1)由D2+E2-4F=4+16-4m=20-4m>0,得m<5。 (2)设M(x1,y1),N(x2,y2),由OM⊥ON得x1x2+ y1y2=0。 将直线方程x+2y-4=0与曲线C:x2+y2-2x-4y+m=0联立并消去y得 5x2-8x+4m-16=0,由韦达定理得x1+x2=
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
| 20题 解: 解:(1)记“抛掷1枚硬币1次出现正面向上”为事件A,P(A)= 则P1= P15(0)+ P15(1)= (2)记正面向上为奇数枚的概率为P2,则有 P2= P15(1)+ P15(3)+…+ P15(15)= = 又“出现正面向上为奇数枚”的事件与“出现正面向上为偶数枚” 的事件是对立事件,记“出现正面向上为偶数枚” 的事件的概率为P3
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
| 21题 解: (Ⅰ)(证法一)
(证法二)取BD的中点O,连结FO、OE.
(Ⅱ)答:G是AD的中点.…………5分 (方法一)取PC的中点H,连结DH.
(Ⅲ)设B到平面DEF的距离为d.
解法二:
D(0,0,0)、A(a,0,0)、B(a,a,0)、C(0,a,0)
(Ⅰ)
(Ⅱ)
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
| 22题 解: (1)∵函数 ∴ (2)
而 要使f(x)<2c恒成立,只要c+54<2c即可 当c≥0时c+54<2c ∴c>54 当c<0时c+54<-2c,∴c<-18 ∴c∈(-∞,-18)∪(54,+∞)
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
| 21题 解: (1)证明:a-a2n-1·a2n+1 =[a1+(2n-1)d]2-[a1+(2n-2)d][a1+2nd] =a12+(4n-2)a1d+(2n-1)2d2-[a12+(4n-2)a1d+(4n2-4n)d2] =d2>0 (d>0) ∴ a>a2n-1·a2n+1 …………………… (5分) (2)由(1)知> ∴ > > > …… > ∴()2·()2·()2 ·…·()2>()·()·()·…·= 即 b ·b ·b ·…·b > ……………………… (11分) ∴lg b1+lg b2+…+lg bn>lg a2n+1-lg a1 …………… (12分)
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答
请在各题目的答题区域内答题,超出黑色矩形框限定区域答案无效
| 22题 解:
|
请在各题目的答题区域内答题,超出黑色矩形框限定区域答





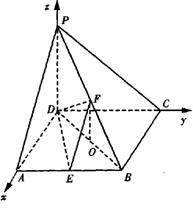
 (Ⅲ)设平面DEF的法向量为
(Ⅲ)设平面DEF的法向量为