昆明一中2005—2006学年度上学期期末高三一轮复习终结测试
数学试卷(理科) 2006.1
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第I卷1~2页,第II卷3~8页.全卷满分150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目等按要求涂写在答题卡上;答第Ⅱ卷前,考生务必将自己的姓名、班别、考号等填写在密封线左边的空格内,并在试卷右上角填上座位号.
2.第Ⅰ卷的答案必须答在答题卡上;第Ⅱ卷可用黑色或蓝色钢笔、圆珠笔按各题要求答在试卷上,但不能用铅笔或红笔.
3.考试结束时,将试题第Ⅱ卷和答题卡一并交回,第Ⅰ卷和草稿纸自己带走.
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1、若集合A={y│y=x![]() ,-1≤x≤1},B={y│y=2-
,-1≤x≤1},B={y│y=2-![]() ,0<x≤1},则A∩B等于
,0<x≤1},则A∩B等于
A. (-∞, -1] B. {1} C.Φ D. [-1,1]
2、设![]() ,
,![]() ,则满足条件
,则满足条件![]() ,
,![]() 的动点P的变化范围(图中阴影部分含边界)是A
的动点P的变化范围(图中阴影部分含边界)是A
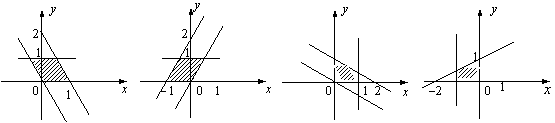 |
A . B. C . D.
3、设f(x)=2sin (![]() x+
x+![]() ),若对任意x∈R都有f (x
),若对任意x∈R都有f (x![]() )≤f (x) ≤f (x
)≤f (x) ≤f (x![]() )成立,则x
)成立,则x![]() -x
-x![]() 的最小是
的最小是
A.4
B.2
C.1
D.
![]()
4、![]() 的展开式中
的展开式中![]() 的系数等于
的系数等于
A 120
B 280
C ![]() D 35
D 35
5、已知数列![]() 满足
满足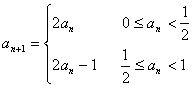 ,若
,若![]() ,则
,则![]()
A ![]() B
B
![]() C
C
![]() D
D
![]()
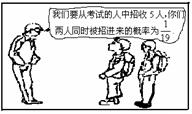 6、2006年香港大学首次在云南招生,因此两位同学去参加港大的英语口语考试,根据右图学校负责人与他们两人的对话,可推断出参加考试的人数为
6、2006年香港大学首次在云南招生,因此两位同学去参加港大的英语口语考试,根据右图学校负责人与他们两人的对话,可推断出参加考试的人数为
A. 19 B. 22 C.21 D.20
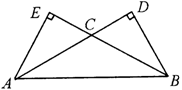 7、如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边
7、如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边
上的高分别为BD、AE,则以A、B为焦点,且过D、E
的椭圆与双曲线的离心率的倒数和为
A.![]() B.1 C.2
B.1 C.2![]() D.2
D.2
8、设函数f(x)=xsinx在x=x0处取得极值,则(1+![]() )(1+cos2x0)的值为
)(1+cos2x0)的值为
A.0 B.1 C.2 D.3
9、已知f(x)是定义在R上的奇函数,且是周期为2的周期函数,当x![]() [0,1]时,f(x)=2x-1,则f(log
[0,1]时,f(x)=2x-1,则f(log![]() 6)的值为
6)的值为
A.-![]() B.-
B.-![]() C.-5 D.-6
C.-5 D.-6
10、长方体的一个顶点上三条棱长分别是3,4,5,且它的八个顶点都在同一个球面上,则这个球的表面积是
A ![]() B
B
![]() C
C ![]() D
D ![]()
11、点P(-3,1)在椭圆![]() 的左准线上.过点P且方向为a=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为
的左准线上.过点P且方向为a=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为
A ![]() B
B
![]() C
C
![]() D
D
![]()
12、已知直线![]() (
(![]() 不全为
不全为![]() )与圆
)与圆![]() 有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有
有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有
A.66条 B.72条 C.74条 D.78条
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分。把答案填在答题卡相应位置。)
13、已知![]() 的夹角为45°,要使
的夹角为45°,要使![]() 垂直,则
垂直,则 ![]() .
.
14、平面内有n个圆两两相交,任何三个圆不过同一点,写出交点个数随着n的变化而变化的函数关系式f(n):_________________________________.
15、在R上定义运算![]() :x
:x![]() y=x(1-y),若不等式(x-a)
y=x(1-y),若不等式(x-a) ![]() (x+a)<1对任意实数x恒成立,则实数a的取值范围是
(x+a)<1对任意实数x恒成立,则实数a的取值范围是
16、给出下列四个命题:①设![]() ,若
,若![]()
![]() ,则
,则![]() ;②若偶函数
;②若偶函数![]() 在
在![]() 处可导,则
处可导,则![]() ; ③函数
; ③函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称;④函数
对称;④函数![]() 的最小值是 5.则其中错误的命题的序号是 .
的最小值是 5.则其中错误的命题的序号是 .
三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
17、(本小题满分12分)
已知定义在R上的函数f(x)=(sinωx+acosωx)(a∈R,0<ω≤1)满足:f(x)=f(-x),f(x-π)=f(x+π).
(I)求f(x)的解析式;
(II)若m2-4n>0,m,n∈R,求证:“|m|+|n|<1”是“方程[f(x)]2+mf(x)+n=0在区间(-,)内有两个不等的实根”的充分不必要条件.
18、(本小题满分12分)
下表是某班英语及数学成绩的分布表,已知该班有50名学生,成绩分1至5个档次。如表中所示英语成绩为4分,数学成绩为2分的学生有5人,现设该班任意一位学生的英语成绩为![]() ,数学成绩为
,数学成绩为![]()
|
| 数学 | |||||
| 5 | 4 | 3 | 2 | 1 | ||
| 英语 | 5 | 1 | 3 | 1 | 0 | 1 |
| 4 | 1 | 0 | 7 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 9 | 3 | |
| 2 | 1 |
| 6 | 0 |
| |
| 1 | 0 | 0 | 1 | 1 | 3 | |
(1)求![]() 的概率;(2)求在
的概率;(2)求在![]() 的条件下,
的条件下,![]() 的概率;
的概率;
(3)求![]() 的值,并求
的值,并求![]() 的数学期望;
的数学期望;
(4)若![]() 与
与![]() 是相互独立的,求
是相互独立的,求![]() 的值;
的值;
19、(本小题满分12分)
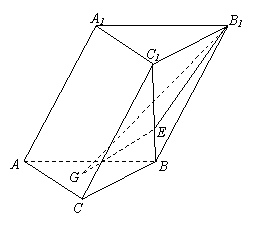 如图,在斜三棱柱
如图,在斜三棱柱![]() 中,侧面
中,侧面![]() ⊥底面
⊥底面![]() ,侧棱
,侧棱![]() 与底面
与底面![]() 成60°的角,
成60°的角,![]() ,底面
,底面![]() 是边长为2的正三角形,其重心为
是边长为2的正三角形,其重心为![]() 点.
点.![]() 是线段
是线段![]() 上一点,且
上一点,且![]() .
.
⑴求证:![]() ∥侧面
∥侧面![]() ;
;
⑵求平面![]() 与底面
与底面![]() 所成锐角二面角的大小.
所成锐角二面角的大小.
20、(本小题满分12分)
已知数列{an}满足:a1=-,![]() +(an+1+2)an+2an+1+1=0。求证:
+(an+1+2)an+2an+1+1=0。求证:
(1)-1<an<0;
(2)a2n>a2n-1对一切n∈N*都成立;
(3)数列{ a2n-1}为递增数列.
21、(本小题满分14分)
已知F1(-2,0),F2(2,0)是椭圆C的两个焦点,过F1的直线与椭圆C的两个交点为M,N,且 MN 的最小值为6.
(I)求椭圆C的方程;
(II)设A,B为椭圆C的长轴顶点.当MN取最小值时,求∠AMB的大小.
22、(本小题满分12分)
设函数![]() (a、b、c、d∈R)图象关于原点对称,且x=1时,
(a、b、c、d∈R)图象关于原点对称,且x=1时,![]() 取极小值
取极小值![]()
(1)求a、b、c、d的值;
(2)当![]() 时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;
时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;
(3)若![]() 时,求证:
时,求证:![]() .
.
座位号:
![]()
 昆明一中2005—2006学年度上学期期末高三一轮复习终结测试
昆明一中2005—2006学年度上学期期末高三一轮复习终结测试
数学试卷(理科)答题卷 2006.1
第Ⅱ卷(非选择题,共90分)
| 题号 | 二 | 三 | 合计 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 得分 | ||||||||
二、填空题(本大题共4小题,每小题4分,共16分。把答案填在答题卡相应位置。)
| 得分 | 评卷人 |
13 14
15 16
三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
| 得分 | 评卷人 |
17、(本小题满分12分)
| 得分 | 评卷人 |
18、(本小题满分12分)
| 得分 | 评卷人 |
19、(本小题满分12分)
| 得分 | 评卷人 |
20、(本小题满分12分)
| 得分 | 评卷人 |
21、(本小题满分12分)
| 得分 | 评卷人 |
22、(本小题满分12分)
昆明一中2005—2006学年度上学期期末高三一轮复习终结测试
数学试卷(理科)参考答案及评分标准 2006.1
一、选择题:(每小题5分,满分60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | A | C | B | B | D | A | C | A | C | A | B |
二、填空题:(每小题4分,满分16分)
13、2
14、f(n)=n2-1
15、![]() 16、③
16、③
三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
17、解:(I)由f(x-π)=f(x+π)知f(x)=f(x+2π),即函数f(x)的周期为2π.
∵ f(x)=(sinωx+acosωx)=sin(ωx+j),其中sinj=,cosj=,
∴ ≤2π,即ω≥1.又0<ω≤1,∴ ω=1.
又∵ f(x)=f(-x),∴ f(0)=f(),
即 (sin0+acos0)=(sin+acos),解得 a=,∴ f(x)=sin(x+).
(II)显然,x∈(-,)等价于x+∈(-,).
令u=x+,f(x)=t,g(t)=t2+mt+n,则f(x)=sinu,
由|m|+|n|<1得|m+n|≤|m|+|n|<1,∴ m+n>-1.
同理由|m-n|≤|m|+|n|<1得m-n<1.
∴ g(1)=m+n+1>0,g(-1)=1-m+n>0.
又∵|m|≤|m|+|n|<1,∴-∈(-1,1).
又∵Δ=m2-4n>0,∴ 一元二次方程t2+mt+n=0在区间(-1,1)内有两个不等的实根.
∵ 函数y=sinu(u∈(-,))与u=x+(x∈(-,))都是增函数,
∴ [f(x)]2+mf(x)+n=0在区间(-,)内有两个不等实根.
∴ “|m|+|n|<1”是“方程[f(x)]2+mf(x)+n=0在区间(-,)内有两个不等实根”的充分条件.
令m=,n=,由于方程t2+t+=0有两个不等的实根-,-,且-,-∈(-1,1),
∴ 方程sin2(x+)+sin(x+)+=0在(-,)内有两个不等的实根,
但 |m|+|n|=+=1,
故“|m|+|n|<1”不是“方程[f(x)]2+mf(x)+n=0在区间(-,)内有两个不等实根”的必要条件.
综上,“|m|+|n|<1”是“方程[f(x)]2+mf(x)+n=0在区间(-,)内有两个不等实根”的充分不必要条件.
18、解(1)由表知英语4分,数学3分的学生有7人,总学生数是50人,
![]() 所求概率为
所求概率为![]() ;
3分
;
3分
(2)![]() 的条件下,即从英语成绩在3分及3分以上的学生为总体,总体数35人,又
的条件下,即从英语成绩在3分及3分以上的学生为总体,总体数35人,又![]() 的学生为
的学生为![]() 人,
人,![]() 所求概率为
所求概率为![]() ; 6分
; 6分
(3)![]()
![]() ;
9分
;
9分
(4)![]() 与
与![]() 相互独立
相互独立![]()
![]() ;又
;又![]() 12分
12分
19、⑴延长![]() 交
交![]() 于
于![]() ,
,![]() ,
,
![]() 从而F为BC的中点.
---------------------------(2分)
从而F为BC的中点.
---------------------------(2分)
![]() 为
为![]() 的重心,
的重心,![]() ,
,![]() 三点共线,且
三点共线,且![]()
![]()
又![]()
![]() 侧面
侧面![]() ,
,![]()
![]() 侧面
侧面![]() .
--------------------(6分)
.
--------------------(6分)
⑵在侧面![]() 内,过
内,过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
![]() 侧面
侧面![]()
![]() 底面
底面![]() ,
,![]() 底面
底面![]() .
.
又侧棱![]() 与底面
与底面![]() 成
成![]() 的角,
的角,![]() =2,
=2,![]() .
.
在底面![]() 内,过
内,过![]() 作
作![]() 垂足为T,连
垂足为T,连![]() ,由三垂线定理有
,由三垂线定理有![]() ,
,
又平面![]() 与底面
与底面![]() 的交线为
的交线为![]() ,
,
![]() 为所求二面角的平面角
---------------------------------------(9分)
为所求二面角的平面角
---------------------------------------(9分)
![]()
![]() 在
在![]() 中,
中,![]()
从而平面![]() 与底面
与底面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() .
-------(12分)
.
-------(12分)
20、那么当n=k+1时,ak+1=-(ak+2)-+2。
∵1<ak+2<2,又y=t+在t∈(1,2)为增函数,
∴ak+2+∈(2,),∴ak+1∈(-,0),则-1<ak+1<0,
∴当n=k+1时结论成立。
由①②知对一切n∈N*均有-1<an<0。…………………………………3分
⑵①当n=1时,a2=->a1=-成立;
②假设当n=k时结论成立,即a2k>a2k-1,
∴1<a2k-1+2<a2k+2<2,
∴a2k-1+2+<a2k+2+,∴-a2k-1->-a2k-即a2k>a2k+1。
同上法可得a2k+2>a2k+1,
∴当n=k+1时结论成立。
由①②知对一切n∈N*均有a2n>a2n-1成立。…………………………………6分
由⑴知当x>0时,(1+x)n>1+nx,故2n+1=(1+1)n+1>1+n+1=n+2,
∴x0<1,∴0< x0<1。…………………………………………………………………9分
⑶∵an+1+an =-,则an+2+an+1=-。
两式相减得an+2-an =-=。
若把上式中n换成2n-1,
∴a2n+1-a2n-1=>0,
∴数列{ a2n-1}为递增数列。……………………………………………………………12分
21、解:(Ⅰ)由题意,设椭圆C的方程为+=1(a>b>0),其中c=2,a2-b2=4.
设M(x1,y1),N(x2,y2). 1分
若直线MN⊥x轴,则MN的方程为x=-2,代入+=1,得y2=b2(1-)=,
∴ y1-y2=,即AB=. 4分
若直线MN不与x轴垂直,则设MN的方程为y=k(x+2),代入+=1,
得 +=1,
即 (a2k2+b2)x2+4a2k2x+a2(4k2-b2)=0.
△=(4a2k2)2-4(a2k2+b2)a2(4k2-b2)=4a2b2[(a2-4)k2+b2]=4a2b4(1+k2),
∴ x1-x2=,
∴ MN=·==·>.8分
综上,MN的最小值为.由题知 =6,即 b2=3a.
代入a2-b2=4,得a2-3a-4=0,解得a=-1(舍),或a=4.∴ b2=12.
∴ 椭圆C的方程为+=1. 10分
(Ⅱ)由(Ⅰ)知A(-4,0),B(4,0).当MN取得最小值时,MN⊥x轴.
根据椭圆的对称性,不妨取M(-2,3),∠AMB即直线AM到直线MB的角.
∵ AM的斜率k1==,BM的斜率k2==-, 12分
∴ tan∠AMB===-8.
∵ ∠AMB∈(0,π),∴ ∠AMB=π-arctan8. 14分
22、解(1)∵函数![]() 图象关于原点对称,∴对任意实数
图象关于原点对称,∴对任意实数![]() ,
,
![]() ,即
,即![]() 恒成立
恒成立
![]() 2分
2分
![]() ,
,
![]() 时,
时,![]() 取极小值
取极小值![]() ,解得
,解得![]() 4分
4分
(2)当![]() 时,图象上不存在这样的两点使结论成立.
时,图象上不存在这样的两点使结论成立.
假设图象上存在两点![]() 、
、![]() ,使得过此两点处的切线互相垂直,
,使得过此两点处的切线互相垂直,
则由![]() 知两点处的切线斜率分别为
知两点处的切线斜率分别为![]() ,
,
且![]() (
*)
6分
(
*)
6分
![]() 、
、![]() ,
,![]()
此与(*)相矛盾,故假设不成立. 8分
证明(3)![]() ,
,
或![]() ,
,
![]() 上是减函数,且
上是减函数,且![]() 10分
10分
∴在[-1,1]上,![]() 时,
时,
![]() . 12分
. 12分