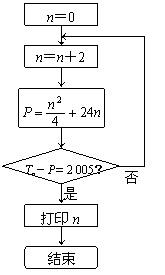襄樊市高中调研测试题(2006.1)

命题人：郭仁俊

高三数学(文史类)

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页，第Ⅱ卷3至4页，共150分，考试时间120分钟．

第 Ⅰ 卷 (选择题，共60分)

注意事项：

1．请考生将自己的学校、班级、姓名、考号填写在答题卷密封栏内，同时请认真阅读答题卷上的注意事项．

2．每小题选出答案后用2B铅笔把答题卷上对应题目的答案代号涂黑，如需改动，必须用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．

3．考试结束后，监考人员将本试卷和答题卷一并收回．

一．选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)

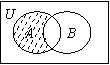
1.　　　设U为全集，集合A，B是其子集，则图中阴影部分表示的集合为
　　A．∁_UB　　　　　　　B．∁_UB
　　C．∁_UB　　　　　　　　　　 D．∁_UA∁_UB

2.　　　已知向量，，，，且，则实数x的值等于
　　A．　　　　　　　　　　B．　　　　　　　　　　 C．　　　　　　　　　　　 D．

3.　　　已知a，b，c满足c＜b＜a，且ac＜0，则下列选项中不一定能成立的是
　　A．ab＞ac　　　　　　　　 B．c (b－a)＞0　　　　　C．cb²＜ca²　　　　　　　 D．ac (a－c)＜0

4.　　　若一个600°的角的终边上有一点P(－4，)，则a的值为
　  A．　　　　　　　　　B．　　　　　　　　 C．　　　　　　　　 D．

5.　　f (x)是定义在R上的奇函数，它的最小正周期为T，则的值为
　　A．　　　　　　　　　　B．　　　　　　　　　　　 C．0　　　　　　　　　　　　　D．T

6.　　　若角和的始边都是x轴的正半轴，则是两角终边互为反向延长线的
　　A．充分不必要条件　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．必要不充分条件
　　C．充要条件　　　　　　　　　　　　　　　　　　　　　　 D．既不充分也不必要条件

7.　　　已知f (x)的定义域是(－∞，＋∞)，且f (x)是奇函数；若当x＜0时，，则的值等于
　　A．2　　　　　　　　　　　　　B．　　　　　　　　　　　 C．－2　　　　　　　　　　　D．

8.　　的值
　　A．小于零　　　　　　　　B．大于零　　　　　　　　C．等于零　　　　　　　　D．不确定

9.　　　曲线和直线在y轴右侧的交点按横坐标从小到大依次记为P₁，P₂，P₃，…，则｜P₂P₄｜等于
　　A．　　　　　　　　　　　B．2　　　　　　　　　　　C．3　　　　　　　　　　　D．4

10.　 若指数函数 (a＞0且a≠1)满足，则不等式＜0的解集为
　　A．(－1，1)　　　　　　　 B．(－1，0)　　　　　　　 C．(0，1)　　　　　　　　　D．(－1，0)∪(0，1)

11.　 已知等比数列{a_n}的首项为8，S_n是其前n项的和，某同学经计算得S₂ = 20，S₃ = 36，S₄ = 65，后来该同学发现了其中一个数算错了，则该数为
　　A．S₁　　　　　　　　　　　　 B．S₂　　　　　　　　　　　　 C．S₃　　　　　　　　　　　　 D．S₄

12.　 某文具用品店出售羽毛球拍和羽毛球，球拍每副定价20元，羽毛球每只定价5元，该店制定了两种优惠方法：①买一副球拍赠送一只羽毛球；②按总价的92%付款．某人计划购买4副球拍，30只羽毛球，两种优惠方法中，哪一种更好？
　　A．①　　　　　　　　　　　 B．②　　　　　　　　　　　　C．①②同样好　　　　D．不能确定

第 Ⅱ 卷 (非选择题，共90分)

注意事项：

第Ⅱ卷共2页，用黑色签字笔直接答在答题卷每题对应的答题区域内；如需改动，先划掉原来的答案，然后写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．

二．填空题(本大题共4小题，每小题4分，共16分．将正确答案填在答题卷上对应题号的横线上)

13. 已知集合P = {(x，y)｜y = m}，Q = {(x，y)｜y = ，a＞0，a≠1}，如果有且只有一个元素，那么实数m的取值范围是　▲　．

14. 函数图象恒过定点(0，1)，若存在反函数，则的图象必过定点　▲　．

15. 函数在区间(1，+∞)上是单调增函数，则a的取值范围是　▲　．

16. 已知函数，[-2，2]表示的曲线过原点，且在x = ±1处的切线斜率均为－1，则f (x)的解析式为f (x) = 　▲　．

三．解答题(本大题共6小题，满分74分．解答应写出文字说明，证明过程或演算步骤)

17. (本大题满分12分)已知关于x的不等式的解集为M．
　　(1)当a = 4时，求集合M；
　　(2)若3M且5M，求实数a的取值范围．

18. (本大题满分12分)已知，1)，，0)，其中＞0，又函数f (x) 是以为最小正周期的周期函数，当x∈[0，]时，函数f (x)的最小值为－2．
　　(1)求f (x)的解析式；
　　(2)写出函数f (x)的单调递增区间；
　　(3)将函数f (x)的图象沿向量m平移后可以得到一个偶函数的图象，请写出一个符合条件的向量m．

19.  (本大题满分12分)数列{a_n}的前n项和为S_n，已知．
　　(1)求数列{a_n}的通项公式；
　　(2)若数列{c_n}满足，数列{c_n}的前n项和为T_n，当n为偶数时，求T_n；
　　(3)张三同学利用第(2)题中的T_n设计了一个程序流程如图，但李四同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去，而无法结束)．你是否同意李四同学的观点？请说明理由．

20. (本大题满分12分)从4月1日开始，有一新款服装投入某商场销售，4月1日该款服装销售出20件，第二天销售出25件，第三天销售出40件，以后，每天售出的件数分别递增15件，直到4月12号日销售量达到最大，然后，每天销售的件数分别递减10件．
　　(1)记该款服装四月份日销售量与销售天数n的关系为a_n，求a_n；
　　(2)求四月份的总销售量；
　　(3)按规律，当该商场销售此服装超过1 300件时，社会上就流行，而日销售量连续下降，且日销售量低于100件时，则流行消失，问：该款服装在社会上流行是否超过10天？说明理由．

21. (本大题满分12分)已知是定义在R上的不恒为0的函数，且对于任意a、b∈R都满足：．
　　(1)求、的值；
　　(2)判断的奇偶性并证明你的结论；
　　(3)若， (n＞0，n∈N)，求数列{b_n}的前n项和．

22. (本大题满分14分)如图，曲线段OMB是函数f (x) = x² (0＜x＜6)的图象，BA⊥x轴于A，曲线段OMB上一点M (t，t ² )处的切线PQ交轴于点P，交线段AB于点Q．
　　(1)试用t表示切线PQ的方程；
　　(2)设△QAP的面积为g (t)，若函数g (t)在(m，n)上单调递减，试求出m的最小值；
　　(3)求函数g (t)的值域．