扬州市2005~2006学年度第二学期调研测试
高三数学试题
注意事项：本试卷共4页，满分150分，考试时间120分钟．
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）．
1．
设集合
，
，若
，则
等于
A．
B．
C．
D．
2．
若平面向量
与
的夹角是
，且
，则等于
A．
B．
C．
D．
3． 已知等差数列
的公差为2，且
成等比数列，则
等于
A．
B．
C．
D．
4．
函数
的递减区间是
A．
B．
C．
D．
5．
已知
、
表示不同的平面，
、
表示不同的直线，则下列命题中不正确的是
A．若⊥，
，则
B．
，
，则
C．若
，
，则 D．若⊥，⊥，则
6．
若
，则“
”是“方程
表示双曲线”的
A．充分不必要条件 B． 必要不充分条件
C．充要条件 D． 既不充分又不必要条件
7．
在球面上有A、B、C三点，如果
cm，且球心O到平面ABC的距离是3 cm，则球的表面积是
A．
cm2 B．
cm2
C．
cm2 D．
cm2
8．
已知抛物线
：
与抛物线
关于直线
对称，则的准线方程是
A．
B．
C． 
D． 
9．
函数
的图象沿向量平移可得函数
的图象，则为
A．
B．
C．
D．
10． 在6张卡片上分别写上数字0，1，2，3，4，5，然后把它们混合，再任意排成一行，组成最高位不为0的6位数，则能被5整除的概率为
A．0.2 B．0.3 C．0.36 D．0.46
11．
设函数
有性质：①
；②
；③
；④
．
则在下面所给四个函数中，能同时满足以上三个性质的函数是
A．
B．
C．
D．
12． 通讯中常采取重复发送信号的方法来减少在接受中可能发生的错误．假定发报机只发0和1两种信号，接受时发生错误是0接受为1或1接受为0，它们发生的概率都是0．1，为减少错误，采取每一种信号连发3次，接受时以“少数服从多数”的原则判断，则判错一个信号的概率为
A．
B．
C．
D．
二、填空题（本大题共6小题，每小题4分，共24分）
13．
函数
的反函数是 ☆ ．
14．
在条件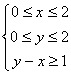
下， 
的最大值是 ☆ ．
15．
圆
在点
处的切线方程为
☆ ．
16． 正三棱锥的侧面均为直角三角形，则它的侧面与底面所成角的余弦值是 ☆ ．
17．
已知数列满足递推关系式
，
，且
为等差数列，则
的值是 ☆ ．
18． 假设要考察某公司生产的500克袋装牛奶的质量是否达标，现从800袋牛奶中抽取60袋进行检验，利用随机数表抽取样本时，先将800袋牛奶按000，001，…，799进行编号，如果从随机数表第8行第18列的数开始向右读，请你依次写出最先检测的5袋牛奶的编号 ☆ ．（下面摘取了一随机数表的第7行至第9行）
……
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 62 58 79
73 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
……
三、解答题（本大题共5小题，共66分.解答应写出必要的文字说明，证明过程或演算步骤）.
19． （本题满分12分）
数列的前项和记为
，数列
是首项为2，公比也为2的等比数列．
（Ⅰ）求
；
（Ⅱ）若数列
的前项和不小于100，问此数列最少有多少项？
20． （本题满分12分）
如图，摩天轮的半径为40ｍ，点O距地面的高度为50ｍ，摩天轮做匀速转动，每3min转一圈，摩天轮上的点P的起始位置在最低点处．
（Ⅰ）已知在时刻
（min）时点P距离地面的高度
，求2006min时点P距离地面的高度；
（Ⅱ）求证：不论为何值，
是定值．
21． （本题满分14分）
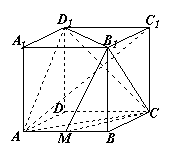
如图，正方体ABCD—A1B1C1D1的棱长为1， M是棱AB的中点．
（Ⅰ）求CD与平面AC D1所成的角；
（Ⅱ）求证：平面B1C D1⊥平面B1CM；
（Ⅲ）求点A1到平面B1CM 的距离．
22． （本题满分14分）
已知P是椭圆C：
上异于长轴端点的任意一点，A为长轴的左端点，F为椭圆的右焦点，椭圆的右准线与x轴、直线AP分别交于点K、M，
．
（Ⅰ）若椭圆的焦距为6，求椭圆C的方程；
（Ⅱ）若
，求证：
．
23． （本题满分14分）
已知函数
，
，
的最小值恰好是方程
的三个根，其中
．
（Ⅰ）求证：
；
（Ⅱ）设
，
是函数
的两个极值点．
①若
，求函数的解析式；
②求
的取值范围．