试卷类型 A
襄樊市高中调研测试题
高三数学(文史类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分，考试时间120分钟．
第 Ⅰ 卷 (选择题，共60分)
注意事项：
1．请考生将自己的考号、姓名填写在第Ⅱ卷密封线内．
2．每小题选出答案后填写在第Ⅱ卷前的答题栏内对应题号下面，不能答在试题卷上．
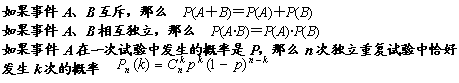参考公式：
一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 设实数集R为全集，集合P＝{x｜f (x)＝0}，Q＝{x｜g (x)＝0}，H＝{x｜h(x)＝0}，则方程
的解集是
A．
∁RH B．
∁RH C．
D．
2.
在等差数列{an}中，若a4＋a6＋a8＋a10＋a12＝120，则2 a10－a12的值为
A．20 B．22 C．24 D．28
3.
函数
的奇偶性是
A．是奇函数不是偶函数 B．是偶函数不是奇函数
C．既是奇函数又是偶函数 D．既不是奇函数也不是偶函数
4.
设O是平面上任意一点，
＝a，
＝b，
＝ma＋nb (m、n∈R)，若A、B、C三点共线，则m、n满足
A．m＋n＝－1 B．m＋n＝1 C．m＋n＝0 D．m－n＝1
5.
要使
有意义，则m范围是
A．m≤
B．m≥－1
C．m≤－1或m≥ D．－1≤m≤
6.
设P＝1＋5(x＋1)＋10 (x＋1)2＋10(x＋1) 3＋5(x＋1) 4＋(x＋1) 5，则P等于
A．x5 B．(x＋2)5 C．(x－1) 5 D．(x＋1) 5
7.
若a、b∈R，则下列不等式：①a2＋3＞2a；②a2+b2≥2(a－b－1)；③a5＋b5＞a3b2＋a2b3；④a＋
≥2．其中一定成立是
A．①②③ B．①②④ C．①② D．②④
8.
若函数f (x)的定义域为(0，＋∞)，且f (x)＞0，f / (x)＞0，那么函数y＝xf (x)
A．存在极大值 B．存在极小值 C．是增函数 D．是减函数
|
|
9.
已知函数
的反函数是
，则函数
的图象是
A B C D
10. 在6个电子产品中，有两个次品，4个合格品，每次任取一个测试，测试完后不放回，直到两个次品都找到为止，那么经过四次测试恰好将两个次品全部找出来的概率是
A．
B．
C．
D．
11. 直线y＝m(m为常数)与正切曲线y＝
(
＞0)相交，则相邻两个交点的距离是
A．
B．
C．
D．
12. 若函数
的图象与x轴有公共点，则m的取值范围是
A．m≤－1 B．－1≤m＜0 C．m≥1 D．0＜m≤1
第Ⅰ卷答题栏
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||||
[ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | ||||
[ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | ||||
[ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | ||||
| [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] |
襄樊市高中调研测试题(2005.1)
高三数学(文史类)
第 Ⅱ 卷 (非选择题，共90分)
注意事项：
第Ⅱ卷共6页，用黑色签字笔直接答在试题卷中，答卷前将密封线内的项目填写清楚．
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得 分 | |||||||||
| 得分 | 评卷人 |
二．填空题：本大题共4小题，每小题4分，共16分．将正确答案填在题中横线上．
13.
若sin2α＜0，sin α－cos α＞0，则cos α
＋sin α
＝ ．
14.
不等式
对一切实数x都成立，则a的取值范围是 ．
15. 采用简单随机抽样从个体数为6的总体中抽取一个容量为3的样本，则每个个体被抽到的概率为 ．
16.
设
是函数
的反函数，若
，则f (a＋b)的值为 ．
三．解答题：本大题共6小题，满分74分．
| 得分 | 评卷人 |
| 得分 | 评卷人 |
17.
(本大题满分12分) 已知函数
．
(1) 将f (x)写成
+C的形式，并求其图象对称中心的横坐标；
(2) 如果△ABC的三边a、b、c满足b2＝ac，且边b所对的角为x，试求x的范围及此时函数f (x)的值域．
18.
(本大题满分12分)集合A是由适合以下性质的函数
组成的：对于任意的x≥0， f (x)∈[－2，4]，且f (x)在[0，＋∞)上是增函数．
(1)判断函数
及
(x≥0)是否在集合A中？并说明理由．
(2)对于(1)中你认为是集合A中的函数f (x)，不等式f (x)＋ f (x＋2)＜2 f (x＋1)是否对于任意的x≥0总成立？证明你的结论．
19.
(本大题满分12分) 设向量a＝(
，－1) ，b＝( 
，
)，若存在实数m (m≠0)和角
，使c＝a＋(tan2θ－3)b，d＝－ma＋(tanθ)b，且c⊥d．
(1)试求函数m＝f (θ)的关系式；
(2)求函数m＝f (θ)的最大值和最小值．
| 得分 | 评卷人 |
20.
(本大题满分12分) 某售货员负责在甲、乙、丙三个柜面上售货，如果在某一个小时内各柜面不需要售货员照顾的概率分别为0.9、0.8、0.7．假定各个柜面是否需要照顾相互之间没有影响，求在这个小时内：
(1)只有丙柜面需要售货员照顾的概率；
(2)三个柜面最多有一个需要售货员照顾的概率；
(3)三个柜面至少有一个需要售货员照顾的概率．
| 得分 | 评卷人 |
21.
(本大题满分12分)已知函数f (x)满足f ( xy)＝f (x)
f (y) (x、y∈R)，且
x＞1时，f (x)＜1，又
．
(1)求证：当x＞0时，f (x)＞0；
(2)求证：f (x)在(0，＋∞)上的单调递减；
(3)解关于x的不等式：
＞1．
| 得分 | 评卷人 |
22.
(本大题满分14分)已知一次函数f (x)的图象关于y＝x对称的图象为C，且f (1)＝0，若点
(
N*)在曲线C上，a1＝1，对于不小于2的任意正整数n，都有
．
(1) 求曲线C 的方程；
(2) 求{an}的通项公式；
(3) 设
，求Sn．
| 得分 | 评卷人 |
高三数学(文史类)参考答案及评分标准
说明：
1．本解答指出了每道题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．
2．对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．
3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．
4．只给整数分数，选择题和填空题不给中间分数．
一．选择题：BCBBD BCCCA BB
二．填空题：13．
14．(
，＋∞) 15． 16．2
三．解答题：
17．解：(1) 
2分
4分
由
得：
(k∈Z)
∴对称中心的横坐标为
(k∈Z)． 6分
(2)由已知得
≥ 8分
又x是△ABC的内角，
∴x的取值范围是
10分
这时，
，∴
≤1
故函数f (x)的值域是
． 12分
18．解：(1) 函数
不在集合A中
∵当x＝49时，f (49)＝5＞4，不满足条件 4分
∵当x≥0时，0＜
≤1，∴－2≤
＜4
即f2 (x)∈[－2，4]， 6分
又设x1＜x2，则
， 
， Þ f2 (x1)＜f2 (x2)
即f2 (x)是增函数，∴f2 (x)在集合A中． 8分
(2)
∴不等式f (x)＋ f (x＋2)＜2 f (x＋1)对于任意的x≥0总成立． 12分
19．解：(1)a·b＝
∴c·d＝[a＋(
－3)b][－ma＋(
)b]＝－ma2＋(
)b2 4分
∵c⊥d，∴c·d＝0，即－ma2＋()b2＝0，
又 a
＝2， b ＝1
∴m＝
，其中
6分
(2)令tan θ＝t，得m＝g (t)＝
(t3－3t)，t∈[－1，1]
求导得 g
/(t )＝(t2－1)≤0 8分
g (t)在[－1，1]上单调递减 10分
∴当t＝－1，即
时，函数g (t)有最大值，当t＝1，即
时，函数g (t)有最小值－． 12分
20．解：设事件A为“甲柜面不需要售货员照顾”，事件B为“乙柜面不需要售货员照顾”，事件C为“丙柜面不需要售货员照顾”
则事件A、B、C相互独立，且P(A)＝0.9，P(B)＝0.8，P(C)＝0.7． 2分
(1)设事件D表示“某一小时内只有丙柜面需要售货员照顾”，则
，且事件A、B、
相互独立
∴P(D)＝P(
)＝P(A)
P(B) P()＝0.9×0.8×0.3＝0.216． 4分
(2) 设事件E表示“某一小时内三个柜面最多有一个需要售货员照顾”，
则
6分
又
彼此互斥，且A、B、C、
相互独立
∴
= 0.9×0.8×0.7＋0.1×0.8×0.7＋0.9×0.2×0.7＋0.9×0.8×0.3＝0.902 8分
(3) 设事件F表示“某一小时内三个柜面至少有一个需要售货员照顾”，
则
10分
又A、B、C相互独立
∴
＝P(A)
P(B) P(C)＝0.9×0.8×0.7＝0.504
∴
＝0.496． 12分
21．解：(1)∵x＞0，∴
≥0
又若
，则
，与矛盾
∴f (x)＞0． 4分
(2)设0＜x1＜x2，则
＞1，∴0＜
＜1
∴
∵f (x1)＞0，0＜＜1，∴f (x1)＜ f (x2)
故f (x)在(0，＋∞)上是减函数． 8分
(3) 由f (xy)＝f (x)f (y)得：f (1)＝f (1×1)＝f (1)f
(1)＝[f (1)]2
由(1)知f (1)＞0，∴f (1)＝1
不等式可化为：
由(2)可得：
10分
两边平方得：2ax―a2＜0，
当a＜0时，解得
，
当a＞0时，解得
，
当a＝0时，不等式化为：0＜0，无解．
综上所述，当a＝0，不等式的解集是
，当a＜0时，不等式的解集是{x｜
}，当a＞0时，不等式的解集是{x｜}． 12分
22．解：(1)设f (x)＝ax＋b(a≠０)，则a＋b＝０
∴曲线C的方程为
∵点
(N*)在曲线C上，∴
2分
由
知{
}是公差为１的等差数列，
∴
4分
∴
Þ a＝１
∴曲线C的方程为y＝x＋１． 6分
(2)由(1)得：
∴
8分
相乘得：
即
Þ an＝n！ 10分
(3)
12分
∴
14分．