试卷类型 A
襄樊市高三调研测试题
数 学(理工农医类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至4页,共150分,考试时间120分钟.
第 Ⅰ 卷(选择题,共60分)
注意事项:
1.答卷前,请考生将自己的学校、班级、姓名、准考证号填写在答题卷密封线内.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试题卷上无效.
3.考试结束后,监考人员将本试卷和答题卷一并收回.

 参考公式
参考公式
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
若非空数集A = {x|2a +
1≤x≤3a-5 },B = {x|3≤x≤22 },则能使![]() 成立的所有a的集合是
成立的所有a的集合是
A.{a|1≤a≤9} B.{a|6≤a≤9} C.{a|a≤9} D.![]()
2.
不等式![]() 的解集是
的解集是
A.{x︱x>![]() } B.{x︱x<
} B.{x︱x<![]() }
}
C.{x︱![]() <x<1或x>1} D.{x|x<
<x<1或x>1} D.{x|x<![]() 或x>1}
或x>1}
3.
若点P(3,4)、Q(a,b)关于直线![]() 对称,则
对称,则
A.a = 1,b =![]() B.a = 2,b
=
B.a = 2,b
= ![]() C.a = 4,b
= 3 D.a = 5,b
= 2
C.a = 4,b
= 3 D.a = 5,b
= 2
4.
若复数z满足![]() 和
和![]() ,则z的值为
,则z的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.
已知直线m、n,平面![]() ,则
,则![]() 的一个充分不必要条件为
的一个充分不必要条件为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.
抛物线![]() 按向量e 平移后的焦点坐标为 (3,2),则平移后的抛物线顶点坐标为
按向量e 平移后的焦点坐标为 (3,2),则平移后的抛物线顶点坐标为
A.(4,2) B.(2,2) C.(-2,-2) D.(2,3)
7.
设a、b、c∈R*,那么三个数![]() 、
、![]() 、
、![]()
A.都不大于2 B.都不小于2
C.至少有一个不大于2 D.至少有一个不小于2
8.
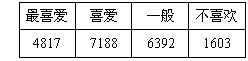 某电视台在因特网上就观众对其某一节目的喜爱程度进行调查,参加调查的人数为20000人,其中持各种态度的人数如右表所示.电视台为了了解观众的具体想法和意见,打算从中抽选出100人进行更为详细的调查,为此要进行分层抽样,那么在分层抽样时,每类人中各应抽选出的人数近似为
某电视台在因特网上就观众对其某一节目的喜爱程度进行调查,参加调查的人数为20000人,其中持各种态度的人数如右表所示.电视台为了了解观众的具体想法和意见,打算从中抽选出100人进行更为详细的调查,为此要进行分层抽样,那么在分层抽样时,每类人中各应抽选出的人数近似为
A.25,25,25,25 B.24,36,32,8
C.20,40,30,10 D.48,72,64,16
9.
点P在直径为![]() 的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是
的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是
A.![]() B.6 C.
B.6 C.![]() D.
D.![]()
10.  已知函数
已知函数![]() 在区间(
在区间(![]() ,1)上有最小值,则函数
,1)上有最小值,则函数![]() 在区间(1,
在区间(1,![]() 上一定
上一定
A.有最小值 B.有最大值 C.是减函数 D.是增函数
|
|
11. 已知函数f (x)的定义域为[a,b],函数f (x)的图象如右图所示,则函数f ( x )的图象是
12. 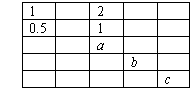 在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵行成等比数列,则a+b+c的值为
在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵行成等比数列,则a+b+c的值为
A.1 B.2
C.3 D.4
第 Ⅱ 卷(非选择题,共90分)
注意事项:
第Ⅱ卷共2页,用黑色签字笔直接答在答题卷每题对应的答题区域内;如需改动,先划掉原来的答案,然后写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
二.填空题:本大题共4小题,每小题4分,共16分.将正确答案填在答题卷上对应题号的横线上.
13. 已知e1、e2是两个不共线的向量,a = k2e1
+ (![]() k)e2和b = 2e1 + 3e2是两个共线向量,则实数k = .
k)e2和b = 2e1 + 3e2是两个共线向量,则实数k = .
14.
若![]() …
…![]() ,则
,则![]() …
…![]()
![]() .
.
15.
 将大小不同的两种钢板截成A、B两种规格的成品,每张钢板可同时截得这两种规格的成品的块数如右表所示.现在需要A、B两种规格的成品分别为12块和10块,则至少需要这两种钢板共 张.
将大小不同的两种钢板截成A、B两种规格的成品,每张钢板可同时截得这两种规格的成品的块数如右表所示.现在需要A、B两种规格的成品分别为12块和10块,则至少需要这两种钢板共 张.
| ○○○○○○○ |
16. 霓虹灯的一个部位由七个小灯泡组成(如右图),每个灯泡均可亮出红色或黄色.现设计每次变换只闪亮其中三个灯泡,且相邻两个不同时亮,则一共可呈现 种不同的变换形式(用数字作答).
三.解答题:本大题共6小题,满分74分.解答应写出文字说明,证明过程或演算步骤.
17.
(本大题满分12分)
已知向量a![]() ,b
,b![]() ,c = (1,0),其中
,c = (1,0),其中![]() ,
,![]() .若a与c的夹角为
.若a与c的夹角为![]() ,b与c的夹角为
,b与c的夹角为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
18. (本大题满分12分)
设一汽车在行进途中要经过4个路口,汽车在每个路口遇到绿灯的概率为![]() ,遇到红灯(禁止通行)的概率为
,遇到红灯(禁止通行)的概率为![]() .假定汽车只在遇到红灯或到达目的地才停止前进,
.假定汽车只在遇到红灯或到达目的地才停止前进,![]() 表示停车时已经通过的路口数,求:
表示停车时已经通过的路口数,求:
(1)![]() 的概率的分布列及期望E
的概率的分布列及期望E![]() ;
;
(2)停车时最多已通过3个路口的概率.
|
|
19. (本大题满分12分)
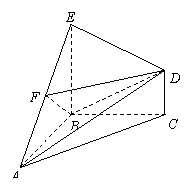
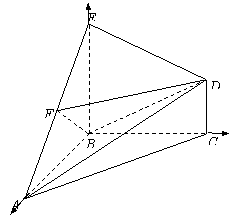
如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC = 90°,BE和CD都垂直于平面ABC,且BE = AB = 2,CD = 1,点F是AE的中点.
(1)求证:DF∥平面ABC;
(2)求AB与平面BDF所成角的大小.
20. (本大题满分12分)
已知数列{an}的各项均为正数且a1 = 6,点![]() 在抛物线
在抛物线![]() 上;数列{bn}中,点
上;数列{bn}中,点![]() 在过点(0,1)且方向向量为(1,2)的直线上.
在过点(0,1)且方向向量为(1,2)的直线上.
(1)求数列{an}、{bn}的通项公式;
(2)对任意正整数n,不等式![]() ≤
≤![]() …
…![]() 成立,求正数a的取值范围.
成立,求正数a的取值范围.
21. (本大题满分12分)
已知![]() 是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求c的值;
(2)在函数f (x)的图象上是否存在一点M(x0,y0),使得f (x)在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;
(3)求
AC 的取值范围.
22.  (本大题满分14分)
(本大题满分14分)
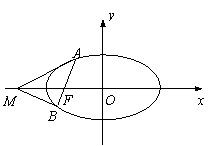
如图,过椭圆![]() 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
(1)求椭圆![]() 的“左特征点”M的坐标;
的“左特征点”M的坐标;
(2)试根据(1)中的结论猜测:椭圆![]()
![]() 的“左特征点”M是一个怎样的点?并证明你的结论.
的“左特征点”M是一个怎样的点?并证明你的结论.
数学(理工农医类)参考答案及评分标准
命题人:郭仁俊
说明:
1.本解答指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
2.对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,选择题和填空题不给中间分数.
一.选择题:BCDC CBDB DDBA
二.填空题:13.![]() 或
或![]() 14.
14.![]() 15.7 16.80
15.7 16.80
三.解答题:
17.解:
a ![]() ,
,
b ![]() ,
,
c = 1 4分
又a·c![]() ,b·c
,b·c![]()
![]() ,
,![]() 6分
6分
∵![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ,故
,故![]()
由![]() ,得
,得![]() 8分
8分
由![]() ,有
,有![]() ,∴
,∴![]() 10分
10分
∴![]() . 12分
. 12分
18.(1)解:![]() =0表示停车时已经通过0个路口,即在第一个路口遇到红灯,其概率为
=0表示停车时已经通过0个路口,即在第一个路口遇到红灯,其概率为![]()
![]() =1表示停车时已经通过1个路口,即在第一个路口遇到绿灯,在第二个路口遇到红灯,其概率为
=1表示停车时已经通过1个路口,即在第一个路口遇到绿灯,在第二个路口遇到红灯,其概率为![]()
……
得分布列如下:

6分
则![]() . 8分
. 8分
(2)解:![]() . 12分
. 12分
|
|
19.(1)解:取AB的中点G,连CG,FG,
则FG∥BE,且FG=![]() BE,
BE,
∴ FG∥CD且FG=CD, 2分
∴ 四边形FGCD是平行四边形,
∴ DF∥CG,
又∵ CG![]() 平面ABC,
平面ABC,
∴DF∥平面ABC
4分
(2)解:以点B为原点,BA、BC、BE所在的直线分别为x、y、z轴,建立空间直角坐标系,则
B(0,0,0),A(2,0,0),C(0,2,0),D(0,2,1),E(0,0,2),F(1,0,1)
∴ ![]() (0,2,1),
(0,2,1),![]() (1,-2,0) 6分
(1,-2,0) 6分
设平面BDF的一个法向量为n = (2,a,b),
∵ n⊥![]() ,n⊥
,n⊥![]() , ∴
, ∴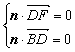 8分
8分
即![]() ,解得
,解得![]() ,
,
∴n =(2,1,-2) 10分
又设AB与平面BDF所成的角为![]() ,则法线n与
,则法线n与![]() 所成的角为
所成的角为![]() ,
,
∴ ![]() ,
,
即 ![]() ,故AB与平面BDF所成的角为arcsin
,故AB与平面BDF所成的角为arcsin![]() . 12分
. 12分
20.(1)解:将点![]() 代入
代入![]() 中得
中得
![]() 即
即![]()
∴![]() 2分
2分
过点(0,1)且方向向量为(1,2)的直线为![]()
∴![]() 4分
4分
(2) 对任意正整数n,不等式![]() ≤
≤![]() …
…![]() 成立
成立
即a≤![]() …
…![]() 对任意正整数n成立 6分
对任意正整数n成立 6分
记![]() …
…![]()
则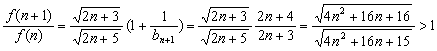 8分
8分
∴![]() ,即f (n)递增 10分
,即f (n)递增 10分
故![]() ,∴0<a≤
,∴0<a≤![]() . 12分
. 12分
21.(1)解:![]()
依题意![]() 在
在![]() 和[0,2]上有相反的单调性,
和[0,2]上有相反的单调性,
∴x = 0是f (x)的一个极值点,故![]() ,得c = 0 2分
,得c = 0 2分
(2)解:因为f (x)交x轴于点B(2,0)
∴![]() ,即
,即![]() 4分
4分
令![]() 得
得![]()
因为f (x)在[0,2]和[4,5]上有相反的单调性,∴![]() 在[0,2]和[4,5]上有相反的符号
在[0,2]和[4,5]上有相反的符号
故2≤![]() ≤4 Þ -6≤
≤4 Þ -6≤![]() ≤-3 6分
≤-3 6分
假设存在点M(x0,y0)使得f (x)在点M的切线斜率为3b,则f / (x0)
=3b,
即![]()
![]()
而-6≤![]() ≤-3,∴△<0
≤-3,∴△<0
故不存在点M(x0,y0),使得f (x)在点M的切线斜率为3b. 8分
(3)解:设![]() ,依题意可令
,依题意可令![]()
![]()
则![]() 即
即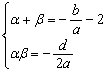 10分
10分
∴![]()
∵-6≤![]() ≤-3,∴当
≤-3,∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,故3≤
AC ≤4
,故3≤
AC ≤4![]() . 12分
. 12分
22.(1)解:设M(m,0)为椭圆![]() 的左特征点,椭圆的左焦点为
的左特征点,椭圆的左焦点为![]() ,
,
设直线AB的方程为![]()
将它代入![]() 得:
得:![]() ,即
,即![]() 2分
2分
设A(x1,y1),B(x2,y2),则![]() ,
,![]() 4分
4分
∵∠AMB被x轴平分,∴![]()
即![]() ,Þ
,Þ ![]()
Þ ![]()
∴![]() , 6分
, 6分
于是![]()
∵![]() ,∴
,∴![]() ,即
,即![]()
∴M(![]() ,0) 8分
,0) 8分
(2)解:对于椭圆![]() ,
,![]() ,b = 1,c = 2,∴
,b = 1,c = 2,∴![]() .
.
于是猜想:椭圆![]() 的“左特征点”是椭圆的左准线与x轴的交点. 10分
的“左特征点”是椭圆的左准线与x轴的交点. 10分
证明:设椭圆的左准线l与x轴相交于M点,过A、B分别作l的垂线,垂足分别为C、D
据椭圆第二定义:![]() ,即
,即![]()
∵![]() ,∴
,∴![]() 12分
12分
于是![]() ,即
,即![]()
∴![]() ,又
,又![]() 均为锐角,
均为锐角,
∴![]() ,∴
,∴![]()
∴MF为∠AMB的平分线,故M为椭圆的“左特征点”. 14分