试卷类型 A
襄樊市高三调研测试题
数 学(理工农医类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至4页,共150分,考试时间120分钟.
第 Ⅰ 卷(选择题,共60分)
注意事项:
1.答卷前,请考生将自己的学校、班级、姓名、准考证号填写在答题卷密封线内.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试题卷上无效.
3.考试结束后,监考人员将本试卷和答题卷一并收回.

 参考公式
参考公式
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
已知集合A={y|y = log2x,x>1},B={y|![]() ,x>1},则
,x>1},则![]() 等于
等于
A.{y|0<y<![]() } B.{y|0<y<1} C.{y|
} B.{y|0<y<1} C.{y|![]() <y<1} D.
<y<1} D.![]()
2.
等差数列{an}前四项和为40,末四项和为72,所有项和为140,则该数列共有
A.9项 B.12项 C.10项 D.13项
3.
不等式|x2-10|≤3x的解集为
A.{x|2≤x≤![]() } B.{x|-2≤x≤5}
} B.{x|-2≤x≤5}
C.{x|2≤x≤5} D.{x|![]() ≤x≤5}
≤x≤5}
4.
点P(2,-1)为圆 (x-1) 2+y2=25内弦AB中点,则直线AB的方程是
A.x-y-3=0 B.2x+y-3=0 C.x+y-1=0 D.2x-y-5=0
5. 椭圆![]() 上一点M到焦点F1的距离为2,N是MF1的中点,则 ON 等于
上一点M到焦点F1的距离为2,N是MF1的中点,则 ON 等于
A..2 B.4 C.6 D.![]()
6. 复数![]() 与
与![]() (a、b、c、d
(a、b、c、d![]() R)的积是纯虚数的充要条件是
R)的积是纯虚数的充要条件是
A.ac-bd=0 B.ad+bc=0
C.ac-bd≠0且ad+bc=0 D.ac-bd=0且ad+bc≠0
7.
已知向量a=(cos 15°,sin 15°),b=(-sin 15°,-cos 15°),则|a+b|的值为
A.1 B.![]() C.
C.![]() D.
D.![]()
|
|
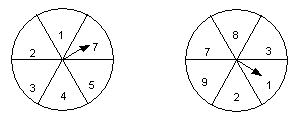
8. 如图,南北方向的公路l,A地在公路的正东2km处,B地在A地东偏北30°方向2![]() km处, 河流沿岸PQ上任一点到公路l和到A地距离相等.现要在曲线PQ上选一处M建一座码头,向A、B两地转运货物,经测算从M到A、M到B修建公路的费用均为a万元/km,那么修建这两条公路的总费用最低是
km处, 河流沿岸PQ上任一点到公路l和到A地距离相等.现要在曲线PQ上选一处M建一座码头,向A、B两地转运货物,经测算从M到A、M到B修建公路的费用均为a万元/km,那么修建这两条公路的总费用最低是
A.![]() 万元 B.
万元 B.![]() 万元
万元
C.5a万元 D.6a万元
9. 设a>b>c,n![]() N*,且
N*,且![]() ≥
≥![]() 恒成立,则n的最大值为
恒成立,则n的最大值为
A.2 B.3 C.4 D.5
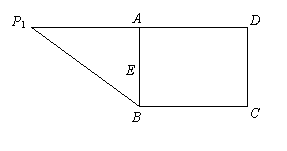
10.  如图所示,在两个圆盘中同时转动指针,当指针停止时落在本圆盘每个数所在区域的机会均等,那么当指针停止时,两个指针同时落在奇数所在区域的概率是
如图所示,在两个圆盘中同时转动指针,当指针停止时落在本圆盘每个数所在区域的机会均等,那么当指针停止时,两个指针同时落在奇数所在区域的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11. 若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y=x2,值域为{1,4}的“同族函数”共有
A.9个 B.8个 C.5个 D.4个
12. 已知函数f (x)=x3+x,且a+b>0,b+c>0,c+a>0,则y=f (a)+f (b)+f (c)的值是
A.正数 B.负数 C.零 D.正数或负数
第 Ⅱ 卷(非选择题,共90分)
注意事项:
第Ⅱ卷共2页,用黑色签字笔直接答在答题卷每题对应的答题区域内;如需改动,先划掉原来的答案,然后写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
二.填空题:本大题共4小题,每小题4分,共16分.将正确答案填在答题卷上对应题号的横线上.
13. (1-x+x2)(1+x)6展开式中,x3项的系数为 * .
14.
当![]() * 时,
* 时,![]() 在[0,2]上是减函数.
在[0,2]上是减函数.
15.
已知a、b为不垂直的异面直线,![]() 是一个平面,则a、b在
是一个平面,则a、b在![]() 上的射影有可能是:
上的射影有可能是:
①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点.
在上面结论中,正确结论的编号是 * (写出所有正确结论的编号).
|
|
16.
为了保证信息安全传输,有一种称为秘密密钥密码系统(Private Key Cryptosystem),其加密、解密原理如下图:
现在加密密钥为![]() ,如上所示,明文“6”通过加密后得到密文“3”,再发送,接受方通过解密密钥解密得到明文“6”.问:若接受方接到密文为“4”,则解密后得明文为 * .
,如上所示,明文“6”通过加密后得到密文“3”,再发送,接受方通过解密密钥解密得到明文“6”.问:若接受方接到密文为“4”,则解密后得明文为 * .
三.解答题:本大题共6小题,满分74分.解答应写出文字说明,证明过程或演算步骤.
17. (本大题满分12分)
已知向量m=(sin B,1-cos B),且与向量n=(1,0)所成角为![]() ,其中A、B、C是
,其中A、B、C是![]() ABC的内角,求
ABC的内角,求![]() 的取值范围.
的取值范围.
18. (本大题满分12分)
已知数列{an}的前n项和为Sn,且![]() N*).
N*).
(1)证明:数列{an+3}是等比数列;
(2)数列{an}中是否存在三项成等差数列?若存在,请求出一组;若不存在,请说明理由.
19. 
 (本大题满分12分)
(本大题满分12分)
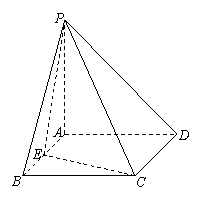
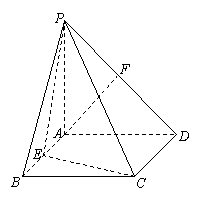
在直角梯形P1DCB中,P1D∥CB,CD⊥P1D,P1D=6,BC=3,DC=![]() ,A是P1D的中点,E是线段AB的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角.
,A是P1D的中点,E是线段AB的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角.
(1)求证:PA⊥平面ABCD;
(2)求平面PEC和平面PAD所成的二面角(锐角)的大小.
20.  (本大题满分12分)
(本大题满分12分)
某种商品在30天内的销售价格P(元)与时间t (天)的函数关系用右图的两条线段表示,该商品在30天内日销售量Q (件)与时间t (天)之间关系的部分数据如下表.
|

(1)写出该商品的销售价格P与时间t的函数关系式;
(2)根据表中提供的数据确定一个近似描述日销售量Q与时间t的函数关系式;
(3)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?(日销售金额=销售价格×日销售量).
21. (本大题满分12分)
设f (x)是定义在[-1,1]上的偶函数,g(x)的图象与f (x)的图象关于直线x=1对称,且当x∈[2,3]时,g(x)=2a(x-2)-4(x-2)3222233.
(1)求f (x)的解析式;
(2)是否存在正整数a,使f (x)的图象的最高点落在直线y=12上?若存在,求出a的值;若不存在,请说明理由.
22. (本大题满分14分)
已知△OPQ的面积为S,且![]() ,
,![]() ,
,![]() ,以O为中心,P为焦点的椭圆经过点Q.
,以O为中心,P为焦点的椭圆经过点Q.
(1)当m![]() (1,2]时,求
(1,2]时,求![]() 的最大值,并求出此时的椭圆C方程;
的最大值,并求出此时的椭圆C方程;
(2)在(1)的条件下,过点P的直线l与椭圆C相交于M、N两点,与椭圆C对应于焦点P的准线相交于D点,且![]() ,请找出
,请找出![]() 之间的关系,并证明你的结论.
之间的关系,并证明你的结论.
数学(理工农医类)参考答案及评分标准
命题人:郭仁俊
说明:
1.本解答指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
2.对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,选择题和填空题不给中间分数.
一.选择题:ACCA BDAC CAAA
二.填空题:13.11 14.(-∞,-3] 15.①②④ 16.14
三.解答题:
17.解:由已知![]() ,即
,即![]() , 2分
, 2分
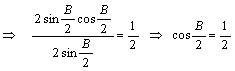 4分
4分
又0<B<![]() ,
,![]()
![]() ,即
,即![]() 6分
6分
![]()
![]() 8分
8分
![]() 0<A<
0<A<![]() ,
∴
,
∴![]()
![]()
![]() ,1],
,1], ![]()
![]() ,1] 12分
,1] 12分
18.解:(1)由已知,得![]() N*) ∴
N*) ∴![]()
两式相减得 ![]()
∴![]() 2分
2分
∴![]() (n
(n![]() N*)
N*)
又![]() ∴a1=3,a1+3=6
∴a1=3,a1+3=6
故数列![]() 是首项为6,公比为2的等比数列 4分
是首项为6,公比为2的等比数列 4分
(2)由(1)![]() ∴
∴![]() 6分
6分
假设![]() 中存在三项依次为
中存在三项依次为![]() (m1<m2<m3),它们可以构成等差数列,
(m1<m2<m3),它们可以构成等差数列,
则![]()
即![]() 8分
8分
上式两边同除以![]() ,得
,得![]() ① 10分
① 10分
∵m1、m2、m3![]() N*,且m1<m2<m3
N*,且m1<m2<m3
∴①式的左边是偶数,右边是奇数 ∴①式不能成立
∴数列![]() 中不存在构成等差数列的三项 12分
中不存在构成等差数列的三项 12分
 19.(1)证:
19.(1)证:![]() AB
AB![]() PA,AB
PA,AB![]() AD
AD
![]() AB
AB![]() 平面PAD
2分
平面PAD
2分
![]() AB∥DC,
AB∥DC,![]() DC
DC![]() 平面PAD
平面PAD
DC![]() PD DC
PD DC![]() AD
AD
![]() PDA为二面角P-CD-B的平面角 4分
PDA为二面角P-CD-B的平面角 4分
故![]() PDA=45°
PDA=45°
![]() PA=AD=3
PA=AD=3 ![]() PDA=45°,
PDA=45°,
![]() PA
PA![]() AD
AD
又PA![]() AB ,
AB ,![]() PA
PA![]() 平面ABCD 6分
平面ABCD 6分
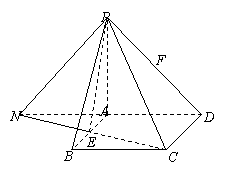 (2)解法一:以
(2)解法一:以![]() 为x轴、y轴、z轴建立直角坐标系,则
为x轴、y轴、z轴建立直角坐标系,则
B(![]() ,0,0),C(
,0,0),C(![]() ,3,0),D(0,3,0),P(0,0,3),
,3,0),D(0,3,0),P(0,0,3),
E(![]() ,0,0) 8分
,0,0) 8分
由(1)知![]() ,0,0)是平面PAD的法向量,设平面PEC的法向量为n=(1,y,z),则
,0,0)是平面PAD的法向量,设平面PEC的法向量为n=(1,y,z),则
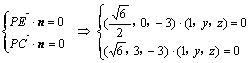 10分
10分
解得![]() ,∴n=(1,
,∴n=(1,![]() )
)
设向量![]() 与n所成的角为
与n所成的角为![]() ,则
,则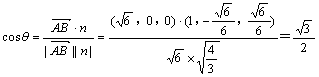
∴向量![]() 与n所成的角为30°,故平面PEC和平面PAD所成的二面角为30°. 12分
与n所成的角为30°,故平面PEC和平面PAD所成的二面角为30°. 12分
解法二:延长DA,CE交于点N,连结PN
![]() AE//CD 且E为AB中点
AE//CD 且E为AB中点
∴AE=![]() CD AE为△NDC的中位线
CD AE为△NDC的中位线
∴AN=AD=PA ![]() PND为Rt
PND为Rt![]() 8分
8分
又NE=EC=![]() PE=
PE=![]()
![]() PNC为Rt
PNC为Rt![]() ,∴PC
,∴PC![]() PN PD
PN PD![]() PN
PN
∴![]() CPD为平面PEC和平面PAD所成二面角的平面角 10分
CPD为平面PEC和平面PAD所成二面角的平面角 10分
又PD=![]() ,CD=
,CD=![]() ,PD
,PD![]() DC,tan
DC,tan![]() CPD=
CPD=![]()
∴![]() CPD=30°,即平面PEC和平面PAD所成二面角为30°. 12分
CPD=30°,即平面PEC和平面PAD所成二面角为30°. 12分
20.解:(1)根据图像,每件的销售价格P与时间t的函数关系式为:
![]() 3分
3分
(2)在直角坐标系中描出实数对(t,Q)的对应点,从图像发现点(5,35),(15,25),(20.20),(30.10)在同一条直线上,为此假设它们共线于直线l:Q=kt+b
由点(5,35)、(30,10)确定l的解析式为Q=-t+40,通过检验可知,点(15,25),(20,20)也在直线l上.
∴日销售量Q与时间t的一个函数关系式为Q=-t+40 (0<t≤3,t∈N= 6分
(3)设日销售金额为y(元),则
![]() 9分
9分
若0<t<25(t∈N),则当t=10时,ymax=900 10分
若25≤t≤30(t∈N),则当t=25时,ymax=1 125 11分
∴ymax=1 125。
∴这种商品日销售金额的最大值为1 125元,30天中的第25天的日销售金额最大. 12分
21.解:(1)当x∈[-1,0]时,2-x∈[2,3],f (x)=g(2-x)=-2ax+4x3
当x∈(0,1]时,f (x)=f(-x)=2ax+4x3,
∴![]() 4分
4分
(2) f (x)的图象的最高点落在直线y=12上,即函数的最大值为12
f (x)为偶函数,故只需研究函数f (x)=2ax-4x3在x∈(0,1]的最大值. 6分
令f / (x)=2a-12x2=0,得![]() 8分
8分
若![]() ∈(0,1],即0<a≤6,则
∈(0,1],即0<a≤6,则
![]() ≤12
≤12
故此时不存在符合题意的a; 10分
若![]() >1,即a>6,则f (x)在(0,1]上为增函数,于是
>1,即a>6,则f (x)在(0,1]上为增函数,于是![]() .
.
令2a-4=12,得a=8.
综上,存在a=8满足题设. 12分
22.解:(1)以O为原点,![]() 所在直线为x轴建立直角坐标系 2分
所在直线为x轴建立直角坐标系 2分
则P(m,0),设Q(x0,y0),由已知![]()
∴![]()
由![]() 得
得![]()
∴![]() ∴
∴![]() 4分
4分
令![]() ,则
,则![]()
当m∈(1,2]时,f / (m)>0,∴f (m)在(1,2]上是增函数,
∴当m=2时,![]() 的最大值为
的最大值为![]() 6分
6分
此时P(2,0),椭圆另一焦点为P / (-2,0),则椭圆长轴长![]()
∴![]() ,
,![]() ,故椭圆方程为
,故椭圆方程为![]() 8分
8分
(2)方法一:当直线l与x轴重合时,M(![]() ,0)、N(
,0)、N(![]() ,0)、D(5,0)
,0)、D(5,0)
这时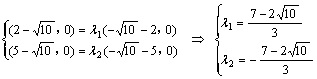
猜想:![]()
设过P(2,0)的直线方程,y=k(x-2)
由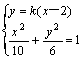 得:(3+5k2)x2-20k2x+20k2-30=0 10分
得:(3+5k2)x2-20k2x+20k2-30=0 10分
设l与椭圆的两交点为M(x1,y1)、N(x2,y2)
则![]() 11分
11分
由题意P、D分![]() 的比为
的比为![]()
∴
![]() 12分
12分
∴![]()
![]()
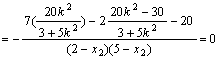
故![]() 14分
14分
|
|
方法二:由题意P、D分![]() 的比为
的比为![]()
过M、N分别作准线的垂线,垂足分别为M1、N1
由定比分点的意义及椭圆的定义得:
![]()
∴![]() 14分
14分