2005年江苏省启东中学高三数学
模拟试卷(二)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 若非空集合A={x![]() 2a+1≤x≤3a-5},B={x3≤x≤22},则能使AÍA
2a+1≤x≤3a-5},B={x3≤x≤22},则能使AÍA![]() B成立的所有a的集合是
( )
B成立的所有a的集合是
( )
A、{a1≤a≤9} B、{a6≤a≤9} C、{aa≤9} D、![]()
2.1!+2·2!+3·3!+…n·n!= ( )
A、(n+1)!-1 B、(n+1)! C、(n+1)!+1 D、(n+2)!
3.正三角形ABC中,![]() =
=![]() ,
,![]() ,
,![]() 边长为1,则
边长为1,则![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4.设函数![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5.已知:双曲线![]() ,其右支上的一点p,F1,F2为其两焦点,则△F1F2的内切圆在x轴上的切点Q的坐标
(
)
,其右支上的一点p,F1,F2为其两焦点,则△F1F2的内切圆在x轴上的切点Q的坐标
(
)
A、(b,0)
B、(a,0)
C、(![]() D、不确定
D、不确定
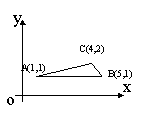
6. 给出平面区域如图,若使目标函数z=x+ay (a>0),取得最大值的最优解有无数个,则a的一个可能的取值为 ( )
(A)1 (B)3 (C)-1 (D)-3
7.在△ABC中,3sinA+4cosB=6,4sinB+3cosA=1,则∠C的大小 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8.棱锥P一ABCDEF的底面是正六边形,侧棱PA⊥面ABF,则下列命题中正确的有几个( )
①∠PDA是侧面PDC与底面所成的二面角的平面角 ②PC的长就是点P到直线CD的距离
③∠PCB是侧棱PC与底面所成的角 ④EF的长是点E到平面AFP的距离
A、 1 B、 2 C、 3 D、 4
9.一个单位有1000名职工,其中不到35岁的人有250人,35到49岁的人有560人,50岁以上的有190人,要从中抽取一个容量为200的样本,较为恰当的抽样方法有是( )
A、简单随机抽样 B、分层抽样 C、系统抽样 D、以上方法均可
10.直线![]() 绕原点按顺时针方向旋转30°后,所得的直线与圆
绕原点按顺时针方向旋转30°后,所得的直线与圆![]() 的位置关系是
( )
的位置关系是
( )
A、直线过圆心 B、直线与圆相切
C、直线与圆相离 D、直线与圆相交但不过圆心
11.已知![]() (
)
(
)
A、至少有一实数根 B、至少有一实根 C、无实根 D、有唯一实数根
12.由等式![]()
![]() 定义映射
定义映射![]() ( )
( )
A、(1,2,3,4) B、(0,3,4,0) C、(-1,0,2,-2) D、(0,-3,4,-1)
第Ⅱ卷(满分90分)
二、填空题:本大题共4小题,每小题4分,共16分.答案填在题中横线上.
13.如果直线沿向量![]() 则直线l的斜率是__________.
则直线l的斜率是__________.
14.某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个),经过3小时,这种细菌由1个可繁殖成_________ .
15.椭圆![]() 长轴上一个顶点为A,以A为直角顶点作一个内接于椭圆的等腰三角形,该三角形的面积是___________.
长轴上一个顶点为A,以A为直角顶点作一个内接于椭圆的等腰三角形,该三角形的面积是___________.
16.设函数![]() 请写出一个满足条件的函数
.此函数的单调性是
.
请写出一个满足条件的函数
.此函数的单调性是
.
三.解答题:(本大共6小题,17---21题每小题12分,第22题14分,共74分。)
17.甲乙两名篮球运动员,投篮命中率分别是0.9与0.8。
(1)如果每人投篮一次,求甲、乙两人至少有一人进球的概率。
(2)如果每人投篮3次,求甲投进2球且乙投进一球的概率。(结果保留两个有效数字)
18.已知函数![]() 。
。
1)当a=1时,救f(x)的单调递增区间;
2)当a<0时,且x∈[0,π]时,f (x)的值域是[3,4],求a,b的值。
19、(本小题满分12分)正四面体A-BCD的棱长为1,
(Ⅰ)如图(1)M为CD中点,求异面直线AM与BC所成的角;
(Ⅱ)将正四面体沿AB、BD、DC、BC剪开,作为正四棱锥的侧面如图(2),求二面角M-AB-E的大小;
(Ⅲ)若将图(1)与图(2)面ACD重合,问该几何体是几面体
(不需要证明),并求这几何体的体积。
 |  | ||
20、(本小题满分12分)已知函数![]()
(Ⅰ)是否存在实数使函数![]() 在R上是单调函数?
在R上是单调函数?
(Ⅱ)若x∈[0,1],函数![]() 上任意一点切线的斜率为k,讨论|k|≤1的充要条件.
上任意一点切线的斜率为k,讨论|k|≤1的充要条件.
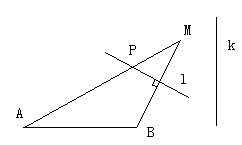
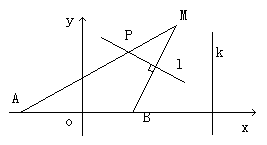 21. (本小题满分12分) 已知如图, A,B为两个定当,且
21. (本小题满分12分) 已知如图, A,B为两个定当,且![]() =2,动点M到A点的距离是4,线段MB的垂直平分线
=2,动点M到A点的距离是4,线段MB的垂直平分线![]() 交MA与点P,直线k
交MA与点P,直线k![]() AB,且点B到直线k的距离为3。
AB,且点B到直线k的距离为3。
(1) 求证:点P到点B的距离与到直线K的距离的比为定值。
(2) 若点P到A,B两点的距离之积为m,当m取最大值时,求P点的坐标
(3)
若![]()
![]() .
.
22.(本小题满分14分)
已知等比数列{a n}的首项为![]() ,公比是
,公比是![]() 展开式中第二项.
展开式中第二项.
(1)用n和x表示数列{a n}的通项a n;
(2)若数列{an}的前n项和为Sn,用n和x表示![]() ;
;
(3)若g(x)=(x-1)![]() ,其导数为g/(x),且0<x<1,求证:
,其导数为g/(x),且0<x<1,求证:![]() <2n[
<2n[![]() .
.
参考解答
1.B 2.A 3.A 4.B 5.B 6.A 7.C 8.A 9.B 10.B 11.D 12.D
13. ![]() 14. 512 15.
14. 512 15. ![]() 16.
16. ![]() ,增函数
,增函数
三.解答题:
17解:设甲乙两人投篮的事件分别为A、B,则p(A)=0.9,p(B)=0.8
1) p(A∪B)=p(A∩![]() )+ p(
)+ p(![]() ∩B) + p(A∩B)=0.98
∩B) + p(A∩B)=0.98
或p(A∪B)=1-p(![]() ∩
∩![]() )=0.98
)=0.98
2) p=C32[p(A)]2[1-p(A)]1 C31[p(B)]1[1-p(B)]2=0.023
18.解:(1) ∵a=1, ∴![]() +sinx+b=sinx+cosx+b+1=
+sinx+b=sinx+cosx+b+1=![]() ,∵y=sinx的的单调增区间为[2kπ
,∵y=sinx的的单调增区间为[2kπ![]() ,2kπ
,2kπ![]() ] (k∈Z),
] (k∈Z),
∴当2kπ![]() ≤x+
≤x+![]() ≤2kπ
≤2kπ![]() 即2kπ-
即2kπ-![]() ≤x≤2kπ+
≤x≤2kπ+![]() (k∈Z)时,f (x)是增函数,所以f (x)的单调增区间是[2kπ-
(k∈Z)时,f (x)是增函数,所以f (x)的单调增区间是[2kπ-![]() ,2kπ+
,2kπ+![]() ] (k∈Z)
] (k∈Z)
(2):由(1)得f (x)=![]() +a+b,∵x∈[0,π],∴
+a+b,∵x∈[0,π],∴![]() ≤x+
≤x+![]() ≤
≤![]()
∴![]() ≤sin( x+
≤sin( x+![]() )≤1,又∵a<0,
)≤1,又∵a<0,![]() a≤
a≤![]() ≤-a,
≤-a,
∴![]() a +a+b≤f
(x)≤b,∵f (x)的值域是[3,4],∴
a +a+b≤f
(x)≤b,∵f (x)的值域是[3,4],∴![]() a +a+b=3且b=4
a +a+b=3且b=4
解得a= 1-![]() ,b=4。
,b=4。
19. 【解】(Ⅰ)取BD的中点,连结AN、MN,

![]() MNAB
MNAB
![]()
![]() AMN就是异面直线AM与BC所成的角,………2分
AMN就是异面直线AM与BC所成的角,………2分
在![]() AMN中,AM=AN=
AMN中,AM=AN=![]() ,MN=
,MN=![]() ,
,
![]()
![]() AMN=arccos
AMN=arccos![]() .…………………4分
.…………………4分
(Ⅱ)取BE中点P,连结AP、PM,作MQ![]() AP于Q,
AP于Q,
过Q作QH![]() AB于H,连MH;
AB于H,连MH;

![]() EB
EB![]() AP,EB
AP,EB![]() PM,
PM,
![]() EB
EB![]() 面APM,即EB
面APM,即EB![]() MQ,
MQ,
![]() MQ
MQ![]() 面AEB
面AEB
![]() HQ为MH在面AEB上的射影,即MH
HQ为MH在面AEB上的射影,即MH![]() AB
AB
![]()
![]() MHQ就是M-AB-E的平面角,…………………6分
MHQ就是M-AB-E的平面角,…………………6分
在![]() AMP中,AM=AP=
AMP中,AM=AP=![]() ,PM=1,MQ=
,PM=1,MQ=![]() ,PQ=
,PQ=![]() ;
;
在![]() ABP中,
ABP中,![]() AHQ=300,AQ=AP-PQ=
AHQ=300,AQ=AP-PQ=![]() -
-![]() ,AQ=
,AQ=![]() ,HQ=
,HQ=![]() ;
;

![]()
![]() MHQ=arctan4
MHQ=arctan4![]() ,…………………8分
,…………………8分
(Ⅲ)若将图(1)与图(2)面ACD重合,
该几何体是5面体…………………10分
这斜三棱柱的体积=3VA-BCD
=3´![]() ´
´![]() ´
´![]() =
=![]() …………………12分
…………………12分
20.【解】(Ⅰ) ∵![]() ∴
∴![]() ∴
∴![]() 不可能恒大于0,
不可能恒大于0,
若![]() 恒成立,则a=0,故当a=0,b∈R时函数
恒成立,则a=0,故当a=0,b∈R时函数![]() 在R上是单调减函数. (4分)
在R上是单调减函数. (4分)
(Ⅱ)当 x∈[0,1]时, ![]() ,由题意得:
,由题意得:![]() , x∈[0,1]
, x∈[0,1]
即对任意x∈[0,1],![]() 等价于
等价于![]() ,
,![]() ,
,![]() ,的值满足:
,的值满足:
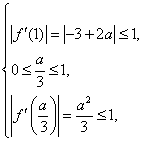 或
或 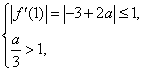 或
或 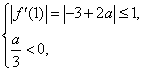
即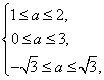 或
或![]() 或
或![]()
所以 ![]() 即|k|≤1的充要条件是
即|k|≤1的充要条件是![]() (12分)
(12分)
21.【解】以直线AB为x轴,线段AB的中垂线为y轴,建立直角坐标系,则A(-1,0),B(1,0),直线k:x=4.
(1)![]()
![]() 是MB中垂线,
是MB中垂线,![]() ,
,![]() 点P的轨迹是以A,B为焦点,长轴长为4的椭圆,其右准线为k:
点P的轨迹是以A,B为焦点,长轴长为4的椭圆,其右准线为k:![]() ,且其离心率为
,且其离心率为![]() =
=
![]() ,故P到B的距离与到直线k距离之比为定值
,故P到B的距离与到直线k距离之比为定值![]() 。
。
(2) ![]()
![]()
![]() m=PAPB≤
m=PAPB≤![]() =4。当且仅当PA=PB时取等号。此时m的最大值 为4,P为椭圆短轴的两个端点,坐标为P(0,
=4。当且仅当PA=PB时取等号。此时m的最大值 为4,P为椭圆短轴的两个端点,坐标为P(0,![]() )或P(0,-
)或P(0,-![]() )
)
(3)由![]() 解得PA=5/2,PB=3/2,又AB=2在△PAB中,
解得PA=5/2,PB=3/2,又AB=2在△PAB中,
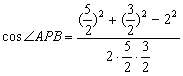 =
=![]() 。
。![]() =
=![]() .
.
22. 【解】(1)由![]() ,解得
,解得![]() ,∴m=3,a1=
,∴m=3,a1=![]() =1,而
=1,而![]() 展开式第二项为
展开式第二项为![]() =x,∴a1=xn-1;
=x,∴a1=xn-1;
(2) 当x=1时,Sn=n,∴![]() =
=![]() =
=![]() =n·2n-1;
=n·2n-1;
当x≠1时,Sn=![]() ,
,![]() =
=![]()
=![]() (
(![]() -
-![]() )=
)=![]() [
[![]() ]
]
∴![]() =
=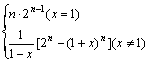
(3)当0<x<1时,g(x)=(x-1)![]() =
=![]() -
-![]() ,
,
![]() =
=![]()
∴![]() =
=![]() =1+
=1+![]() ①
①
![]()
![]() =
=![]() =1
=1![]()
![]() +
+![]() ②
②
由①-②得,![]() =
=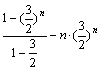 ,
,
∴![]() =
=![]() ,∴
,∴![]() -2n[
-2n[![]() =4+
=4+![]() ,
,
∵![]() ]
]
=4+2n+[![]() ]>2n+4,
]>2n+4,
∴![]() <2n[
<2n[![]()