2005年江苏省如皋中学高三质量调研卷数学试题(二)
姓名__________学号__________班级___________
一选择题
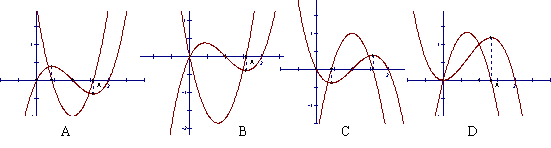 1.以下四图,都是同一坐标系中三次函数及其导函数的图象,其中一定不正确的序号是
1.以下四图,都是同一坐标系中三次函数及其导函数的图象,其中一定不正确的序号是
2.以平行六面体相邻两个面上互相异面的两条面对角线的端点为顶点的四面体的体积是平行六面体体积的:
A. B. C. D.
3.设M={平面内的点(a,b)},N={f(x)f(x)=acos2x+bsin2x} ,给出M到N的映射:
f:(a,b)![]() f(x)= acos2x+bsin2x。则点(1,)的象f(x)的最小正周期为:
f(x)= acos2x+bsin2x。则点(1,)的象f(x)的最小正周期为:
A.π B.2π C. D.
4.等差数列![]() 的前n项和记为
的前n项和记为![]() ,若
,若![]() 为一个确定的常数,则下列各数中也是常数的是
为一个确定的常数,则下列各数中也是常数的是
A.![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
5.编辑一个运算程序:1&1 = 2 , m&n = k , m&(n + 1) = k + 2,则 1&2005 的输出结果为 ( )
A 4008 B 4006 C 4012 D 4010
6.给定下列命题:
(1)y=sinx在第一象限是增函数
(2)△ABC中三内角A、B、C成等差的充要条件是B=60°
(3)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC是正三角形
(4)函数y=Asin(ωx+φ)的周期是T=![]() ,其中正确命题的序号为 ( )
,其中正确命题的序号为 ( )
A.①②③④ B.①④ C.②③ D.①②④
7.不等式![]() 对任意
对任意![]() 都成立,则
都成立,则![]() 的取值范围为
( B
)
的取值范围为
( B
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8. 已知函数![]() 在
在![]() 处有极值10,则
处有极值10,则![]() 等于
等于
(A) 11或18 (B) 11 (C) 18 (D) 17或18
9.若![]() 展开式中第32项与第72项的系数相同,那么展开式的中间一项的系数为
展开式中第32项与第72项的系数相同,那么展开式的中间一项的系数为
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
10.设![]() 为偶函数,对于任意的
为偶函数,对于任意的![]() 的数,都有
的数,都有![]() ,已知
,已知![]() ,那么
,那么![]() 等于
等于
(A) 2
(B) ![]() (C) 8 (D)
(C) 8 (D) ![]()
二填空题
11.已知集合![]() ,集合
,集合![]() ,则集合
,则集合![]()
![]() ______________ 。
______________ 。
12.已知函数![]() ,若对任意
,若对任意![]() 有
有![]() 成立,则方程
成立,则方程![]() 在
在![]() 上的解为 _____________ 。
上的解为 _____________ 。
13.数列![]() 的首项为
的首项为![]() ,且
,且![]() ,记
,记![]() 为数列
为数列![]() 前
前![]() 项和,则
项和,则![]()
![]() __________________。
__________________。
14.已知向量![]() ,其夹角为
,其夹角为![]() ,则直线
,则直线![]() =0与圆
=0与圆![]() 的位置关系是_________.
的位置关系是_________.
15.将最小正周期为![]() 的函数
的函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到偶函数图象,则满足题意的
个单位,得到偶函数图象,则满足题意的![]() 的一个可能值为 __________ 。
的一个可能值为 __________ 。
16.若函数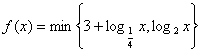 ,其中
,其中![]() 表示
表示![]() 两者中的较小者,
两者中的较小者,
则![]() 的解为 _____________ 。
的解为 _____________ 。
三解答题
17.已知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() (
(![]() 为常数)。
为常数)。
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,求
时,求![]() 在
在![]() 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的![]() ,并猜想
,并猜想![]() 在
在![]() 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);
(3)当![]() 时,证明:函数
时,证明:函数![]() 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线![]() 上。
上。
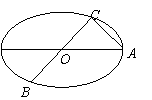 18.如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
18.如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且![]() ,BC=2AC.
,BC=2AC.
(1)建立适当的坐标系,求椭圆方程;
(2)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,证明:![]() .
.
答案:1. B 2. B 3. A 4. B 5. A 6. B 7. C 8. B 9. D 10. D
11.![]() 12.
12.![]() 13.
13.![]() 14. 相交 15.
14. 相交 15. ![]()
16.![]()
17.解![]() 时,
时,![]() , 则
, 则 ![]()
∵函数![]() 是定义在
是定义在![]() 上的奇函数,即
上的奇函数,即![]()
∴![]() ,即
,即 ![]() ,又可知
,又可知 ![]()
∴函数![]() 的解析式为
的解析式为 ![]() ,
,![]()
(2)![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]()
∵ 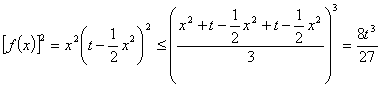
∴![]() ,即
,即 ![]()
![]() 时,
时,![]() 。
。
猜想![]() 在
在![]() 上的单调递增区间为
上的单调递增区间为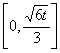 。
。
(3)![]() 时,任取
时,任取![]() ,∵
,∵![]()
∴![]() 在
在![]() 上单调递增,即
上单调递增,即![]() ,即
,即![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()
∴当![]() 时,函数
时,函数![]() 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线![]() 上
上
.18. (1)解:以O为原点,OA为x轴建立直角坐标系,设A(2,0),
则椭圆方程为![]() --------------------------- 2分
--------------------------- 2分
∵O为椭圆中心, ∴由对称性知OC=OB
又∵![]() , ∴AC⊥BC
, ∴AC⊥BC
又∵BC=2AC, ∴OC=AC
∴△AOC为等腰直角三角形
∴点C的坐标为(1,1) ∴点B的坐标为(-1,-1) --------------------------------- 4分
将C的坐标(1,1)代入椭圆方程得![]() ,
,
则求得椭圆方程为![]() ------------------------------------------------------------- 6分
------------------------------------------------------------- 6分
(2)证:由于∠PCQ的平分线垂直于OA(即垂直于x轴),
不妨设直线PC的斜率为k,则直线QC的斜率为-k,
因此直线PC、QC的方程分别为y=k(x-1)+1,y=-k(x-1)+1
由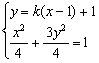 得:
得:
(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 (*)--------------------------------------------8分
∵点C(1,1)在椭圆上, ∴x=1是方程(*)的一个根,
∴xP•1=![]() 即
xP=
即
xP=![]()
同理xQ=![]() -------------------------------------------------------------------- 10分
-------------------------------------------------------------------- 10分
∴直线PQ的斜率为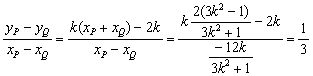 ---------12分
---------12分
又∵![]() ,∴
,∴![]() .---------------------------------------------------13分
.---------------------------------------------------13分