南通市高三第二次调研考试1

2005年南通市高三第二次调研数学考试

一、选择题：本大题共10小题，每小题5分，共50分．

1．  命题“若，则”的逆否命题是

A.若，则　　　　　  B.若，则

C.若a ≤b，则　　　　　  D.若，则a ≤b

2．  椭圆的右焦点到直线的距离是

A.　　　　　　  B.　　　　　 C.1　　　　　　 D.

3．  在等比数列{a_n}中，则等于

A.或　　  B.　　　　C.　　　 D. 或

4．  将函数的图象按向量a平移后得到函数的图象，则向量a可以是

A.　　　　　 B. 　　　　　C. 　　　　D.

5．  如图，长方体ABCD-A₁B₁C₁D₁中，∠DAD₁＝45°，∠CDC₁＝30°，

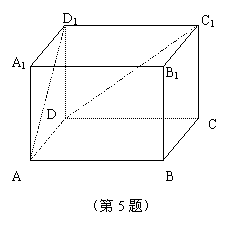那么异面直线AD₁与DC₁所成角的大小是

　 A.　　　　　　　 B.

　 C. 　　　　　　 D.

6．  的值为

A.1022　 B.1023　 C.2046　　D.2047

7．  已知且，则的取值范围是

A.　　B.

　 C. 　　 D.

8．  定义在R上的函数f（x）对任意的实数x满足f (x+1)＝－f (x－1)，则下列结论一定成立的是

A. f (x)是以4为周期的周期函数　　  B. f (x)是以6为周期的周期函数

　 C. f (x)的图象关于直线x＝1对称　　 D. f (x)的图象关于点（1,0）对称

9．  甲、乙两人玩猜骰子游戏．游戏的规则是：有三个骰子（每个骰子都是正方体，其六个面上分别标有数字1,2,3,4,5,6），乙先从1,2,3,4,5,6这六个数中报一个，然后由甲掷这三个骰子各一次，如果三个骰子中至少有1个骰子的向上一面的数字恰好是乙报的这个数，那么乙获胜，否则甲获胜．若骰子任意一面向上的概率均等，则乙获胜的概率是

　　 A.　　　　B. 　　　　　C. 　　　　　D.

10．已知平面上点P∈，则满足条件的点P在平面上所组成图形的面积是

A.36π　　　 　B.32π　　　　 C.16π　　　 　D.4π

二、填空题：本大题共4小题；每小题4分，共16分．

11．函数的最小值是　　　　　　　　　　　　　  ．

12．已知椭圆与双曲线具有相同的焦点F₁，F₂，设两曲线的一个交点为Q,∠QF₁F₂＝90°，则双曲线的离心率为　　　　　　　　　　　　　　　　 ．

13．函数在区间（1，+∞）上是单调增函数，则a的取值范围是　　　　  ．

14．设函数的定义域为R.若存在与x无关的正常数M，使≤对一切实数x均成立，则称为有界泛函．在函数

中，属于有界泛函的有　　　　　　　　  .

三、解答题：本大题共6小题；共84分，

15．（本小题满分14分）

已知S_n是等比数列{a_n}的前n项和，成等差数列.

(1)　　求数列{a_n}的公比q；

(2)　　试问的等差中项是数列{a_n}中的第几项？请说明理由.

16．（本小题满分14分）

已知向量a=(1,2),b=(－2,1),k ,t为正实数，向量x=a+(t²+1)b, y=－ka+b.

（1）　　　 若x⊥y，求k的最小值；

（2）　　　 是否存在k , t ,使x∥y？若存在，求出k的取值范围；若不存在，请说明理由.

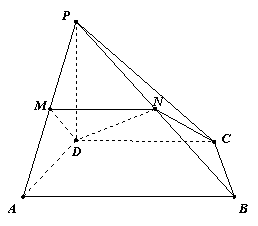17. （本小题满分15分）

　　 在四棱锥P－ABCD中，AD⊥AB，CD∥AB，PD⊥底面ABCD，,直线PA与底面ABCD成60°角，点M、N分别是PA、PB的中点．

（1）　　　 求二面角P－MN－D的大小；

（2）　　　 如果△CDN为直角三角形，求的值．

18．（本小题满分13分）

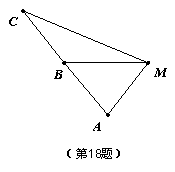
如图，已知A、B、C是一条直路上的三点，AB与BC各等于1km，从三点分别遥望塔M，在A处看见塔在北偏东45°方向，在B处看见塔在正东方向，在点C处看见塔在南偏东60°方向，求塔到直路ABC的最短距离．

19．（本小题满分15分）

设定义在R上的函数（其中∈R，i=0,1,2,3,4），当x= －1时，f (x)取得极大值，并且函数y=f (x+1)的图象关于点（－1，0）对称．

（1）　　　 求f (x)的表达式；

（2）　　　 试在函数f (x)的图象上求两点，使这两点为切点的切线互相垂直，且切点的横坐标都在区间上；

（3）　　　 若，求证：

20．（本小题满分13分）

设M是椭圆上的一点，P、Q、T分别为M关于y轴、原点、x轴的对称点，N为椭圆C上异于M的另一点，且MN⊥MQ，QN与PT的交点为E，当M沿椭圆C运动时，求动点E的轨迹方程．

参考答案

1.D　　2.A　　3.D　　4.B　　5.C　　6.C　　7.A　　8.A　　9.B　　10.B

11．－5　　12.　　13.　　14.

15．解：（1）不适合, 时,解得

（2）的等差中项是数列{a_n}中的第10项.

16．解：（1）,由基本不等式求得k的最小值为2　　　

（2）假设存在正实数k，t，使得x∥y，则

　　　　整理，得 正实数k，t不存在。

17．解法一：（1）∠PMD为二面角P－MN－D的平面角。…………4分

　　　　　　　  计算得二面角P－MN－D的大小为120°。…………8分

　　　　　 （2）①若∠CDN＝90°，与题意不符………………10分

②若∠DCN＝90°，可算得…………12分

③若∠DNC＝90°，可算得…………15分

　　　　解法二：用向量方法(略)

18．解法一：得,由余弦定理得

　　　　　  由面积关系得

　　　　 　 求得

　　　 解法二：以点B为坐标原点，BM直线为x轴建立平面直角坐标系，

　　　　　　　 设M（a,0）,A(b,c),则C（－b,－c）………………2分

可得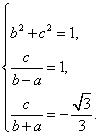,解得又故直线AB的方程为设点M到直线AB的距离为，则，所以答：略.

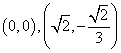19．解：（1）　（2）或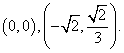

 （3）用导数求最值，可证得……

20．解：设点的坐标

则

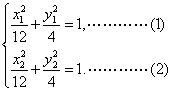　　　　 由（1）－（2）可得

　　　又MN⊥MQ，所以

　　　直线QN的方程为，又直线PT的方程为

　　　从而得所以

　　　代入（1）可得此即为所求的轨迹方程.