高三数学同步检测(十二)
第三章单元检测(B)
说明:本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案填入题后括号内，第Ⅱ卷可在各题后直接作答.共100分，考试时间90分钟.
第Ⅰ卷(选择题共40分)
一、选择题(本大题共10小题，每小题4分，共40分)
1.已知y=
sin2x+sinx+3,那么y′是（ ）
A.仅有最小值的奇函数
B.既有最大值又有最小值的偶函数
C.仅有最大值的偶函数
D.非奇非偶函数
分析 本题主要考查导函数的性质.
解 y′=(sin2x)′+(sinx)′=(cos2x)(2x)′+cosx=cos2x+cosx.
不妨设f(x)=cos2x+cosx，
∵f(-x)=cos(-2x)+cos(-x)=cos2x+cosx=f(x),∴y′为偶函数.
又由于y′=2cos2x-1+cosx=2cos2x+cosx-1,
令t=cosx(-1≤t≤1),
∴y′=2t2+t-1=2(t+
)2-
.
∴y′max=2,y′min=-.故选B.
答案 B
2.函数y=ax3-x在（-∞,+∞)上是减函数，则（ ）
A.a=
B.a=1
C.a=2
D.a<0
分析 本题考查常见函数的导数及其应用.可以采用解选择题的常用方法——验证法.
解 由y′=3ax2-1,当a=时，y′=x2-1,如果x>1,则y′>0与条件不符.同样可判断a=1,a=2时也不符合题意.当a<0时，y′=3ax2-1恒小于0，则原函数在（-∞,+∞)上是减函数.故选D
答案 D
3.已知f(x)=x3的切线的斜率等于1,则这样的切线有( )
A.1条 B.2条
C.多于2条 D.不能确定
分析 本题主要考查导数的几何意义的应用.切线的条数是由切点的个数确定的.
解 f′(x)=3x2,由f′(x)=3x2=1,
得x=±
.
所以符合条件的切线有2条.
答案 B
4.已知曲线y1=x2,y2=x3,y3=2sinx,这三条曲线与x=1的交点分别为A、B、C,又设k1、k2、k3分别为经过A、B、C且分别与这三条曲线相切的直线的斜率,则( )
A.k1<k2<k3 B.k3<k2<k1
C.k1<k3<k2 D.k3<k1<k2
分析 本题主要考查导数的几何意义及导数的运算法则.
解 ∵y1′=2x,y2′=3x2,y3′=2cosx,
∴y1′x=1=2,y2′x=1=3,y3′x=1=2cos1.
∴k3<k1<k2.
答案 D
5.★曲线y=x2+1在点(1,2)处的切线与x轴、直线x=3所围成的三角形的面积为( )
A.13 B.14 C.9 D.10
分析 本题考查导数的相关知识及三角形的面积公式.
解 ∵y=x2+1,∴y′=2x.
∴y′x=1=2,切线的方程为y-2=2(x-1),与x轴的交点(0,0)所围成的三角形的面积S=(3-0)×6=9.
答案 C
6.★设f0(x)=cosx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2006(x)等于( )
A.sinx B.cosx C.-sinx D.-cosx
分析 本题考查导数的运算及函数的周期性.
解 f1(x)=(cosx)′=-sinx,
f2(x)=(-sinx)′=-cosx,
f3(x)=(-cosx)′=sinx,
f4(x)=(sinx)′=cosx,
f4(x)=f0(x),f5(x)=f1(x),…,
fn+4(x)=f(x),可知该函数的周期为4.
∴f2006(x)=f2(x)=-cosx.
答案 D
7.★已知函数f(x)=x3+mx2+(m+6)x+1既存在极大值又存在极小值,则实数m的取值范围是( )
A.(-1,2) B.(-∞,-3)∪(6,+∞)
C.(-3,6) D.(-∞,-1)∪(2,+∞)
分析 本题考查导数与极值的关系.
解 f′(x)=3x2+2mx+(m+6).
∵函数f(x)既存在极大值又存在极小值,
∴函数f′(x)=3x2+2mx+(m+6)的图象与x轴相交,即4m2-4×3×(m+6)>0.
解得m<-3或m>6.
∴实数m的取值范围是(-∞,-3)∪(6,+∞).
答案 B
8.若函数f(x)的定义域为(0,+∞),且f(x)>0,f′(x)>0,那么函数y=xf(x)( )
A.存在极大值 B.存在极小值
C.是增函数 D.是减函数
分析 本题考查导数的应用.
解 ∵y=xf(x),∴y′=(x)′f(x)+xf′(x)=f(x)+xf′(x).又∵x>0,f(x)>0,f′(x)>0,
∴y′=f(x)+xf′(x)>0,
即函数y=xf(x)在(0,+∞)上是增函数.
答案 C
9.点P是曲线y=x2-lnx上任意一点,则点P到直线y=x-2的最小距离为( )
A.1 B.
C.
D.3
分析 本题考查导数的几何意义及点到直线的距离公式.
解 ∵y=x2-lnx,
∴y′=2x-
.
令2x-=1,得x=1或x=-(舍去).
当x=1时,y=x2-lnx=1.
此时点P(1,1)是到直线x-y-2=0距离最小的点.
∴d=
答案 B
10.已知抛物线y2=2px(p>0)与一个定点M(p,p),则抛物线上与M点的距离最小的点为（ ）
A.(0,0)
B.(
,p)
C.(
,p)
D.(
,
p)
分析 本题考查利用函数的导数求解函数的最值.首先建立关于距离的目标函数关系式,然后合理地选取变量,通过求导数的方法求与最值有关的问题.本题也可以用解析几何中数形结合法求解.
解 设抛物线上的任意点(x,y)到点M的距离为d,
则有d2=(p-x)2+(p-y)2=(p-
)2+(p-y)2.所以(d2)′=2(p-)(-
)+2(p-y)(-1)=
-2p.
令(d2)′y=0,即
-2p=0,解得y=
.这是函数在定义域内的唯一极值点,所以必是最值点.
代入抛物线方程得x==
=.
所以点(,p)为所求的点.
答案 D
第Ⅱ卷(非选择题共60分)
二、填空题(本大题共4小题，每小题4分，共16分.把答案填在题中横线上)
11.★曲线y=x3+3x2+6x-10的切线中,斜率最小的切线方程是 .
分析 本题考查常见函数的导数及导数的几何意义.
解 ∵y=x3+3x2+6x-10,
∴y′=3x2+6x+6=3(x+1)2+3.
∴(y′)min=3.
此时,x=-1,y=(-1)3+3×(-1)2+6×(-1)-10=-14.
∴斜率最小的切线方程是y+14=3(x+1),
即3x-y-11=0.
答案 3x-y-11=0
12.函数y=sin2x的单调递减区间是 .
分析 本题考查导数在三角问题上的应用
解法一 y′=2sinxcosx=sin2x.
令y′<0,即sin2x<0，
∴2kπ-π<2x<2kπ,k∈Z.
∴kπ-
<x<kπ,k∈Z.
∴函数y=sin2x的单调递减区间是(kπ-,kπ),k∈Z.
解法二 y=sin2x=-cos2x+,函数的减区间即cos2x的增区间，由2kπ-π<2x<2kπ,k∈Z,得kπ-<x<kπ,k∈Z.
∴函数y=sin2x的单调递减区间是（kπ-,kπ),k∈Z.
答案 (kπ-,kπ),k∈Z
13.点P在曲线y=x3-x+
上移动,设过点P的切线的倾斜角为α,则α的取值范围是 .
分析 本题主要考查导数的几何意义,以及直线的倾斜角与斜率之间的关系.
解 ∵y′=3x2-1,即tanα=3x2-1,
∴tanα∈［-1,+∞).
∴α∈［0,)∪［
,π).
答案 α∈［0,)∪［,π)
14.★若函数f(x)=loga(x3-ax)(0<a<1)在区间(-,0)内单调递增,则a的取值范围是 .
分析 本题考查复合函数的导数及单调性.
解 令u=x3-ax,u′=3x2-a.
∵0<a<1,若f(x)在(-,0)内单调递增,必须u′<0,即3x2-a<0在(-,0)内恒成立,a>3x2,∴a≥
.综上, ≤a<1.
答案 ≤a<1
三、解答题(本大题共5小题，共44分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分8分)氡气是一种由地表自然散发的无味的放射性气体.如果最初有500克氡气,那么t天后,氡气的剩余量为A(t)=500×0.834t.
(1)氡气的散发速度是多少?
(2)A′(7)的值是什么(精确到0.1)?它表示什么意义?
分析 本题考查常见函数的导数及导数的几何意义.
解 (1)氡气的散发速度就是剩留量函数的导数.
∵A(t)=500×0.834t,
∴A′(t)=500×0.834tln 0.834. 4分
(2)A′(7)=500×0.8347ln 0.834≈-25.5.
它表示在第7天附近,氡气大约以25.5克/天的速度自然散发. 8分
16.(本小题满分8分)某工厂需要建一个面积为512 m2的矩形堆料场，一边可以利用原有的墙壁，问堆料场的长和宽各为多少时，才能使砌墙所用的材料最省？
分析 本题考查如何求函数的最值问题，其关键是建立目标函数.
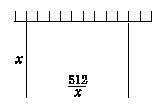解 要求材料最省就是要求新砌的墙壁总长度最短.如右图所示，设场地一边长为x m，则另一边长为
m，因此新墙总长度L=2x+(x>0),
2分
L′=2-
.
令L′=2-=0,得x=16或x=-16. 4分
∵x>0,∴x=16. 5分
∵L在(0,+∞)上只有一个极值点,
∴它必是最小值点.
∵x=16,∴=32.
7分
故当堆料场的宽为16 m，长为32 m时，可使砌墙所用的材料最省.8分
[注] 本题也可利用均值不等式求解.
17.★(本小题满分8分)某工厂生产某种产品,已知该产品的月生产量x(t)与每吨产品的价格p(元/t)之间的关系式为p=24 200-
,且生产x t的成本为R=50
000+200x(元).问该产品每月生产多少吨才能使利润达到最大?最大利润是多少?(利润=收入-成本)
分析 本题主要考查利用导数求函数的最值.根据题意,列出函数关系式,求导求解.
解 每月生产x吨时的利润为f(x)=(24
200-)x-(50 000+200x)=-
+24 000x-50 000(x≥0).
4分
由f′(x)=-
x2+24
000=0,
解得x1=200,x2=-200(舍去). 6分
∵f(x)在［0,+∞)内只有一个点x1=200使f′(x)=0,
∴它就是最大值点,f(x)的最大值为f(200)=3 150 000(元).
∴每月生产200 t才能使利润达到最大,最大利润是315万元. 8分
18.(本小题满分10分)已知曲线C1：y=x2与C2:y=-(x-2)2,若直线l与C1、C2都相切,求l的方程.
分析 本题主要考查导数几何意义的应用.要求具有某种性质的切线,只需求出对应的x0即可,一般要求出x0所需满足的方程或方程组,解之即可.
解 设直线l与C1相切于点(x1,x12),
∵y=x2,∴y′=2x.
∴
=2x1. 2分
∴l：y-x12=2x1(x-x1),即y=2x1x-x12. 3分
设直线l与C2相切于点(x2,-(x2-2)2),
∵y=-(x-2)2,
∴y′=-2(x-2).
∴
=-2(x2-2).
5分
∴l：y+(x2-2)2=-2(x2-2)(x-x2),
即y=-2(x2-2)x+x22-4. 6分
比较l的两个方程,应有
将x1=2-x2代入第二个方程,得-(2-x2)2=x22-4,
解得x2=0或x2=2,于是x1=2或x1=0. 8分
当x1=2,x2=0时,直线l经过两点(2,4)、(0,-4),
∴直线l的方程为y=4x-4;
当x1=0,x2=2时,直线l经过(0,0)、(2,0)两点.
∴直线l的方程为y=0. 10分
19.(本小题满分10分)已知A、B两地的距离是130 km.按交通法规规定,A、B两地之间的公路车速应限制在50~100
km/h.假设汽油的价格是4元/升,以x km/h速度行驶时,汽车的耗油率为(3+
) L/h,司机每小时的工资是14元.那么最经济的车速是多少?如果不考虑其他费用,这次行车的总费用在什么范围内?
分析 本题考查常见函数的导数及利用导数知识解决实际问题的能力.
解 设这次行车的车速应为x km/h,总费用为y元,则y由一路的耗油费及司机的工资两部分组成.
y=
4分
y′
,令y′=0,得x=
6分
由于x>
时,y′>0,所以函数y=
在x∈［50,100］上是增函数.故最经济的车速是50 km/h.
8分
ymax=
ymin=
即这次行车的总费用在139.8~178.2元之间. 10分