高三数学同步检测(四)
第一章单元检测(B)
说明:本试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填入题后括号内,第Ⅱ卷可在各题后直接作答.共100分,考试时间90分钟.
第Ⅰ卷(选择题共40分)
一、选择题(本大题共10小题,每小题4分,共40分)
1.抛掷2颗骰子,所得点数之和ξ是一个随机变量,则P(ξ≤4)为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
分析 本题考查离散型随机变量和的概率.
解 ξ=2对应(1,1);ξ=3对应(1,2),(2,1);ξ=4对应(1,3),(2,2),(3,1).故ξ=2,3,4时分别对应1,2,3个基本事件.
而整个事件包含36个基本事件,由等可能事件的概率公式,得
P(ξ≤4)=P(ξ=2)+P(ξ=3)+P(ξ=4)=![]() +
+![]() +
+![]() =
=![]() .
.
答案 D
2.一班有学员54人,二班有学员42人,现在要用分层抽样的方法从两个班抽出一部分人参加4×4方队进行军训表演,则一班和二班分别被抽取的人数是( )
A.9人、7人 B.15人、1人
C.8人、8人 D.12人、4人
解析 由题意知,各班所抽人数应按各班所占人数的比例来抽取,一班被抽取的人数为16×![]() =9(人);二班被抽取的人数为16-9=7(人).
=9(人);二班被抽取的人数为16-9=7(人).
答案 A
3.某一天供电网络,有n个用电单位,每个单位在一天中使用电的机会都是p,供电网络中一天平均用电的单位个数是( )
A.np(1-p) B.np C.n D.p(1-p)
解析 因为每天用电单位的个数ξ服从二项分布,所以Eξ=np.
答案 B
4.设随机变量ξ服从正态分布N(0,1),记Φ(x)=P(ξ<x),则下列结论不正确的是( )
A.Φ(0)=0.5 B.Φ(x)=1-Φ(-x)
C.P(ξ<a)=2Φ(a)-1 D.P(ξ>a)=1-Φ(a)
分析 本题考查正态分布的运算.
解 由正态分布的相关概念易知A、B、C正确,P(ξ>a)=1-P(ξ<a)=1-[2Φ(a)-1]=2-2Φ(a).
答案 D
5.有10件产品,其中3件是次品,从中任取两件,若ξ表示取得次品的个数,则Eξ等于( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
分析 本题考查离散型随机变量的数学期望,解题的关键是找到与每个ξ的值相对应的概率P的值.
解 由题意,知ξ取0,1,2,它取每个值的概率都符合等可能事件的概率公式,即
P(ξ=0)=![]() =
=![]() ,
,
P(ξ=1)= ![]() =
=![]() ,
,
P(ξ=2)= ![]() =
=![]() .
.
于是Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() =
=![]() .
.
答案 A
6.从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码,统计结果如下:
| 卡片号码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 取到的次数 | 13 | 8 | 5 | 7 | 6 | 13 | 18 | 10 | 11 | 9 |
则取到号码为偶数的频率是( )
A.0.53 B.0.5 C.0.47 D.0.37
解析 ![]()
答案 C
7.★某公司有5万元资金用于投资开发项目,如果成功,一年可获利12%;一旦失败,一年后将丧失全部资金的50%.下表是过去100例类似项目开发的实施结果:
| 投资成功 | 投资失败 |
| 96次 | 4次 |
则该公司一年后估计可获收益的期望是( )
A.4 000元 B.4 520元
C.25 000元 D.4 760元
分析 本题考查概率的基本知识和数学期望概念,应用概率知识解决实际问题的能力.
解 收益的期望为5×12%×![]() -5×50%×
-5×50%×![]() =0.476 0(万元)=4 760(元).
=0.476 0(万元)=4 760(元).
答案 D
8.每次从0~9这10个数字中随机取一个数字(取后放回),连续取n次,得到n个数字组成的数字序列.若使该序列中的数字6至少出现一次的概率为0.8,则n的最小值是( )
A.14 B.15 C.16 D.17
分析 本题考查等可能性事件概率的应用.
解 有放回地排列n个数字,得10n个基本事件,其中不含6的基本事件为9n.由题意得![]() ≥0.8,
≥0.8,
即0.9n≤0.2,∴n≥![]() ≈15.3.
≈15.3.
∴n最小取16.
答案 C
9.已知随机变量ξ~B(9,![]() ),则使P(ξ=k)取得最大值的k值为 ( )
),则使P(ξ=k)取得最大值的k值为 ( )
A.2 B.3 C.4 D.5
分析 ξ~B(n,p)为二项分布,要熟记二项分布的公式P(ξ=k)=![]() pk(1-p)n-k,求P(ξ=k)的最大值,还要注意对不等式组
pk(1-p)n-k,求P(ξ=k)的最大值,还要注意对不等式组![]() 的运算.
的运算.
解 ∵ξ服从二项分布,
∴P(ξ=k)=![]() (
(![]() )k(
)k(![]() )9-k,
)9-k,
要使P(ξ=k)最大,则只需
![]() 即
即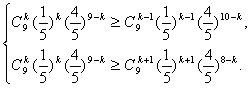
解得k=2.
答案 A
10.右图是当σ取三个不同值σ1、σ2、σ3的三种正态曲线N(0,σ2)的图,那么σ1、σ2、σ3的大小关系是( )
A.σ1>1>σ2>σ3>0 B.0<σ1<σ2<1<σ3
C.σ1>σ2>1>σ3>0 D.0<σ1<σ2=1<σ3
分析 本题考查正态曲线的性质.
解 由正态曲线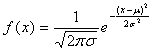 ,可知
,可知
当μ=0时,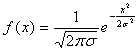 .
.
令x=0,得![]() .
.
当σ=1时,![]() ;
;
当0<σ<1时,它与y轴交点的纵坐标大于f(0);
当σ>1时,它与y轴交点的纵坐标小于f(0).
答案 D
第Ⅱ卷(非选择题共60分)
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
11.设一次试验成功的概率为p,现进行16次独立重复试验.当p= 时,成功次数的标准差最大,其最大值为 .
分析 本题考查服从二项分布的随机变量的标准差.解题的关键是构造目标函数.
解 由于成功的次数ξ服从二项分布,所以Dξ=npq=16p(1-p).
∴σξ=16p(1-p)=4p(1-p)≤4×p+1-p[]2=2.
当且仅当p=1-p,即p=1[]2时取等号,此时(σξ)max=2.
另解 σξ=![]() ,
,
 ∵0≤p≤1,∴当p=
∵0≤p≤1,∴当p=![]() 时,(σξ)max=2.
时,(σξ)max=2.
答案 ![]() 2
2
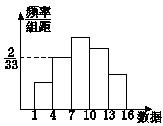
12.右图是一样本的频率分布直方图,其中(4,7)内的频数为4,数据在[1,4)∪[7,16)内的频率为 ,样本容量为 .
分析 本题考查一样本在给定区间内的频率及该样本的容量.注意用相应的直方图面积来表示在各个区间内取值的频率时,所有小矩形的面积和等于1.
解 在(4,7)内的频率为P1,且![]() =
=![]() ,
,
所以P1=![]() .
.
所以数据在[1,4)∪[7,16)内的频率为![]() .
.
设样本容量为n,则![]() =
=![]() ,解得n=22.
,解得n=22.
答案 ![]() 22
22
13.一批产品,分为一、二、三级,其中一级品是二级品的两倍,二级品是三级品的两倍,从这批产品中随机抽取一个检验质量,其级别为随机变量ξ,则ξ的分布列为 及P(ξ>1)= .
解析 由题意知ξ=1,2,3.ξ取1,2,3的概率依次是4a,2a,a,因为4a+2a+a=1,所以a=![]() ,即ξ取1,2,3的概率依次是
,即ξ取1,2,3的概率依次是![]() ,
,![]() ,
,![]() .
.
答案 分布列为
| ξ | 1 | 2 | 3 |
| P |
|
|
|
P(ξ>1)=![]() .
.
14.将参加数学竞赛的1 000名学生编号如下:0 001,0 002,0 003,…,1 000,打算从中抽取一个容量为50的样本,按系统抽样的方法分成50个部分,如果第一部分编号为0 001,0 002,0 003,…,0 020,在第一部分随机抽取一个号码为0 015,则抽取的第40个号码为.
解析 由系统抽样的要求可知,所抽取的号码是首项为a1=0 015,公差为d=20的等差数列.所以a40=a1+(40-1)d=0 015+39×20=0 795.
答案 0 795
三、解答题(本大题共5小题,共44分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分8分)进行某种试验,设试验成功的概率为![]() ,失败的概率为
,失败的概率为![]() ,以ξ表示试验首次成功所需试验的次数,试写出ξ的分布列,并计算ξ取偶数的概率.
,以ξ表示试验首次成功所需试验的次数,试写出ξ的分布列,并计算ξ取偶数的概率.
分析 本题考查如何布列离散型随机变量的分布列,以及如何求它的和的概率.其中ξ=k表示前(k-1)次试验失败而第k次试验成功这一事件,ξ服从几何分布.它是相互独立事件同时发生的概率模型.设事件A1,A2,…,An相互独立,那么这n个事件同时发生的概率等于每个事件发生的概率的积,即P(A1·A2·…·An)=P(A1)·P(A2)·…·P(An).
解 随机变量ξ的取值是1,2,3,…,k,…. 2分
∵P(ξ=1)=![]() ,
,
P(ξ=2)=![]() ·(
·(![]() ),
),
P(ξ=3)=![]() ·(
·(![]() )2,
)2,
…
P(ξ=k)=![]() ·(
·(![]() )k-1,
)k-1,
…
| ξ | 1 | 2 | 3 | … | K | … |
| P |
|
|
| … |
| … |
∴ξ的分布列为
5分
取偶数的概率为
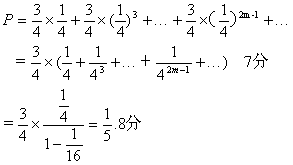
16.(本小题满分8分)人寿保险中的某一年龄段,在一年的保险期内,每个被保险人需交纳保险费a元,被保险人意外死亡则保险公司赔付3万元,出现非意外死亡则赔付1万元.经统计此年龄段一年内意外死亡的概率为p1,非意外死亡的概率为p2,则保险费a需满足什么条件,保险公司才可能盈利?
分析 本题考查离散型随机变量的期望在现实生活中的应用.
要使保险公司盈利,需使它所收总保险费大于总赔付费,即它的期望大于零.解题的关键是列出分布列,求出数学期望.
解 设ξ为保险公司对每一投保人的盈利数,则ξ的可能取值为a,a-30 000,a-10 000. 2分
且P(ξ=a)=1-p1-p2,
P(ξ=a-30 000)=p1,
P(ξ=a-10 000)=p2. 5分
随机变量ξ的概率分布列为
| ξ | A | a-30 000 | a-10 000 |
| P | 1-p1-p2 | p1 | p2 |
6分
Eξ=a(1-p1-p2)+(a-30 000)p1+(a-10 000)p2
=a-30 000p1-10 000p2.
保险公司要盈利,必须使Eξ>0.于是a>30 000p1+10 000p2.8分
[]17(本小题满分8分)从全校参加科技知识竞赛的学生试卷中,抽取一个样本,考察竞赛的成绩分布.将样本分成5组,绘成频率分布直方图(如右图),图中从左到右各小组的小长方形的高的比是1∶3∶6∶4∶2,最右边一组的频数是6.
请结合直方图提供的信息,解答下列问题:
(1)样本的容量是多少?
(2)列出频率分布表;
(3)成绩落在哪个范围内的人数最多?并求该小组的频数、频率;
(4)估计这次竞赛中,成绩不低于60分的学生占总人数的百分率.
分析 当样本中的个体取不同的值较多时,通常用频率分布直方图的面积来表示各个区间内取值的概率,所有小矩形的面积之和等于1.
解 (1)由于各组的组距相等,所以各组的频率与各小长方形的高成正比且各组频率的和等于1,那么各组的频率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .设样本容量为n,则
.设样本容量为n,则![]() =
=![]() ,所以样本容量n=48.
,所以样本容量n=48.
2分
(2)
| 成绩 | 频数 | 频率 |
| 50.5~60.5 | 3 |
|
| 60.5~70.5 | 9 |
|
| 70.5~80.5 | 18 |
|
| 80.5~90.5 | 12 |
|
| 90.5~100.5 | 6 |
|
| 合计 | 48 | 1 |
5分
(3)成绩落在70.5~80.5之间的人数最多,该组的频数和频率分别是18和![]() . 6分
. 6分
(4)不低于60分的学生占总人数的百分率为1-![]() ≈94%. 8分
≈94%. 8分
18.(本小题满分10分)设一汽车在前进途中要经过4个路口,汽车在每个路口遇到绿灯的概率为![]() ,遇到红灯(禁止通行)的概率为
,遇到红灯(禁止通行)的概率为![]() .假定汽车只在遇到红灯或到达目的地才停止前进,ξ表示停车时已经通过的路口数,求:
.假定汽车只在遇到红灯或到达目的地才停止前进,ξ表示停车时已经通过的路口数,求:
(1)ξ的概率的分布列及期望Eξ;
(2)停车时最多已通过3个路口的概率.
分析 本题重点考查概率与分布的基础知识.正确确定随机变量的所有可能取值以及取每一个值的概率是解决本题的关键.
解 (1)ξ的所有可能值为0,1,2,3,4.
用Ak表示“汽车通过第k个路口时不停(遇绿灯)”,
则P(Ak)=![]() (k=1,2,3,4),且A1,A2,A3,A4独立.
(k=1,2,3,4),且A1,A2,A3,A4独立.
故P(ξ=0)=P(![]() )=
)=![]() ,
2分
,
2分
P(ξ=1)=P(A1·![]() )=
)=![]() ×
×![]() =
=![]() ,
,
P(ξ=2)=P(A1·A2·![]() )=(
)=(![]() )2×
)2×![]() =
=![]() ,
,
P(ξ=3)=P(A1·A2·A3·![]() )=(
)=(![]() )3×
)3×![]() =
=![]() ,
,
P(ξ=4)=P(A1·A2·A3·A4)=(![]() )4=
)4=![]() . 5分
. 5分
从而ξ有分布列
| ξ | 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
6分
Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() +4×
+4×![]() =
=![]() . 8分
. 8分
(2)P(ξ≤3)=1-P(ξ=4)=1-![]() =
=![]() .
.
答:停车时最多已通过3个路口的概率为![]() .
10分
.
10分
19.(本小题满分10分)某5名学生的数学和化学成绩如下表:
|
学科 | A | B | C | D | E |
| 数学成绩(x) | 88 | 76 | 73 | 66 | 63 |
| 化学成绩(y) | 78 | 65 | 71 | 64 | 61 |
(1)画出散点图;
(2)求化学成绩(y)对数学成绩(x)的回归直线方程.
分析 本题考查如何求回归直线的方程.分清自变量与因变量是正确解题的关键.
解 (1)
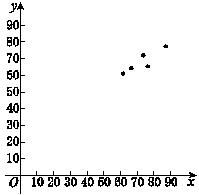 3分
3分
(2)
| 序号 | x | Y | x2 | y2 | xy |
| 1 2 3 4 5 | 88 76 73 66 63 | 78 65 71 64 61 | 7 744 5 776 5 329 4 356 3 969 | 6 084 4 225 5 041 4 096 3 721 | 6 864 4 940 5 183 4 224 3 843 |
| ∑ | 366 | 339 | 27 174 | 23 167 | 25 054 |
5分
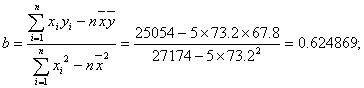
![]() 9分
9分
所以y对x的回归直线方程为![]() =0.62x+22.06.
10分
=0.62x+22.06.
10分