06年高三年级四月份单科教学质量检查测试数学（理工类）
本试题分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟。
第Ⅰ卷(选择题 共60分)
一、选择题：本大题共12小题.每小题5分;共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
A.
B.
C.
D.
2.对任意实数x,下列函数中的奇函数是
A.
B.
C.
D.
3.已知a、b、c为直线，α、β、γ为平面，则下列命题中正确的是
A．
⊥γ，β⊥γ
∥β
B．a⊥b,a⊥c,
⊥α
C．a⊥,b⊥β, ∥β
a∥b D．a∥,b⊥ab⊥
4.若把一个函数的图象按
平移后得到y=cosx的图象.则原图象的函数解析式为
A.
B.
C.
D.
5.已知R为全集,A=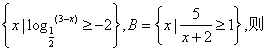
(RA)∩B是
A.
B.
C.
D.
6.平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,∠BCD=90°,∠BAA1=∠DAA1=60°,则对角线A1C的长为
A.
B.
C.
D.
7.下表给出一个“直角三角形数阵”
……
满足每一列成等差数列，从第三行起，每一行的数成等比数列，且每一行的公比相等，记第i行等j列的数为
A．
B．
C．
D．1
8．如果
t
A．
B．-
C．
D．
9．直线
是直线l1⊥l2的
A．充要条件 B．既不充分也不必要条件
C．必要不充分条件 D．充分不必要条件
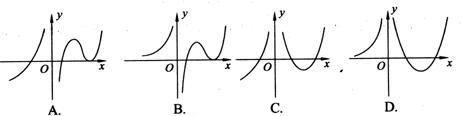
10．设函数f(x)在定义域内可导，y=f(x)的图象如右图，则导函数
的图象可能为下图中的 x
11．某公司新招聘进8名员工，平均分配给下属的甲、乙两个部门，其中两名英语翻译人员不能分在同一个部门，另外三名电脑编程人员也不能分在同一个部门，则不同的分配方案共有
A．36种 B．38种 C．108种 D．24种
12．已知F1、F2分别是双曲线
的左、右焦点，P为双曲线上一点，过F1作∠F1PF2的平分线的垂线，垂足为H.则点H的轨迹为
A.椭圆 B.双曲线 C.圆 D.抛物线
tx第Ⅱ卷(非选择题 共90分)
注意事项:
1. 第卷共6页,用蓝色或黑色钢笔、圆珠笔直接写在试题卷中.
2. 答卷前将密封线内的项目填写清楚.
二、填空题：本大题共4个小题.每小题4分;共16分.把答案填写在题中的横线上.
13.对于函数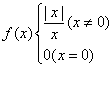
,给定下列四个命题:
①
②
③
④
其中正确命题的序号是_____________.
14.若(
)n展开式的第4项含
,则n的值为__________.
15.已知抛物线
的焦点为F,AB是过焦点F的弦,且AB的倾斜角为30°,则△OAB的面积为____________.
16.已知A、B、C是半径为1的球面上的三点，A、B两点和A、C两点的球面距离都是
，B、C两点的球面距离为
，则球心到平面ABC的距离为___________.
三、解答题：本大题共6小题.共74分.解答应写出文字说明、证明过程或演算步骤.
17. (本小题满分12分)
在△ABC中,已知
(1) 求证,a、b、c成等差数列；
(2) 求角B的取值范围.
18.(本小题满分12分)
现在甲、乙两只暗色口袋，已知甲口袋中装有白球2个，黑球2个，乙口袋内装有白球2个和黑球3个，且所有球只有颜色不同，其大小均相同.现从甲、乙两个口袋中各取1球交换后放回袋中.
(1) 求甲口袋中恰有2个白球的概率;
(2) 求甲口袋内白球数的数学期望.
19.(本小题满分12分)
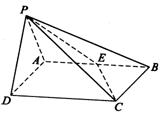如图,在四棱锥P-ABCD中,侧面PAD是正三角形且与底面ABCD垂直,底面ABCD是矩形,E是AB中点,PC与平面ABCD所成角为30°.
(1) 求二面角P—CE—D的大小;
(2) 当AD为多长时,点D到平面PCE的距离为2.
20.(本小题满分12分)
已知:命题
是
的原函数,且
命题q:集合
A∩B=φ.
(1) 求不等式
(2) 求使命题p、q中有且只有一个真命题时实数a的取值范围.
21.(本小题满分12分)
已知数列
的首项
,前n项的和Sn满足关系式
(1) 求证:数列是等比数列;
(2) 设数列的公比为f(t),作数列
(3) 求
…
的和.
22.(本小题满分14分)
已知点G是ΔABC的重心,A(0,-1),B(0,1).在x轴上有一点M，满足
（1）求点C的轨迹方程；
（2）若斜率为k的直线l与点C的轨迹交于不同两点P，Q，且满足
试求k的取值范围.
数学(理工类)参考答案
一、1—12 BCCDBCCBDDAC
二、13．①② 14. 9 15.4 16.
三、17.解：（1）由条件得：
∴
∴
∴
∴a、b、c成等差数列.
(2) ∵
∵
∴
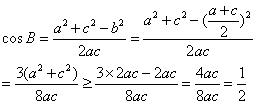
18.解：（1）甲、乙两口袋中各取1球交换后，甲口袋恰有2个白球有二种情况：
①都交换的是白球，则P（A1）=
②都交换的是黑球，则P（A2）=
（2）设甲口袋内白球数ξ的分布列：
| ξ | 1 | 2 | 3 |
| P |
|
|
|
∴Eξ=
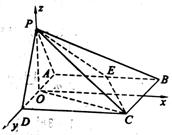19．解：（1）取AD的中点O，连接PO.
∵△PAD是正三角形 ∴PO⊥AD
s
又面PAD⊥面ABCD ∴PO⊥面ABCD
以O为原点,过O作AB平行线为x轴,OD为y轴,OP为z轴建立空间直角坐标系,连OC,则∠PCO为PC与面ABCD所成角
∴∠PCO=30°
设AD=a,则PO=
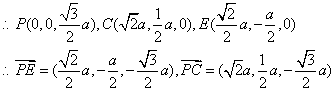
设平面PCE的法向量为
则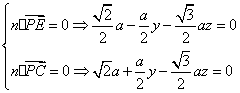
∴
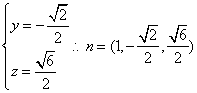
又面DEC的法向量为
∴
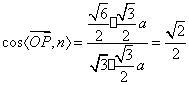
∴二面角P-CE-D为45°
（2）D（0，
，0）则
∴D到面PCE的距
20．（1）解：∵
由
(2)设
此时
∴
当
≥0时,由A∩B=φ
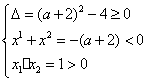
解得
综上可得
①要使p真q假,则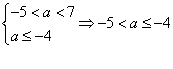
②要使p假q真,则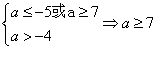
∴当a的取值范围为(-5,-4]∪［7,+∞)时,命题p、q中有且只有一个为真命题.
21.解：（1）S1=
∴
∴
同理
又
∴
∴
∴为以1为首项，公比为
的等比数列.
(2)
∴
∴
(3)由知
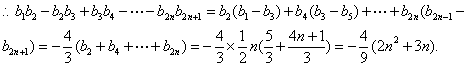
22.(1)设C(x,y)，则G
∴
∥AB.
又M是x轴上一点,则M(
).
又
∴
整理得
即为曲线C的方程.
(2)①当k=0时,l和椭圆C有不同两交点P、Q，根据椭圆对称性有
②当k
0,可设l的方程为
联立方程组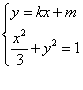
消去y,整理得
∵直线l和椭圆C交于不同两点，
∴
即
设
则
是方程（*）的两相异实根，
则PQ的中点N
的坐标是
即N（
）.
又
⊥
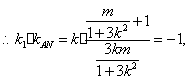
代入(* *)得
即
∪(0,1)
结合①②得,k的取值范围是(-1,1).