07届高复小题训练(4)
姓名: 班级:
一![]() 选择题:本大题共有10小题,每小题5分,共50分
选择题:本大题共有10小题,每小题5分,共50分![]() 在每小题给出的四个选项有且只有一项是符合题目要求的
在每小题给出的四个选项有且只有一项是符合题目要求的![]()
1.“![]() ”是“
”是“![]() 且
且![]() ”的
”的
A![]() 充分不必要条件 B
充分不必要条件 B![]() 必要不充分条件
必要不充分条件
C![]() 充要条件 D
充要条件 D![]() 既不是充分条件,也不是必要条件
既不是充分条件,也不是必要条件
2.设![]() 与
与![]() 是两个不共线的向量,且向量
是两个不共线的向量,且向量![]() 与
与![]() 共线,则
共线,则![]() =
=
A![]() 0 B
0 B![]()
![]() C
C![]()
![]() D
D![]()
![]()
3.函数![]() 是奇函数,则
是奇函数,则![]() 等于
等于
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
4.函数![]() 的图象按向量
的图象按向量![]() 平移后,所得的图象对应的函数的解析式是
平移后,所得的图象对应的函数的解析式是![]() ,则
,则![]() 等于
等于
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
5.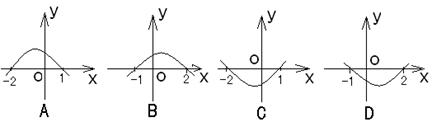 不等式
不等式![]() 的解集为
的解集为![]() ,则函数
,则函数![]() 的图象为
的图象为
6.某人为了观看2008年奥运会,从2001年起,每年5月10日到银行存入a元定期储蓄,若年利率为p且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年将所有的存款及利息全部取回,则可取回的钱的总数(元)为(不计利息税)
A![]()
![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
7.函数![]() 在区间
在区间![]() 上有最小值,则函数
上有最小值,则函数![]() 在区间
在区间![]() 上一定
上一定
A![]() 有最小值 B
有最小值 B![]() 有最大值 C
有最大值 C![]() 是减函数 D
是减函数 D![]() 是增函数
是增函数
8.设函数![]() 是定义在
是定义在![]() 上以3为周期的奇函数,若
上以3为周期的奇函数,若![]() ,
,![]() ,则
,则
A![]()
![]() B
B![]()
![]() 且
且![]() C
C![]()
![]() 或
或![]() D
D![]()
![]()
9.若某等差数列![]() 中,
中,![]() 为一个确定的常数,则其前
为一个确定的常数,则其前![]() 项和
项和![]() 中也为确定的常数的是
中也为确定的常数的是
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
10.函数![]() 的图象的一条对称轴方程为
的图象的一条对称轴方程为![]() ,则直线
,则直线![]() 的倾斜角是
的倾斜角是
A![]() 45° B
45° B![]() 135° C
135° C![]() 60°
D
60°
D![]() 120°
120°
二![]() 填空题:本大题共6小题,每小题5分,共30分
填空题:本大题共6小题,每小题5分,共30分![]() 把答案填写在答题卡相应位置上
把答案填写在答题卡相应位置上![]()
11.定义运算![]() 为:
为:![]() ,例如,
,例如,![]() ,则函数
,则函数![]() 的值域
的值域
12.数列![]() 是等差数列
是等差数列![]() ,则n的值为
,则n的值为
13.向量![]()
![]()
![]() 为单位向量,且
为单位向量,且![]() ,则
,则![]() 与
与![]() 的夹角为
.
的夹角为
.
14.已知函数![]() 为奇函数,函数
为奇函数,函数![]() 为偶函数,且
为偶函数,且![]() ,则
,则![]() =
=
15.已知函数![]() ,若对任意
,若对任意![]() 有
有![]() 成立,则方程
成立,则方程![]() 在
在![]() 上的解为 _____________
上的解为 _____________ ![]()
16.已知![]() 满足
满足![]() ,
,![]() ,则
,则
![]() _____________.
_____________.
答案:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
11、 12、 13、
14、 15、 16、
附加题:已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,且
,且![]()
![]()
(1) 求k的值;
(2) 求![]() ;
;
(3) 是否存在正整数![]() ,使
,使![]() 成立?若存在,求出这样的正整数;若不存在,说明理由.
成立?若存在,求出这样的正整数;若不存在,说明理由.
一![]() 选择题:每小题5分,共60分
选择题:每小题5分,共60分![]()
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 | B | D | D | B | B | D | D | D | B | B |
二![]() 填空题:每小题5分,共30分
填空题:每小题5分,共30分![]()
11![]() [-1,
[-1,![]() ] 12
] 12![]() 15 13
15 13![]() 120度 14
120度 14 ![]() 15.
15. ![]() 16. 24
16. 24
附加题:解:(1) ![]()
又![]() ,∴
,∴![]()
![]() ………………3分
………………3分
(2) 由 (1) 知
![]() ①
①
当![]() 时,
时,![]() ②
②
①-②,得![]() ………………6分
………………6分
又![]() ,易见
,易见![]()
于是![]() 是等比数列,公比为
是等比数列,公比为![]() ,所以
,所以
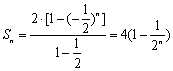 ………………8分
………………8分
(3) 不等式![]() ,即
,即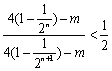 .
.
整理得![]() …………12分
…………12分
假设存在正整数![]() 使得上面的不等式成立,由于2n为偶数,
使得上面的不等式成立,由于2n为偶数,![]() 为整数,则只能是
为整数,则只能是![]()
![]() ………………14分
………………14分
因此,存在正整数![]() .……16分
.……16分