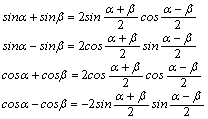试卷类型：A

襄樊市高三年级统考试题

数　 学

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分，考试时间120分钟．

第 Ⅰ 卷 (选择题，共60分)

注意事项：

1．请考生将自己的姓名、学号、班级填写在第Ⅱ卷的密封线内．

2．每小题选出答案后用2B铅笔把答题卡上对应题目的答案代号涂黑，如需改动，必须用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．

3．考试结束后，监考人员将本试卷和答题卡一并收回．

正棱台、圆台侧面积公式： 台体体积公式：

参考公式：

三角函数和差化积公式：

一．选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1.　　集合P＝{1，a}，a²是集合P中的元素，则a可取值有：
　　A．1个　　　　　　　　　　　B．2个　　　　　　　　　　　　C．3个　　　　　　　　　　 D．4个

2.　　直线(3m＋2)x－(2m－1)y＋5m＋1＝0必过定点
　　A．(－1，1)　　　　　　　 B．(1，1)　　　　　　　　　　 C．(1，－1)　　　　　　　D．(－1，－1)

3.　　已知双曲线的离心率e＜2，则k的取值范围是
　　A．k＜0或k＞3　　　　 B．－3＜k＜0　　　　　　　 C．－12＜k＜0　　　　 D．－8＜k＜3

4.　　已知tg110°＝a，则tg50°的值为
　　A．　　　　　　　B．　　　　　　　　C．　　　　　　 D．

5.　　若复数的辐角主值为，则复数－2－i的辐角主值是
　　A．　　　　　　　　 B．　　　　　　　　　C．　　　　　　　　D．

6.　　数列是公差不为零的等差数列，并且a₅，a₈，a₁₃是等比数列的相邻三项，若，则
　　A．　　　　　　　B．　　　　　　　　C．　　　　　　 D．

7.　　国际乒乓球赛的用球已由“小球”改为“大球”，“小球”的直径为38mm，“大球”的直径为40mm，则“小球”的体积与“大球”的体积之比为
　　A．　　　　　 B．19∶20　　　　　　　　　　C．19²∶20²　　　　　　　D．19³∶20³

8.　　椭圆的焦点F₁和F₂，点P在椭圆上，如果线段PF₁的中点在y轴上，那么 PF₁ ∶ PF₂ 的值为
　　A．7∶1　　　　　　　　　　 B．5∶1　　　　　　　　　　　 C．9∶2　　　　　　　　　　D．8∶3

9.　　已知的展开式的第七项为，则
　  A．　　　　　　　　　　B．　　　　　　　　　　　　　C．　　　　　　　　　 D．

10. (理科考生做)图中多面体是经过正四棱柱底面顶点B作截面A₁BC₁D₁而截得的，已知AA₁＝CC₁，截面A₁BC₁D₁与底面ABCD成45°的二面角，AB＝1，则这个多面体的体积为
　　A．　　　　　　　　　　B．
　　C．　　　　　　　　　　D．
　　　 (文科考生做) 一个圆锥的底半径为3，两条母线的最大夹角为60°，则这个圆锥的内切球的表面积是
　　A．3　　　　　　　　　　　B．6　　　　　　　　　　　　 C．12　　　　　　　　　 D．24

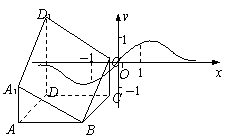
11. (理科考生做)函数的大致图象如图所示，则
　　A．a∈(－1，0)　　　　 B．a∈(0，)
　　C．a∈(，1)　　　　　D．a∈(1，＋∞)
　　　 (文科考生做)设函数f (x)＝ax²＋bx＋c对任意实数t都有f (2＋t)＝ f (2－t)成立，在函数值f (－1)，f (1)，f (2)，f (5)中的最小的一个不可能是
　　A．f (－1)　　　　　　　　　B．f (1)　　　　　　　　　　　　C．f (2)　　　　　　　　　　D．f (5)

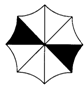
12. (理科考生做)如图，某伞厂生产的“太阳”牌太阳伞的伞蓬是由太阳光的七种颜色组成，七种颜色分别涂在伞蓬的八个区域内，且恰有一种颜色涂在相对区域内，则不同的颜色图案的此类太阳伞至多有
　　A．40320种　　　　　　　 B．5040种
　　C．20160种　　　　　　　 D．2520种
　　　 (文科考生做)商场开展促销抽奖活动，摇奖器摇出一组中奖号码是8、2、5、3、7、1．参加抽奖的每位顾客从0－9这十个号码中任意抽出六个组成一组，如果顾客抽出的六个号码中至少有5个与摇出的号码相同(不计顺序)就可以得奖．一位顾客可能抽出的不号码共有m组，其中可以中奖的号码共有n组，则的值为
　　A．　　　　　　　　　　　 B．　　　　　　　　　　　　C．　　　　　　　　　　 D．

襄樊市高三年级统考试题(2003.3)

数　　 学

第 Ⅱ 卷 (非选择题，共90分)

注意事项：

第Ⅱ卷共6页，用黑色签字笔直接答在试题卷中，答卷前将密封线内的项目填写清楚．

题 号	一	二	三						总　 分
			17	18	19	20	21	22
得 分

得分	评卷人

二．填空题：本大题共4小题，每小题4分，共16分。将正确答案填在题中横线上．

13. 不等式x²≤ x＋2 的解集是　　　　　　　　　　　　　．

14. AB是抛物线y＝x²的一条弦，若AB的中点到x轴的距离为1，则弦AB长度的最大值为　　　　　　　．

15. 设函数，则满足的x值为______________．

16. 一同学在电脑中打出如下若干个圆（图中●表示实圆，○表示空心圆）：
　　　　　　●○●●○●●●○●●●●○●●●●●○●●●●●●○
若将此若干个圆依次复制得到一系列圆，那么在前2002个圆中，有　　　　 个空心圆．

三．解答题：本大题共6小题，满分74分．

得分	评卷人

17. (本大题满分12分)已知函数(a＞0)的图象经过点A(0，1)，B(，1)，当时f (x)的最大值为．
　　(1)求f (x)的解析式；
　　(2)将f (x)的图象经过平移变换可得到一个奇函数y＝g (x)的图象，请写出你的变换过程和g (x)的表达式．

得分	评卷人

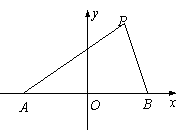
18. (本大题满分12分) 如图，在平面直角坐标系中，已知点A(－2，0)，B(2，0)，动点P满足 PA － PB = ．

　　(1)求点P的轨迹E的方程；
　　(2)是否存在过点B的直线l与曲线E交于点M、N，且 BM ＝2 BN ？若存在，求出直线l的方程；若不存在，说明理由．

19. (本大题满分12分)

　　(理科考生做)已知正方体ABCD－A₁B­₁C₁D₁的棱长为a，E为棱C₁C上的动点．

(1)求异面直线DB与A₁E所成角的大小；
(2)若二面角A₁－DB－E为直二面角，求E点的位置；
(3)求满足(2)时，四面体B－A₁DE的体积．

　　(文科考生做)已知正方体ABCD－A₁B­₁C₁D₁的棱长为a，E为棱C₁C的中点．

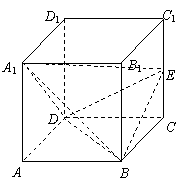　　(1)证明：直线DB⊥直线A₁E；
(2)求二面角A₁－DB－E的大小；
(3)求四面体B－A₁DE的体积．

得分	评卷人

20. (本大题满分12分)国际上常用恩格尔系数（记作n）来衡量一个国家和地区人民生活水平的状况，它的计算公式为：
　　　　　 
　　各种类型家庭的n如下表所示：

家庭类型	贫　困	温　饱	小　康	富　裕	最富裕
n	n＞60%	50%＜n≤60%	40%＜n≤50%	30%＜n≤40%	n≤30%

　　根据某市城区家庭抽样调查统计，1996年至2001年间，每户家庭消费支出总额每年平均增加680元，其中食品消费支出总额每年平均增加100元．
　　(1)若1996年该市城区家庭刚达到小康，且该年每户家庭消费支出总额为8600元，问2001年能否达到富裕？请说明理由；
　　(2)若2001年比1996年的消费支出总额增加34%，而其中食品消费支出总额增加10%，问从哪一年起能达到富裕？请说明理由．

得分	评卷人

21. (本大题满分12分)已知数列中，， (n∈N)，数列对任何n∈N都有．
　　(1)求证为等比数列；
　　(2)求的通项公式；
　　(3)设数列的前n项和为S_n，求．

得分	评卷人

22. (本大题满分14分)

　　(理科考生做)已知二次函数满足．
　　(1)若，证明的图象与x轴有两个交点，且这两个交点间的距离d满足不等式：；
　　(2)设f (x)在(t＞0且t≠1)处取得最小值，且对任意实数x，等式
　　　　  　(其中n∈N，g (x)为关于x的多项式)
都成立，试用t表示a_n和b_n；
　　(3)求．

得分	评卷人

(文科考生做)定义域为R的函数f (x)满足：对任意x，y∈R，均有f (x＋y)＝f (x)＋f (y)－3，且，当>0时，．
　　(1)试举出一个具有这种性质的一个函数；
　　(2)判断函数的单调性，并给出证明；
　　(3)解不等式：f (x²＋x－3)＋3＜0．

高三数学参考答案及评分标准

一．选择题：BACAC　ADAA(理(文

二．填空题：13．{x｜－1≤x≤2}　　14．　　15．2　　16．445

三．解答题：

17．(1)解：由已知得：　∴a＝b 　　　　　　　　　　　　　　　　　　　　　　　　　　2分
　　∴　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分
　　又　∴　　　　　　　　　　　　　6分
　　故a＝2，c＝－1
　　∴ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　8分

(2)解：
　　∴先将的图象向右平移个单位，再向上平移1个单位，即得到奇函数的图象．　　 12分

18．(1)解：由 PA － PB = ＜ AB 知点P的轨迹是以A、B为焦点的双曲线靠近点B的一支，a＝，c＝2，b²＝c²－a²＝2
　　∴点P的轨迹E的方程为： (x≥)　　　　　　　　　　　　　　　　　　　　 4分

(2)解：由题意，直线l与x轴不平行．
　　设l的方程为y=k(x－2)，代入双曲线方程消去x并整理得：
　　　　①
　　设M(x₁，y₁)，N(x₂，y₂) (y₁＞y₂)，则y₁，y₂是方程①的两根
　　∴　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分
　　∵ BM ＝2 BN 　　∴y₁＝－2y­₂
　　故
　　两式相除得：，∴
　　解得： 或 k = 0 (舍去)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 10分
　　这时

∴所求直线方程为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

19．(理)(1)证：由于A₁A⊥面AC，EC⊥面AC，
　　∴AC是A₁E在底面AC上的射影
　　∵BD⊥AC，∴BD⊥A₁E
　　即DB与A₁E所成角为90°．　　　　　　4分
　　(2)解：在正△A₁DB中，BD⊥A₁O，又BD⊥A₁E
 　 ∴BD⊥平面A₁OE　Þ　BD⊥OE
　　故∠A₁OE是二面角A₁－BD－E的平面角
　　∴∠A₁OE＝90°　　　　　　　　　　　  6分
　　设CE＝x，则　
　　
　　∴
　　解得：
　　∴E是CC₁的中点．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

(3)解：面A₁BD⊥面BDE，A₁O⊥BD　　∴A₁O⊥面BDE
 
∴　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

(文)(1)同理(1)
　　(2)解：∵A₁D＝A₁B，∴BD⊥A₁O，同理　BD⊥OE
　　故∠A₁OE是二面角A₁－BD－E的平面角　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分
　　
　　
　　由于，即A₁E²＝OE²＋A₁O²
　　∴A₁O⊥OE，即二面角A₁－DB－E的大小为90°．　　　　　　　　　　　　　　　　　　　　8分
　　(3)同理(3)

20．(1)解∵食品消费支出总额为8600×50%=4300元，　　　　　　　　　　　　　　　　　 2分
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分
　　∴2001年能达到富裕．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

(2)设1996年的消费支出总额为a元，其中食品消费支出总额为b元，
　　则，
　　∴a＝10000，b＝5000　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　9分
　　而经过5年，
　　经过6年，　
　　故到2002年达到富裕．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

21．(1)证：由已知得：
　　
　　若b_n＝0，则
　　∴，不满足条件．
　　故，即为等比数列．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分

(2)解：
　　∴　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

(3)解：，又
　　∴　　　　　　　　　　　　　　10分
　　
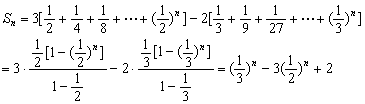
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

22．(理)(1)证：由f (1)＝0得a＋b＋c＝0
　　 (∵a＞c)
　　∴f (x)的图象与x轴有两个不同的交点．　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2分
　　由知，一个交点的横坐标为1，设另一个交点的横坐标为x₁，
　　则
　　由a＋b＋c＝0 及a＞b＞c知a＞0，c＜0
　　a＝－b－c＜－2c　Þ　，c＝－a－b＞－2a　Þ　
　　∴，即　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

(2)解：由
　　在 中令x＝1得：　　①
　　令得：　　 ②
　　②－①得：，∴　　　　　　　　　　　　　　　　　　　　　10分

(3)解：
　　当t＞1时，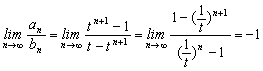
　　当0＜t＜1时，．　　　　　　　　　　　　　　　　　　　　　　　　 14分

(文)(1)解：函数f (x)＝－2x＋3满足条件．　　　　　　　　　　　　　　　　　　　　　　　　　　　4分

(2)设x₁＜x₂，则由f (x＋y)＝f (x)＋f (y)－3得：
　　f (x₁＋x₂－x₁)＝f (x₁)＋f (x₂－x₁)－3，即f (x₂)－f (x₁)＝f (x₂－x₁)－3
　　又
　　∴ f (x₂)－f (x₁)＝f (x₂－x₁)－3＝f (x₂－x₁＋)
　　∵x₁＜x₂　∴，因此f (x₂－x₁＋)＜0
　　即f (x₂)－f (x₁)　Þ　 f (x₂)＜f (x₁)
　　∴函数f (x)是减函数．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　10分

(3)解：在f (x＋y)＝f (x)＋f (y)－3中令得：f (3)＝－3
　　∴不等式即　f (x²＋x－3)＜f (3)
　  ∵f (x)是减函数，∴x²＋x－3＞3，解得：x＜－3　或 x＞2
　　∴不等式的解集是{x｜x＜－3或x＞2}．　　　　　　　　　　　　　　　　　　　　　　　　　　　　 14分