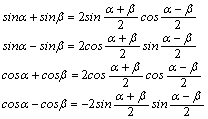试卷类型：A
襄樊市高三年级统考试题
数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分，考试时间120分钟．
第 Ⅰ 卷 (选择题，共60分)
注意事项：
1．请考生将自己的姓名、学号、班级填写在第Ⅱ卷的密封线内．
2．每小题选出答案后用2B铅笔把答题卡上对应题目的答案代号涂黑，如需改动，必须用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．
3．考试结束后，监考人员将本试卷和答题卡一并收回．
|
|
一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1.
函数
的反函数是
A．y＝1－log2x (x＞0) B．y＝1＋log2x (x＞0)
C．y＝－1－log2x (x＞0) D．y＝－1＋log2x (x＞0)
2.
已知集合P＝{(x，y)｜y＝k}，Q＝{(x，y)｜y＝ax＋1}，且
，那么k的取值范围是
A．(－∞，1) B．(－∞，1] C．(1，＋∞) D．(－∞，＋∞)
3. (理科考生做)设复数z在映射f下的象为
，则－1＋2i的原象是
A．2－2i B．2－i C．－2 D．－1＋2 i
(文科考生做)已知z1＝1－2i，z2＝m
i，若
(m、n∈R)，则m的值为
A．1 B．
C．
D．－
4. 设直线3x＋4y－5＝0的倾斜角为
，则该直线关于直线x＝m(m∈R)对称的直线的倾斜角为
A．
B．
C．
D．
5. (理科考生做)下列不等式中有实数解的是
A．
≤0 B．
C．
≤
D．
(文科考生做)不等式｜x－1｜＞2x的解集是
A．{x｜x＜－1} B．{x｜x＜
}
C．{x｜－1＜x＜} D．{x｜x≠1，x∈R}
6. 长方体的全面积为72，则长方体的对角线长的最小值是
A．
B．
C．3 D．6
7. (理科考生做)若极坐标系的极点是直角坐标系的原点，极轴是x正半轴，直线l1的参数方程为
(t为参数)，直线l2的极坐标方程为
，则l1到l2的角为
A．
B．
C．
D．
(文科考生做) 直线l1在x轴上的截距3，在y轴上的截距为1，直线l2的方程为ax－y＋1＝0，直线l1到直线l2的角为45°，则a的值为
A． 
B． C．－2 D．－2或
8. 要使函数
在[1，2]上存在反函数，则a的取值范围是
A．a≤1 B．a≥2 C．a≤1或a≥2 D．1≤a≤2
9. 设函数
，若对任意x∈R都有f (x1)≤f (x)≤f (x2)成立，则 x1－x2 的最小值为
A．4 B．2 C．1 D．
10. 
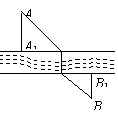在宽2公里的河两岸有A、B两个城市，它们的直线距离为10公里，A城到河岸的垂直距离AA1＝5公里，B城到河岸的垂直距离BB1＝1公里．现要选址建桥，使得从A到B的路程最短，则最短路程为
A．10公里 B．
公里
C．
公里 D．
公里
11. (理科考生做)已知两点M(－5，0)、N (5，0)，给出下列直线方程：①5x－3y＝0；②5x－3y－52＝0；③x－y－4＝0；④4x－3y＋15＝0．在直线上存在点P，满足 MP ＝ NP ＋6的所有直线方程是
A．②③ B．②④ C．①④ D．①②
(文科考生做)若双曲线
的左支上一点P (a，b)到直线y＝x的距离为
，则a＋b的值为
A．
B． C．－2 D．2
|
|
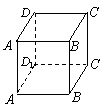
12. 
如图，在正方体A1B1C1D1－ABCD的侧面AB1内有一点P到棱AB与B1C1的距离相等，则动点P所在曲线的形状为(虚线部分)
A
B C
D
襄樊市高三年级统考试题(2003.4)
数 学
第 Ⅱ 卷 (非选择题，共90分)
注意事项：
第Ⅱ卷共6页，用黑色签字笔直接答在试题卷中，答卷前将密封线内的项目填写清楚．
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得 分 | |||||||||
| 得分 | 评卷人 |
二．填空题：本大题共4小题，每小题4分，共16分。将正确答案填在题中横线上．
13. 点A、B是抛物线
(p＞0) 上不同的两点，且OA＝OB(O是坐标原点)，若
△AOB的重心恰好是此抛物线的焦点，则直线AB的方程是 ．
14. 若函数
，则它的反函数f －1(x)＝ ．
15. 用1，2，3这三个数字组成一个四位数，要求这三个数字必须同时使用，且同一数字不能相邻出现，这样的四位数共有 (用数字作答)．
|
|
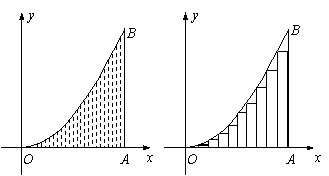
16. (理科考生做)抛物线
、x轴及直线AB：x＝a围成了如图(1)的阴影部分，AB与x轴交于A，把线段OA分成n等分，作以
为底的内接矩形如图(2)，阴影部分的面积S等于这些内接矩形面积之和当n→∞时的极限值，则S＝ ．
(文科考生做)已知数列{an}的通项
，Sn是其前n项和，则
＝ ．
可能使用的公式：
三．解答题：本大题共6小题，满分74分．
| 得分 | 评卷人 |
17. 
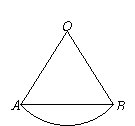
(本大题满分12分)
已知圆O的半径为1，圆心角∠AOB＝x(0＜x≤
)，弦AB的长记为y，函数f (x)＝y＋2
．
(理科考生做)求函数f (x)的单调区间．
(文科考生做)求函数f (x)的最大值和最小值，以及相应的x值．
| 得分 | 评卷人 |
|
|
18. (本大题满分12分)
在半径为1的圆中有一内接梯形PBAQ中，底边AB为圆的直径，以A、B为焦点的椭圆C过P、Q两点．
(1)当 PQ ＝1时，求椭圆C的方程；
(2)若直线PQ与椭圆C的右准线l相交于点M，求点M的轨迹方程．
19. (本大题满分12分)
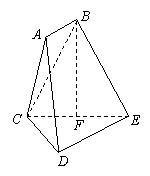
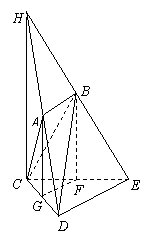
如图，在多面体ABCDE中，AB垂直平面ACD，DE垂直平面ACD，AC＝AD＝CD＝ED＝2，AB＝1，F为CE的中点．
(1)求证：直线BF⊥平面CDE；
(2)求多面体ABCDE的体积；
(3)求平面BCE与平面ACD所成二面角(锐角)的大小．
|
|
| 得分 | 评卷人 |
20. (本大题满分12分)
上因特网的费用由两部分组成：电话费和上网费．以前，××地区通过“××热线”上因特网的费用：电话费0.12元／3分钟，上网费0.12元／分钟．根据信息产业部调整因特网资费的要求，自1999年3月1日起，该地区上因特网的费用调整为：电话费0.16元／3分钟，上网费每月不超过60小时，以4.00元／小时计算，超过60小时的部分，以8.00／小时计算．
(1)根据调整后的规定，将每月上因特网的费用表示为上网时间(小时)的函数；
(2)某网民在调整前每月上网60小时的费用在调整后每月可上网多少小时？
(3) (理科考生做)从涨价和降价的角度分析该地区调整前、调整后上因特网的费用情况．
| 得分 | 评卷人 |
21. (本大题满分12分)
已知函数
(n∈N )，且a1，a2，a3，……，an构成一个数列{an}，满足
．
(1)求数列{an}的通项公式，并求
的值；
(2) (理科考生做)证明：0＜
＜1．
(文科考生做)若
，求数列{bn}的最大项和最小项．
| 得分 | 评卷人 |
22. (本大题满分14分)
(理科考生做)设函数
(a＞0且a≠1)，当点P (x，y)是函数y＝f (x)图象上的点时，点Q (x－2a，－y)是函数y＝g (x)图象上的点．
(1)写出函数y＝g (x) 的解析式；
(2)若当x∈[a＋2，a＋3]时，恒有 f (x)－g (x)
≤1，试确定a的取值范围．
| 得分 | 评卷人 |
(文科考生做) 设函数
(a＞0且a≠1)，当点P (x，y)是函数y＝f (x)图象上的点时，点Q (3x，
)是函数y＝g (x)图象上的点．
(1)写出函数y＝g (x) 的解析式；
(2)求不等式g (x)≤f (x)的解集．
数学参考答案及评分标准
一．选择题：ABBD(理(文 AACBB AC
二．填空题：13．x＝
14．
15．18 16．(理)
(文)
三．解答题：
17．解：在△AOB中，
3分
∵0＜x≤ ∴0＜
≤ 因此0＜
≤1
∴
5分
∴
7分
(理科)当
≤
≤
，即
≤x≤
时，f (x)单调递增
由于0＜x≤，∴f (x)的单调递增区间为 (0，
] 9分
当≤≤
，即≤x≤
时，f (x)单调递减
由于0＜x≤，∴f (x)的单调递减区间为 [，] 12分
(文科)∵0＜x≤，∴＜≤
，∴－2≤f (x)≤4 9分
∴函数f (x)的最大值为4，这时
，
f (x)的最小值为－2，这时
，
12分
18．(1)解：以BA所在直线为x轴，AB中点O为原点建立直角坐标系． 1分
当 PQ ＝1时，△OPQ为正三角形，边长为1，△OPA、△OQB也是边长为1的正三角形
∴ PA ＝1， PB ＝
∴
3分
又c＝1，∴
故所求轨迹方程为：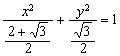
5分
(2)解：设椭圆C的方程为
(m＞n＞0)，则其右准线方程为x＝m2
设M(x，y)，P(x0，y0)
由于△APB是直角三角形，∴ PA 2＋ PB 2＝ AB 2＝4
故( PA ＋ PB )2－2 PA PB ＝4，即4m2－2 PA PB ＝4 6分
又 PA PB ＝ AB y0 ，∴4m2－4 y0 ＝4
∴y0＝±(m2－1) 8分
由
得：y＝±(x－1) 10分
∵0＜ y0 ＜1，∴0＜m2－1＜1 Þ 1＜m2＜2m Þ 1＜x＜2
∴点M的轨迹方程是y＝±(x－1) (1＜x＜2)． 12分
|
|
19．(1)证法一：取CD中点G，连AG和FG，则AG⊥CD，GF∥DE，GF＝DE＝1
∵DE⊥平面ACD，∴平面ACD⊥平面CDE
故AG⊥平面CDE
∵AB⊥平面ACD，DE⊥平面ACD
∴AB∥DE，AB＝DE
∴AGFB是平行四边形 Þ AG∥BF
而AG⊥平面CDE
∴BF⊥平面CDE 4分
证法二：∵AB⊥平面ACD，∴AB⊥AC，AB⊥AD
在Rt△BAD中，
又DE⊥平面ACD，∴DE⊥AD
∴ADEB是直角梯形，∴
又F为CE的中点，∴BF⊥CE
在Rt△CDE中，
，∴
在Rt△BFE中，
在Rt△BAD中
∵BF 2＋DE 2＝5＝BD 2，∴BF⊥DF
因此BF⊥平面CDE． 4分
(2)解：连结BD，则
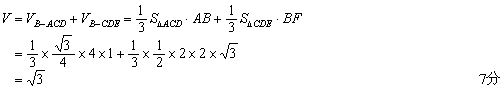
(3)解：延长EB和DA交于H，连HC，则HC是所求二面角的棱
∵AB∥DE，AB＝DE，∴B是HE的中点
又F是CE的中点，∴BF∥HC
因此HC⊥平面CDE，故HC⊥CD，HC⊥CE
∴∠ECD为所求二面角的平面角
由于∠ECD＝45°，∴平面BCE与平面ACD所成二面角为45°． 12分
20．(1)解：设调整后上网时间为t (小时)，费用为y(元)，则由题意，得
即
(理)5分(文)6分
(2)解：调整前60小时的费用总支出为(0.12×20＋0.12×60)×60＝576元
调整后若使用60小时，则费用y＝7.2×60＝432元
∴576＝11.2t－240，解得：t＝72.85小时
∴调整前每月上网60小时的费用在调整后每月可上网72.85小时． (理)10分(文)12分
(3)解：调整前每小时总费用为0.12×20＋0.12×60＝9.6元
∴调整前总费用与时间t(小时)的关系为y＝9.6t
令11.2t－240＝9.6t，解得t＝150小时．
当一网民每月上网时间t＝150小时，前后支出相同；
当一网民每月上网时间t＜150小时，调整后支出少，属降价；
当一网民每月上网时间t＞150小时，调整后支出多，属涨价． 12分
21．(1)解：∵f (1)＝a1＋a2＋a3＋……an＝n2，∴数列{an}的前n项和Sn＝n2
∴an＝Sn－Sn－1＝n2－(n－1)2＝2n－1(n≥2)
又a1＝S1＝1，满足an＝2n－1
∴数列{an}的通项公式为an＝2n－1(n∈N)
(2) (理科)证法一：∵
两式相减得：
∴
∵
(n∈N)
∴0＜
＜1，∴0＜1－＜1，即0＜＜1．
证法二：……
显然＜1，下面证明＜1
当n＝1时，
＜1，结论成立
假设当n＝k时结论成立，即＜1，则n＝k＋1时
∴n＝k＋1时，结论成立
因此＜1对一切自然数成立
∴＞0．
(文科)
当2n－21＞0，即n≥11时，bn随n的增大而减小
∴b11＞b12＞b13＞……＞2 ①
当2n－21＜0，即n≤10时，bn随n的增大而减小
∴2＞b1＞b2＞……＞b10 ②
由①②得：b11＞b12＞b13＞……＞2＞b1＞b2＞……＞b10
∴数列{an}的最大项为b11＝3，最小项为b10＝1．
22．(理科)(1)解：设点Q的坐标为(x0，y0)，则x0＝x－2a，y0＝－y，即x＝x0＋2a，y＝－y0
∵点P (x，y)在函数
的图象上，
∴
，即
∴
． 4分
(2)解：由题意(a＋2)－3a＝－2a＋2＞0，
又a＞0且a≠1，∴0＜a＜1 ① 5分
∵ f (x)－g (x)
≤1，∴－1≤
≤1
∵0＜a＜1，∴a＋2＞2a，r(x)＝x2－4ax＋3a2在[a＋2，a＋3]上是增函数
函数
在[a＋2，a＋3]上是减函数 7分
从而
因此所求问题转化为求不等式组
的解． 10分
由loga(9－6a)≥－1得：0＜a≤
②
由loga(4－4a)≤1得：0＜a≤
③
由①②③得所求a的取值范围是0＜a≤． 14分
(文科)(1)解：解：设点Q的坐标为(x0，y0)，则x0＝3x，y0＝，即x＝x0，y＝2y0
∵点P (x，y)在函数
的图象上，
∴
，即
∴
． 5分
(2)解：不等式即为
≤loga (x－1)
当a＞1时，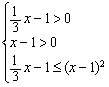
，解得：x＞3 8分
当0＜a＜1时，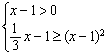
，无解 12分
∴当a＞1时，不等式g(x)≤f (x)的解集是{x｜x＞3}；当0＜a＜1时，不等式g(x)≤f (x)的解集为φ． 14分