试卷类型：A
襄樊市高三年级统考试题
数 学(文史类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分，考试用时120分钟．
第 Ⅰ 卷 (选择题，共60分)
注意事项：
1．请考生将自己的学校、班级、姓名、学号填写在第Ⅱ卷密封线内．
2．每小题选出答案后用2B铅笔把答题卡上对应题目的答案代号涂黑，如需改动，必须用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．
3．考试结束后，监考人员将本试卷和答题卡一并收回．
参考公式：
|
|
一．选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1. m＝－2是直线(2－m)x＋my＋3＝0和直线x－my－3＝0互相垂直的
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分又不必要条件
2. 若指数函数y＝f (x)的反函数的图象经过点(2，－1)，则此指数函数是
A．
B．
C．
D．
3. 把直线x－2y＋k＝0沿向量a＝(－1，－2)平移后，所得直线正好与圆x2＋y2＋2x－4y＝0相切，则实数k的值为
A．3或13 B．－3或13 C．3或－13 D．－3或－13
4. 若椭圆
(a＞b＞0)的离心率为
，则双曲线
的离心率为
A．
B．
C．
D．
5. 不等式
＜2的解集是
A．(
，－1)∪(1，
) B．(－∞，)∪(，+∞)
C．(－∞，1)∪(，+∞) D．(－，1)∪(，+∞)
6. 函数f (x)＝ log a x (0＜a＜1)的单调递减区间是
A．(0，a] B．(0，+∞) C．(0，1] D．[1，+∞)
7. 曲线
在点(
)处切线的倾斜角为
A．30° B．45° C．135° D．150°
8. 关于x的方程
有一个根为1，则△ABC中一定有
A．A＝B B．A＝C C．B＝C D．A＋B＝
9. 在边长为1的菱形ABCD中，∠ABC＝60°，将菱形沿对角线AC折起，使折起后BD＝1，则二面角B—AC—D的大小为
A．
B．
C．
D．
10. 若函数
对任意的实数都有
，则
＝
A．0 B．1 C．－1 D．1或－1
11. 从集合｛1，2，3，…，10｝中任意选出三个不同的数，使这三个数成等比数列，这样的等比数列个数为
A．3 B．4 C．6 D．8
12. 
一个正整数数表如下(表中下一行中的数的个数是上一行中数的个数的2倍)：
则第8行中的第5个数是
A．68 B．132 C．133 D．260
襄樊市高三年级调研测试题(2004.3)
数 学(文史类)
第 Ⅱ 卷 (非选择题，共90分)
注意事项：
第Ⅱ卷共6页，用黑色签字笔直接答在试题卷中，答卷前将密封线内的项目填写清楚．
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得 分 | |||||||||
| 得分 | 评卷人 |
二．填空题：本大题共4小题，每小题4分，共16分。将正确答案填在题中横线上．
13. 等比数列{an}中，Tn表示前n项的积，若T5＝1，则a3＝ ．
14.
已知x、y满足：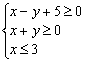
，则z＝x＋2y的最大值是 .
15. 某地区普通高中分为三类，A类学校共有学生4000人，B类学校共有学生2000人，C类学校共有学生3000人，现欲抽样分析某次考试的成绩，若抽取900份试卷进行分析，则从A类学校抽取的试卷份数应为 ．
16.
已知(4－a)n (3＋a)n 的展开式中各项系数之和为an ，(1＋5x)n的展开式中各项系数之和为bn ，则
的值是
．
三．解答题：本大题共6小题，满分74分．
| 得分 | 评卷人 |
17.
(本大题满分12分)已知向量a＝(cosx，sinx)，b＝(
)，且x∈[0，]．求函数f (x)＝a · b－｜a＋b｜的最小
值．
| 得分 | 评卷人 |
18.
(本大题满分12分)在袋里装30个小球，其中彩球中有2个红色、5个蓝色、10个黄色，其余为白球．求：
(1)从袋里取出3个都是相同颜色彩球(无白色)的概率；
(2)从袋中任取3个小球至少有一个是红球的概率．
19.
(本大题满分12分) 已知等比数列{xn}的各项为正数，数列{yn}满足
(a＞0且a≠1)，设y3＝18，y6＝12．
(1)求数列{yn}的前多少项和最大，最大值为多少？
(2)是否存在自然数M，使当n＞M时，xn＞1恒成立？，若存在，求出M的最小值；若不存在，说明理由．
| 得分 | 评卷人 |
20.
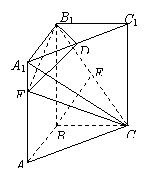
(本大题满分12分)在直三棱柱ABC－A1B1C1中，底面△ABC是等腰直角三角形，∠ABC＝90°，AC＝2a，AA1＝3a，D、E分别为A1C1、B1C的中点，点F在AA1上，且AF＝2a．
(1)求异面直线A1C和BE所成的角
；
(2)求证：CF⊥平面B1DF．
| 得分 | 评卷人 |
|
|
21.
(本大题满分12分) 直线l：y＝x＋1与曲线C：x2＋ay2＝1相交于P、Q两点．
(1)当实数a为何值时，
；
(2)是否存在实数a，使得OP⊥OQ (O是坐标原点)？若存在，求出a的值；若不存在，说明理由．
| 得分 | 评卷人 |
22.
(本大题满分14分) 已知a＞0，函数
，x∈[0，+∞)，设x1＞0，记曲线y＝f (x)在点M (x1，f (x1))处的切线为l．
(1)求l的方程；
(2)设l与x轴交点为(x2，0)，证明：①x2≥
②若
，则
．
| 得分 | 评卷人 |
数学参考答案及评分标准(文史类)
说明：
1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．
2．对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．
3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．
4．只给整数分数，选择题和填空题不给中间分数．
一．选择题：AAABB CBABD DC
二．填空题：13．1 14．19 15．400 16．
三．解答题：
17．解：解：a · b
2分
a＋b 
4分
∴cos x≥0，因此 a＋b ＝2 cos x
6分
∴0≤cos x≤1
∴当且仅当
取得最小值
． 12分
18．(1)解：取3个球的方法数为
2分
设“3个球全红色”为事件A，“3个全蓝色”为事件B，“3个球全黄色”为事件C，则
，
，
4分
∵A、B、C为互斥事件
∴P(A＋B＋C)= P(A)＋P(B)＋P(C)
8分
(2)解：记“3个球中至少有一个是红球”为事件D，则
为“3个球中没有红球”
12分
19．(1)解：设{xn}的公比为q(q≠1)
∵
∴{yn}为等差数列，设公差为d 2分
∵y3＝18，y6＝12，∴d＝－2
∴yn＝y3＋(n－3)(－2)＝24－2n 4分
设前k项和为最大，则
∴前11项和与前12项和为最大，且最大值为132 6分
(2)解：由(1)得：2logaxn＝24－2n ，∴xn＝a12－n，n∈N* 8分
若xn＞1，则a12－n＞1
当a＞1时，n＜12，显然不存在满足条件自然数M 10分
当0＜a＜1时，n＞12，
∴存在M＝12，13，14，…，使当n＞M时，xn＞1恒成立，且M的最小值为12 12分
|
|
20．方法一：
(1)解：以
为x轴、y轴、z轴建立空间直角坐标系
∵AC＝2a，∠ABC＝90°
∴AB＝BC＝
从而A (，0，0)，C (0，，0)，A1(，0，3a)，B1(0，0，3a)，C1(0，，3a) 2分
∴D(
)，E(
)
∴
，
4分
因此
∴
6分
(2)证：F(，0，2a)，
，
，
8分
∵
10分
∴CF⊥B1D，CF⊥B1F
∴CF⊥平面B1DF． 12分
方法二：
(1)解：取A1B1中点G，连EG，则EG∥A1C，连BG
则GE与BE所成的角即为异面直线A1C和BE所成的角
2分
在△BEG中，GE
，
4分
∴
∴
6分
(2)证：∵D是A1C1中点，∴B1D⊥A1C1 ，故B1D⊥平面A1ACC1
因此B1D⊥CF
8分
在Rt△B1FC中，
，
在Rt△AFC中，
在 Rt△BB1C中，
10分
∵B1F2+FC2=B1C2，∴CF⊥FB1
∴CF⊥平面B1DF 12分
21．(1)解：由
得： (1＋a)x2＋2ax＋(a－1)＝0 ①
若1＋a＝0，则直线l与双曲线C的渐近线平行，故l与C只可能有一个交点，不合题意
∴1＋a≠0 2分
设P(x1，y1)，Q(x2，y2)，则
，且△＝4a2－4(a－1)(a＋1) ＝4＞0
4分
若 ，则
，解得：a＝或a＝3
∴当a＝或a＝3 时， 6分
(2)解：
若存在实数a，使
，则
Û x1x2＋y1y2＝0 8分
即x1x2＋(x1＋1)(x2＋1)＝0 Û 2x1x2＋(x1＋x2)＋1＝0
∴
＝0，解得：a＝1
∴存在实数a＝1，使得 12分
22．(1)解：
，∴曲线y＝f (x)在点M (x1，f (x1))处的切线的斜率
∴切线l的方程为
，即
4分
(2)解：令y＝0得
①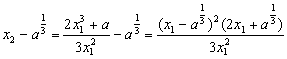
≥0 (*) 8分
∴
，当且仅当
时等号成立． 10分
②∵，∴(*)中“＝”不成立，故
12分
∵
∴
，故x2＜x1
∴当时，成立． 14分