北京市海淀区高三数学（文科）第二学期期中练习参考答案与评分标准
2001.5
一、选择题：
（1）C； （2）D； （3）B； （4）C； （5）A； （6）B；
（7）C； （8）C； （9）B； （10）C； （11）D； （12）D.
二、填空题：
（13）12；
（14）
（15）
； （16）
（写出一个即可）
三、解答题：
（17）解（I）：设z=a+bi (a,
) ∴
………………………………1分
由已知，有
，可解出
或
∴
或
………………………………………………………………………3分
∴
，
………………………………………………………………………5分
∴
或
……………………………………7分
（Ⅱ）：当
时，可得
，
∴A（1，1），B（0，2），C（1，–1）
∴
………………………………………………………………………10分
∴当
时，可得，
∴A（–1，–1），B（0，2），C（–1，–3）
∴
综上
的面积为1.………………………………………………………………………12分
|
是正三角形，AF是BC边中线，
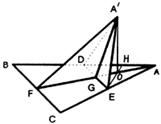
∴AF⊥BC.
∵D、E分别是AB、AC的中点，
∴DE∥BC， ∴AF⊥DE.
又AF∩DE=G，
∴
⊥DE，FG⊥DE，又∩FG=G，
∴DE⊥平面
.……………………4分
又DE
平面DECB，
∴平面⊥平面DECB.…………6分
（Ⅱ）解：∵⊥DE，GF⊥DE，
∴∠
是二面角
的平面角.
………………………………………7分
∵平面⊥平面BCED，作
⊥AG于O，
∴⊥平面BCED.
设
,连结EO并延长交AD于H，
∴EH⊥AD.
∵AG⊥DE,.
∴O是正三角形ADE的垂心也是中心.
∵AD=DE=AE=
,
∴
,
.
在
中,
.
∵
,
∴
.
即当
的余弦值为
时,
与BD互相垂直.…………………12分
（19）解（I）：∵当
时，
，
，
成等差数列，
∴
，………………………………………………1分
∴
（）.
由
,可得
，∴
.………………………………2分
同理，可求出
，
.…………………………………………4分
（Ⅱ）：当时，∵
①，
∴
②，
②–①得
.
∴
为常数，……………………………………………………6分
∴
，
，
，…，，…成等比数列，其中首项，
.…
…………………………………………………………………………7分
∴通项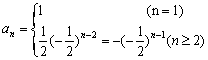
.……9分
（Ⅲ）：∵
∴
=
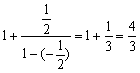…………………………………………12分
（20）解（I）：∵
是以5为周期的周期函数，
∴
.
∵函数 (
)是奇函数，
∴
.
∴
.……………………………………………………………6分
（Ⅱ）：当
时，由题意，可设
（
），
由，得
，
∴
.
∴
(
). ……………………………………12分
（21）解（I）：由已知数据，易知
的周期T=12，
………………………………1分
∴
.
由已知，振幅A=3，b=10，………………………………………………………3分
∴
.…………………………………………………………………4分
（Ⅱ）：由题意，该船进出港时，水深应不小于
（米），
∴
.………………………………………………………………6分
即
.
解得，
（
），
∴
（） .………………………………………………8分
在同一天内，取
或1，∴
或
. …………………………10分
答：该船可在当日凌晨1时进港，17时离港，它在港内至多停留16小时 。
………………………………………………………………………………………12分
（22）解（I）：∵
，又圆D与圆C外切（O为原点），
∴圆D半径
.……………………………………………………2分
此时，A、B坐标分别为（0，0），（0，6）.
又PA在x轴上,PB斜率k=2，
∴
.………………………………………………………………5分
（Ⅱ）：设D点坐标为（0，a），圆D的半径为r，则
①……6分
∴A、B两点坐标为
，
.
设PA、PB的斜率分别为
、
，
∴
，
.………………………………………………8分
∴
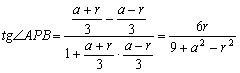②
由①得
代入②，得
.
而
为单调增函数……………………………………………………10分
由圆D与圆C外切,知
，………………………………………12分
∴
取值范围是
即的最大值是
.………………………………………………14分
注：其它正确解法可按相应步骤给分.