黄冈中学鄂南高中2006届高三年级联合月考
数学试题(文)
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中只有一项符合题目要求,将正确选项的字母填在答题栏相应的表格中。)
1、设集合![]() ,则
,则![]() 中元素的个数有
中元素的个数有
A.2个 B.3个 C.4个 D.无数个
2、在实数等比数列![]() 中,
中,![]() ,则
,则![]()
A.8 B.8 C.![]() D.
D.![]()
3、函数![]() 图象的对称中心的坐标不能是
图象的对称中心的坐标不能是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、函数![]() ,给出下列四个命题:
,给出下列四个命题:
①函数![]() 在区间
在区间![]() 上是减函数;
上是减函数;
②直线![]() 是函数
是函数![]() 的图象的一条对称;
的图象的一条对称;
③函数![]() 的图象可以由函数
的图象可以由函数![]() 的图象向左平移
的图象向左平移![]() 而得到。
而得到。
A.①③ B.①② C.②③ D.①②③
5、关于![]() 的方程
的方程![]() 有负根,则
有负根,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、已知函数![]() 在区间
在区间![]() 上至少取得2个最大值,则正整数t的最小值是
上至少取得2个最大值,则正整数t的最小值是
A.9 B.10 C.11 D.12
7、 已知O为![]() 所在平面内一点,且满足
所在平面内一点,且满足![]() ,则O是
,则O是![]() 的
的
A.重心 B.外心 C.垂心 D.内心
8、若![]() ,则函数
,则函数![]() 的最小值是
的最小值是
A.![]() B.0 C.2 D.4
B.0 C.2 D.4
9、若函数![]() 是定义在
是定义在![]() 上的增函数,且对一切
上的增函数,且对一切![]() 满足
满足![]() ,则不等式
,则不等式![]() 的解集为
的解集为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、已知函数![]() 的定义域为R,它的反函数为
的定义域为R,它的反函数为![]() ,且满足
,且满足![]() ,则
,则![]() 的值为
的值为
A.![]() B.0 C.-1 D.-2
B.0 C.-1 D.-2
11、![]() 中,a、b、c分别为角A、B、C的对边,如果
中,a、b、c分别为角A、B、C的对边,如果![]() 成等比数列,
成等比数列,![]() 那么
那么![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12、在![]() 中,
中,![]() 设
设![]() ,则
,则![]()
A.4 B.5 C.6 D.7
二、填空题(本大题共4小题,每小题4分,共16分。将答案写在答题栏相应位置。)
13、在数列中,已知![]() ,这个数列的通项公式是
。
,这个数列的通项公式是
。
14、设![]() 且满足
且满足![]() ,则xy的最大值是
。
,则xy的最大值是
。
15、已知直角坐标系内有三个定点![]() ,若动点P满足:
,若动点P满足:![]() ,则点P的轨迹方程
。
,则点P的轨迹方程
。
16、有一台天平,两臂长略有差异,其他均精确,现将一物体A放在左右托盘内各称一次,称得结果分别为![]() 克和
克和![]() 克
克![]() ,关于物体A的重量,有下列说法:
,关于物体A的重量,有下列说法:
①物体A的重量是![]() 克;②物体A的重量介于
克;②物体A的重量介于![]() 克与
克与![]() 克之间;③物体A的重量大于
克之间;③物体A的重量大于![]() 克
克![]() ;④物体A的重量大于
;④物体A的重量大于![]() 克;
克;
其中所有正确的说法序号有: 。
三、解答题(本大题共6小题,共74分。解答应写出文字说明、证明过程和演算步骤)
17、(本题满分12分)设全集![]() 函数
函数![]() 的定义域为A.,集合
的定义域为A.,集合![]() , 若
, 若![]() 恰有2个元素,求a的取值集合。
恰有2个元素,求a的取值集合。
18、(本题满分12分)已知关于x 的不等式 ![]() 和
和 ![]() 的解集分别为A和B,且
的解集分别为A和B,且![]()
求实数![]() 的取值集合。
的取值集合。
19、(本题满分12分)已知平面向量![]() ,
, ![]() ,
, ![]() 若
若![]() ,求角
,求角![]()
20、(本题满分12分)已知函数![]() ,
,![]()
![]() 时f(x)的值域里的元素的整数的个数记为
时f(x)的值域里的元素的整数的个数记为![]() ,设
,设![]()
(Ⅰ)设![]()
![]() ,求
,求![]() ;
;
(Ⅱ)设数列![]() 的前
的前![]() 项之和为
项之和为![]() , 记
, 记 ![]() O为平面直角坐标系原点),求证:对任意
O为平面直角坐标系原点),求证:对任意![]() ,向量
,向量![]() 都共线。
都共线。
21、(本题满分14分)已知定点A(1,0)和直线![]() 上的两个动点E、F且
上的两个动点E、F且![]() ,动点
,动点![]() 满足
满足![]() (其中O为坐标原点)。
(其中O为坐标原点)。
(Ⅰ)求动点![]() 的轨迹C的方程;
的轨迹C的方程;
(Ⅱ)过点B(0,2)的直线![]() 与(Ⅰ)中轨迹C相交于两个不同的点M、N,若
与(Ⅰ)中轨迹C相交于两个不同的点M、N,若![]() ,求直线
,求直线![]() 的斜率的取值范围。
的斜率的取值范围。
22、(本题满分12分)已知实数a,b,c满足:![]()
(1)求证:a>0,c<0;
(2)
求证:![]()
(3)设抛物线![]() 被X轴截得的弦长为
被X轴截得的弦长为![]()
![]() ,求
,求![]() 的取值范围
的取值范围
数学(文)参考答案
一、选择题:DABA,CCDD,BCCB
二、填空题
13.![]() 14﹒1 15﹒
14﹒1 15﹒![]() 16﹒②④
16﹒②④
三、解答题
17.解:依题意得![]() ①
①
当![]() 时,
时,![]() ①
①![]() 或
或![]()
即![]() 或
或![]()
![]()
![]() (4分)
(4分)
![]()
![]()
![]() (8分)
(8分)
当![]() 时,
时,![]() 在此区间上恰有2个偶数
在此区间上恰有2个偶数
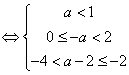 解得
解得![]()
所以![]() 的取值集合为
的取值集合为![]() .
.
![]() (12分)
(12分)
18.解: ![]() 或
或![]() 或
或![]()
![]() 或
或![]() ①
①
![]() (5分)
(5分)
又![]()
![]() ②
②
![]() (10分)
(10分)
由①②知![]() ,即
,即![]() 的取值集合为
的取值集合为![]()
19.解:由题意知![]()
![]() (2分)
(2分)
![]()
![]() (4分)
(4分)
即![]()
![]()
![]() (6分)
(6分)
![]()
![]()
![]() (8分)
(8分)
![]() 所以
所以![]() 故
故![]()
![]() (10分)
(10分)
![]() 即
即![]() .
.
![]() (12分)
(12分)
20.(Ⅰ)易知![]()
![]() (2分)
(2分)
![]()
![]() 则数列
则数列![]() 是公差为
是公差为![]() 的等差数列
的等差数列![]() (4分)
(4分)
![]()
![]()
![]() (6分)
(6分)
(II)![]()
![]() (8分)
(8分)
![]() 向量
向量![]()
![]() (10分)
(10分)
即向量![]() 与向量
与向量![]() 共线,所以对任意
共线,所以对任意![]() 、
、![]() ,向量
,向量![]() 都共线。
都共线。
![]() (12分)
(12分)
21.(I)设![]() (
(![]() 、
、![]() 均不为)
均不为)
由![]() //
//![]() 得
得![]() ,即
,即![]()
![]() (2分)
(2分)
由![]() //
//![]() 得
得![]() ,即
,即![]()
![]() (4分)
(4分)
由![]() 得
得![]()
![]() 动点
动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]()
![]() (6分)
(6分)
(II)设直线![]() 的方程为
的方程为![]()
联立![]() 消去
消去![]() 得
得![]()
![]() ,
,
![]() (8分)
(8分)
且![]() 即
即![]() ①
①
![]() (9分)
(9分)
![]()
![]()
![]()
![]() (12分)
(12分)
![]() ②
②
综合①②知直线![]() 的斜率的取值范围为
的斜率的取值范围为![]()
![]() (14分)
(14分)
22.解:(I)若![]() ,则
,则![]() 故
故![]() ,与题意矛盾,故
,与题意矛盾,故![]()
![]() (2分)同理可证C<0所以a>0,c<0
(2分)同理可证C<0所以a>0,c<0
(II)![]() 中得
中得
![]()
![]() (6分)
(6分)
(III)高抛物线与![]() 轴的两个交点横坐标为
轴的两个交点横坐标为![]() ,则
,则![]() 、
、![]() 为应方程
为应方程![]() 的两个根,
的两个根,
![]()
![]() (8分)
(8分)
![]()
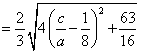
![]() (10分)
(10分)
![]() ,即
,即![]() 的取值范围为
的取值范围为![]()
![]()
![]() (12分)
(12分)