临沭县实验中学高三数学(文)模拟试题(二)
一、选择题:本大题共12小题.每小题5分;共60分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.已知集合![]() Z},则集合
Z},则集合![]() ,则集合
,则集合![]() ∩B等于
∩B等于
A.{0, 2} B.{ 0,1 } C.{1, 2} D.{ 0 }
2.给出下列命题:①![]() ,则
,则![]() 或
或![]() ②若
②若![]() 为单位向量且
为单位向量且![]() ,则
,则![]() ③若
③若![]() 且
且![]() ,则
,则![]() ④若
④若![]() 与
与![]() 共线,
共线,![]() 与
与![]() 共线,则
共线,则![]() 与
与![]() 共线。 其中正确命题的个数是
共线。 其中正确命题的个数是
A. 0 B. 1 C. 2 D. 3
3.已知函数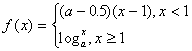 在
在![]() 内是减函数,则a的取值范围是
内是减函数,则a的取值范围是
A. (0,1) B.
(0,0.5)
C. (![]() ,0.5) D.
(0.5,1)
,0.5) D.
(0.5,1)
4.不等式![]() 成立的一个必要非充分条件是
成立的一个必要非充分条件是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.三棱锥P-ABC的三个侧面两两垂直,PA=12 ,PB=16 ,PC=20,若P、A、B、C四点都在同一个球面上,则此球面上A、B两点间的球面距离为
A.![]() B.
B.![]() C.10 D.
C.10 D.![]()
6.设![]() 是两条不同直线,
是两条不同直线,![]() 是两个平同的平面,则下列四个命题:①若
是两个平同的平面,则下列四个命题:①若![]() ,则
,则![]() ∥
∥![]() ;②若a∥
;②若a∥![]() ,
,![]() ,则
,则![]() ;③若
;③若![]() ,
,![]() ,则
,则![]() ∥
∥![]() ;④若
;④若![]() ,则
,则![]() .则其中正确命题的序号是
.则其中正确命题的序号是
A.① B.② C.③ D.④
7.设双曲线![]() 的一条准线方程为
的一条准线方程为![]() ,则k的值为
,则k的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.将函数![]() 的图像按向量
的图像按向量![]() 平移后,所得图像解析式
平移后,所得图像解析式
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
9.已知函数![]() 在区间
在区间![]() 上是增函数,则实数
上是增函数,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]()
C.![]() ∪
∪![]() D.
D.![]()
10.已知等比数列![]() ,则使不等式
,则使不等式![]()
成立的最大自然数![]() 是
是
A.4 B.5 C.6 D.7
 11.将3种农作物都种植在如图的4块试验田里,
11.将3种农作物都种植在如图的4块试验田里,
每块种植一种农作物,要求相邻的试验田不能
种植同一种作物,则不同的种植方法共有
A.6种 B.12种 C.18种 D.24种
12. 定义在(![]() ,0)
,0)![]() (0,
(0,![]() )上的奇函数
)上的奇函数![]() ,在(0,
,在(0,![]() )上为增函数,当x>0时,
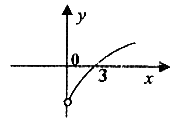
)上为增函数,当x>0时,![]() 图像如图所示,则不等式
图像如图所示,则不等式![]() 的解集为
的解集为
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
二、填空题:本大题共6小题,每小题4分,共24分.把答案填在题中横线上.
13.若![]() (
(![]() 是常数,且
是常数,且![]() )的展开式中常数项为70,则此展开式中各项系数的
)的展开式中常数项为70,则此展开式中各项系数的
和是 .
14.已知圆C的方程为![]() ,若
,若![]() ,
,![]() 两点一个在圆C的内部,一个在圆C的外部,则实数a的取值范围是 .
两点一个在圆C的内部,一个在圆C的外部,则实数a的取值范围是 .
15.在正方体![]() 中,
中,![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 在线段
在线段![]() 上运动,异面直线
上运动,异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,则
,则![]() 的取值范围是
.
的取值范围是
.
16.已知![]() ∥
∥![]() ,O 为坐标原点,当t变化时,则点 P的轨迹方程为
,O 为坐标原点,当t变化时,则点 P的轨迹方程为
临沭县实验中学高三数学(文)模拟试题(二)
三. 解答题(本大题共6个小题,满分74分。解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
某企业生产的产品有一等品和二等品两种,按每箱10件进行包装,每箱产品均需质检合格后方可出厂.质检办法规定:从每箱产品中任抽4件进行检验,若二等品不超过1件,就认为该箱产品合格;否则,就认为该箱产品不合格.已知某箱产品中有2件二等品.
(1)求该箱产品被某质检员检验为合格的概率;
(2)若甲、乙两质检员分别对该箱产品进行质检,求甲、乙两人得出的质检结论不一致的概率.
18.(本题满分12分)
设函数![]() ,其中向量
,其中向量![]() ,
,![]() ,
,![]()
(1)求![]() 的最小正周期; (2)在
的最小正周期; (2)在![]() 中,a,b,c分别是角A,B,C的对边,
中,a,b,c分别是角A,B,C的对边,![]() ,
,![]() ,
,![]() ,求b,c的长
,求b,c的长
19.(本题满分12分)
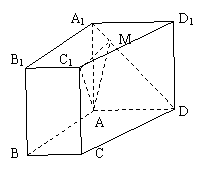 如图,直四棱柱
如图,直四棱柱![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,异面直线
,异面直线![]() 与
与![]() 互相垂直。
互相垂直。
(1)求直棱柱棱![]() 的长;
的长;
(2)若点![]() 在线段
在线段![]() 上,
上,![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角的大小。
所成的角的大小。
20.(本题满分12分)
已知函数![]()
(1)求证:函数![]() 在(0,
在(0,![]() )上是增函数;
)上是增函数;
(2)若![]() 在[1,
在[1,![]() )上恒成立,求实数a的取值范围;
)上恒成立,求实数a的取值范围;
(3)若函数![]() 在
在![]() 上的值域是
上的值域是![]() ,求实数a的取值范围。
,求实数a的取值范围。
21.(本题满分13分)
已知![]() (c>0),
(c>0),![]() (n, n)(n∈R),
(n, n)(n∈R), ![]() 的最小值为1,若动点P同时满足下列三个条件:①
的最小值为1,若动点P同时满足下列三个条件:①![]() ,②
,②![]() (其中
(其中![]() );③动点P的轨迹C经过点B(0,-1)。 (1)求c值; (2)求曲线C的方程;
);③动点P的轨迹C经过点B(0,-1)。 (1)求c值; (2)求曲线C的方程;
(3)方向向量为![]() 的直线l与曲线C交于不同两点M、N,若
的直线l与曲线C交于不同两点M、N,若![]() ,求k的取值范围。
,求k的取值范围。
22.(本题满分13分)
已知二次函数![]() 经过点(0,10),其导数
经过点(0,10),其导数![]() ,当
,当![]() (
(![]() )时,
)时,![]() 是整数的个数记为
是整数的个数记为![]() 。
。
(1)求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,求数列
,求数列![]() 的前n项(
的前n项(![]() )项和
)项和![]() 。
。
临沭县实验中学高三数学(文)模拟试题(二)参考答案
一. 选择题 : 1.A 2.A 3.B 4.C 5.A 6.D 7.B 8.A 9.A 10.B 11.C 12.A
二.填空题: 13 . 0 14 . ![]() 15 .
15 . ![]() 16 .
16 . ![]()
三. 解答题
17.解:(1)从一箱产品中抽出4件,可能出现的结果数为![]() .由于是任意抽取,这些结果出现的可能性都相等.因该箱产品中有2件二等品,故取到的二等品不超过1件的结果数为
.由于是任意抽取,这些结果出现的可能性都相等.因该箱产品中有2件二等品,故取到的二等品不超过1件的结果数为![]() .记“该箱产品被某质检员检验为合格”为事件A,那么事件A的
.记“该箱产品被某质检员检验为合格”为事件A,那么事件A的
概率为![]()
![]() ………………………………………………… 4分
………………………………………………… 4分
答:该箱产品被某质检员检验为合格的概率为![]() . ……………………………… 6分
. ……………………………… 6分
(2)记“甲、乙两质检员分别对该箱产品进行质检,甲的质检结论为合格”为B, “甲、乙两质检员分别对该箱产品进行质检,乙的质检结论为合格”为C.“甲、乙两人得出的质检结论不一致”包括两种情况:一种是甲的质检结论为合格,但乙的质检结论不合格;另一种是乙的质检结论合格,但甲的质检结论不合格.故所求的概率为
![]() .
.
答:甲、乙两人得出的质检结论不一致的概率为![]() .……………………………12分
.……………………………12分
18.解:(1)![]()
![]() …………………………4分
…………………………4分
![]() 的最小正周期为
的最小正周期为![]() . …………………………6分
. …………………………6分
(2) 由 ![]() 得
得![]() ,
,![]()
![]() 为三角形的内角 ,
为三角形的内角 ,![]() …………………………8分
…………………………8分
由![]() 得
得![]()
![]() 则
则 ![]() , 解得:
, 解得: ![]() 或
或![]() , ………………11分
, ………………11分
![]()
![]() …………………………12分
…………………………12分
19.解:(1)方法1: 以A为坐标原点以AB、AD、AA1所在直线分别x轴、y轴、Z轴建立直角坐标系,设棱![]() 的长为
的长为![]() C(5,2,0),D(0,8,0),A1(0,0,a), B1(5,0,a), C1(5,2,a),D1(0,8,a).∴
C(5,2,0),D(0,8,0),A1(0,0,a), B1(5,0,a), C1(5,2,a),D1(0,8,a).∴![]()
![]() ,——3分
,——3分
又![]() , 得
, 得![]() ,∴棱
,∴棱![]() 的长为4。——8分
的长为4。——8分
方法2 、设棱![]() 的长为
的长为![]() 在A1D1
上取点E1,使A1E1=2,则点E1即为点C1在平面AA1D1D上的射影,AE1⊥A1D。连C1E、AE1,易知A1D⊥平面AC1E1,
在A1D1
上取点E1,使A1E1=2,则点E1即为点C1在平面AA1D1D上的射影,AE1⊥A1D。连C1E、AE1,易知A1D⊥平面AC1E1,
在平面AA1D1D中,由Rt△AA1D~Rt△AA1E
∴![]() ,即
,即![]() 。∴
。∴![]() ∴棱
∴棱![]() 的长为4。——8分
的长为4。——8分
(2)由(1)知,M点即为AE1与A1D的交点,由题意显然∠MAD即为所求。——10分
又∠MAD=∠AE1A1∴![]() ——12分
——12分
∴直线![]() 与平面
与平面![]() 所成的角的大小是
所成的角的大小是![]() 。——13分
。——13分
20. 解:(1)![]()
![]() 在(0,
在(0,![]() )上为增函数 2分
)上为增函数 2分
(2)![]() 在(1,
在(1,![]() )上恒成立
)上恒成立
设![]()
则![]() 在(1,
在(1,![]() )上恒成立
)上恒成立
![]()
![]() 在[1,
在[1,![]() )上单调递增
)上单调递增
![]() 5分
5分
故![]() 即
即![]()
![]() 的取值范围为(
的取值范围为(![]() ,3) 7分
,3) 7分
(3)由题意知![]() 时,由(1)知
时,由(1)知![]() 在(0,
在(0,![]() )上单调递增
)上单调递增
![]() ,
,![]() 有两个不相等的正根
有两个不相等的正根
即![]() 有两个不相等的正根m,n 10分
有两个不相等的正根m,n 10分
![]()
![]() 12分
12分
21.解:(1)法一,∵![]()
![]() 当
当![]() 时,
时,![]()
![]()
![]() (3分)
(3分)
法二,由![]() 可知点G在直线y=x上
可知点G在直线y=x上
∴FG的最小值为点F到直线y=x的距离,即![]()
![]() (
(![]() )
)
(2)由![]() 知
知![]() 又
又![]()
![]() (4分)
(4分)
又![]() (
(![]() )∴
)∴![]() ∴点P在以F为焦点,
∴点P在以F为焦点,![]() 为准线的椭圆上
为准线的椭圆上
设P(x,y),则![]() (6分)∵动点P的轨迹C经过点B(0,-1)且
(6分)∵动点P的轨迹C经过点B(0,-1)且![]()
∴![]() 从而b=1(7分) ∴曲线C的方程为:
从而b=1(7分) ∴曲线C的方程为:![]() (8分)
(8分)
(3)设直线![]() 的方程为
的方程为![]()
由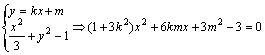 (9分)
(9分)
∵![]() 与曲线C交于不同两点,∴
与曲线C交于不同两点,∴![]() ,即
,即![]() ①(10分)
①(10分)
设![]() 的中点
的中点![]() 由
由![]() 则有BR⊥MN
则有BR⊥MN
∵KMN=KL=K∴![]() (11分)由韦达定理有
(11分)由韦达定理有![]()
∴![]() ∴MN的中点R0坐标为
∴MN的中点R0坐标为![]() (12分)又B(0,-1)
(12分)又B(0,-1)
∴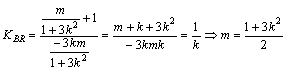 ②
②
由①②联立可得![]()
![]() 即
即![]() (13分)
(13分)
22. 解:(1)设![]() ,将点(0,10)代入后,得c=10
,将点(0,10)代入后,得c=10
![]()
已知![]() ,所以
,所以![]()
所以![]() 4分
4分
![]() 在(1,2]上的值域为[4,6),所以
在(1,2]上的值域为[4,6),所以![]()
![]() 在(2,3]上的值域为(
在(2,3]上的值域为(![]() ,4],所以
,4],所以![]() 6分
6分
当![]() 时,
时,![]() 在(n,n+1]上单调递增,其值域为(
在(n,n+1]上单调递增,其值域为(![]() ]
]
所以![]()
所以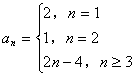 8分
8分
(2)令![]() ,则
,则![]() 10分
10分
当![]() 时,
时,![]()
![]()
![]()
![]()
![]() 13分
13分