解析几何题怎么解
安振平
高考解析几何试题一般共有4题(2个选择题, 1个填空题, 1个解答题), 共计30分左右, 考查的知识点约为20个左右. 其命题一般紧扣课本, 突出重点, 全面考查. 选择题和填空题考查直线, 圆, 圆锥曲线, 参数方程和极坐标系中的基础知识. 解答题重点考查圆锥曲线中的重要知识点, 通过知识的重组与链接, 使知识形成网络, 着重考查直线与圆锥曲线的位置关系, 求解有时还要用到平几的基本知识, 这点值得考生在复课时强化.
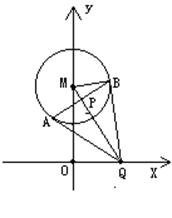
例1 已知点T是半圆O的直径AB上一点，AB=2、OT=t (0<t<1)，以AB为直腰作直角梯形
，使
垂直且等于AT，使
垂直且等于BT，
交半圆于P、Q两点，建立如图所示的直角坐标系.
(1)写出直线的方程；
（2）计算出点P、Q的坐标；
（3）证明：由点P发出的光线，经AB反射后，反射光线通过点Q.
讲解: 通过读图, 看出
点的坐标.
(1 ) 显然
, 
于是 直线
的方程为
；
（2）由方程组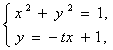
解出 
、
；
（3）
,
.
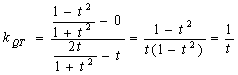由直线PT的斜率和直线QT的斜率互为相反数知，由点P发出的光线经点T反射，反射光线通过点Q.
需要注意的是, Q点的坐标本质上是三角中的万能公式, 有趣吗?
例2
已知直线l与椭圆
有且仅有一个交点Q，且与x轴、y轴分别交于R、S，求以线段SR为对角线的矩形ORPS的一个顶点P的轨迹方程．
讲解：从直线
所处的位置, 设出直线的方程,
由已知，直线l不过椭圆的四个顶点，所以设直线l的方程为
代入椭圆方程
得
化简后，得关于
的一元二次方程
于是其判别式
由已知，得△=0．即
①
在直线方程
中，分别令y=0，x=0，求得
令顶点P的坐标为（x，y）， 由已知，得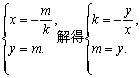
代入①式并整理，得
, 即为所求顶点P的轨迹方程．
方程形似椭圆的标准方程, 你能画出它的图形吗?
例3已知双曲线
的离心率
，过
的直线到原点的距离是
（1）求双曲线的方程；
（2）已知直线
交双曲线于不同的点C，D且C，D都在以B为圆心的圆上，求k的值.
讲解：∵（1）
原点到直线AB：
的距离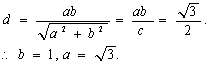
.
故所求双曲线方程为 
（2）把
中消去y，整理得 
.
设
的中点是
，则
即
故所求k=±
.
为了求出
的值, 需要通过消元, 想法设法建构的方程.
例4 已知椭圆C的中心在原点，焦点F1、F2在x轴上，点P为椭圆上的一个动点，且∠F1PF2的最大值为90°，直线l过左焦点F1与椭圆交于A、B两点，△ABF2的面积最大值为12．
（1）求椭圆C的离心率；
（2）求椭圆C的方程．
讲解：（1）设
, 对
由余弦定理, 得
，
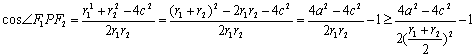
解出 
（2）考虑直线的斜率的存在性，可分两种情况：
i) 当k存在时，设l的方程为
………………①
椭圆方程为
由 得 
.
于是椭圆方程可转化为 
………………②
将①代入②，消去
得 
,
整理为的一元二次方程，得
.
则x1、x2是上述方程的两根．且
，
|
，
AB边上的高
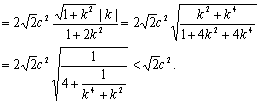
ii) 当k不存在时，把直线
代入椭圆方程得
由①②知S的最大值为
由题意得
=12 所以
故当△ABF2面积最大时椭圆的方程为： 
下面给出本题的另一解法,请读者比较二者的优劣：
设过左焦点的直线方程为：
…………①
（这样设直线方程的好处是什么？还请读者进一步反思反思.）
椭圆的方程为：
由
得：
于是椭圆方程可化为：
……②
把①代入②并整理得：
于是
是上述方程的两根.
,
AB边上的高
,
从而
当且仅当m=0取等号，即
由题意知
, 于是 
.
故当△ABF2面积最大时椭圆的方程为：
例5 已知直线
与椭圆相交于A、B两点，且线段AB的中点在直线
上.
（１）求此椭圆的离心率；
（2 ）若椭圆的右焦点关于直线的对称点的在圆
上，求此椭圆的方程.
讲解:（1）设A、B两点的坐标分别为
得
,
根据韦达定理，得
∴线段AB的中点坐标为（
）.
由已知得
故椭圆的离心率为
.
（2）由（1）知
从而椭圆的右焦点坐标为
设
关于直线的对称点为
解得 
由已知得 
故所求的椭圆方程为
.
例6 已知⊙M：
轴上的动点，QA，QB分别切⊙M于A，B两点，
（1）如果
，求直线MQ的方程；
（2）求动弦AB的中点P的轨迹方程.
讲解:（1）由，可得
由射影定理，得 
在Rt△MOQ中，
|
，
故
，
所以直线AB方程是
（2）连接MB，MQ，设
由
点M，P，Q在一直线上，得
由射影定理得
即
把（*）及（**）消去a，并注意到
，可得
适时应用平面几何知识，这是快速解答本题的要害所在，还请读者反思其中的奥妙.
例7
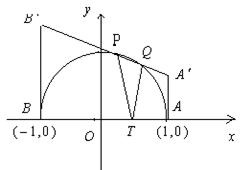
如图，在Rt△ABC中，∠CBA=90°，AB=2，AC=
。DO⊥AB于O点，OA=OB，DO=2，曲线E过C点，动点P在E上运动，且保持 PA + PB 的值不变.
（1）建立适当的坐标系，求曲线E的方程；
（2）过D点的直线L与曲线E相交于不同的两点M、N且M在D、N之间，设
，
| |
| |
|
试确定实数
的取值范围．
讲解: （1）建立平面直角坐标系, 如图所示 .
∵ PA + PB = CA + CB
y
|
|
∴动点P的轨迹是椭圆 .
∵
∴曲线E的方程是
.
（2）设直线L的方程为
, 代入曲线E的方程
，得
设M1（
, 则
|
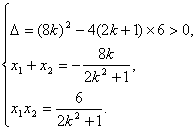
i) L与y轴重合时，
ii) L与y轴不重合时，
由①得 
又∵
,
∵
或 
∴0＜＜1 ,
∴
.
∵
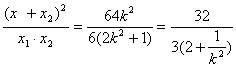
而
∴
∴ 
∴ 
, 
,
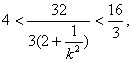
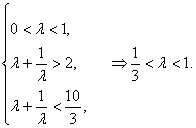
∴的取值范围是
.
值得读者注意的是，直线L与y轴重合的情况易于遗漏，应当引起警惕.
例8
直线过抛物线
的焦点，且与抛物线相交于A
两点.
（1）求证：
;
（2）求证：对于抛物线的任意给定的一条弦CD，直线l不是CD的垂直平分线.
讲解: （1）易求得抛物线的焦点
.
若l⊥x轴，则l的方程为
.
若l不垂直于x轴，可设
,代入抛物线方程整理得
.
综上可知 .
（2）设
，则CD的垂直平分线
的方程为
假设过F，则
整理得
，
.
这时的方程为y=0，从而与抛物线
只相交于原点. 而l与抛物线有两个不同的交点，因此与l不重合，l不是CD的垂直平分线.
此题是课本题的深化，你能够找到它的原形吗？知识在记忆中积累，能力在联想中提升. 课本是高考试题的生长点，复课切忌忘掉课本！
例9 某工程要将直线公路l一侧的土石，通过公路上的两个道口A和B，沿着道路AP、BP运往公路另一侧的P处，PA=100m，PB=150m，∠APB=60°，试说明怎样运土石最省工？
讲解: 以直线l为x轴，线段AB的中点为原点对立直角坐标系，则在l一侧必存在经A到P和经B到P路程相等的点，设这样的点为M，则
MA+AP=MB+BP,
即 MA－MB=BP－AP=50,
,
∴M在双曲线
的右支上.
故曲线右侧的土石层经道口B沿BP运往P处，曲线左侧的土石层经道口A沿AP运往P处，按这种方法运土石最省工.
相关解析几何的实际应用性试题在高考中似乎还未涉及，其实在课本中还可找到典型的范例，你知道吗？
解析几何解答题在历年的高考中常考常新, 体现在重视能力立意, 强调思维空间, 是用活题考死知识的典范. 考题求解时考查了等价转化, 数形结合, 分类讨论, 函数与方程等数学思想, 以及定义法, 配方法, 待定系数法, 参数法, 判别式法等数学通法.