高三数学参考答案

高三数学参考答案

一、选择题：每小题5分，共60分

　1～5：ABACB　　　　　6～10：BBBAC　 11：D　 12：A

二、填空题：每小题4分，共16分

 13．5　　 14．　　 15．　　 16．②

三、解答题：共74分

17．解：(1)令，则

　　　　(2)为奇函数

　　　　  证明：令，由题意得：

　　　　　　　 

　　　　　　　 

　　　　　　　  又∵，故

　　　　　　　 

　　　　　　　  ∴

　　　　　　　  ∴ 为奇函数

　　　　(3)设任意x₁，x₂Î(-¥，0)且x₁ < x₂

　　　　　 则-x₁ > -x₂ >0

　　　　　 又∵在x > 0时是增函数

　　　　　 ∴

　　　　　 又∵是奇函数

　　　　　 ∴

　　　　　 ∴

　　　　　 ∴ 在x < 0时也是增函数

18．解：记“甲译出密码”为事件A，“甲译不出密码”为事件；“乙译出密码”为事件B，“乙译不出密码”为事件．

　  (1)“有且只有甲一人译出密码”为事件A₁，则由于甲、乙两人独立地破泽密码，为相互独立事件，所以事件A₁发生是指事件A和同时发生．从而有

　 

　  (2)“甲和乙至多有一人译出密码”为事件A₂，则事件A₂的对立事件是“甲、乙两人都译出密码”．即，从而有

　 

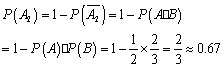
　  (3)（文）设至少需要n个人，则由于n个像乙这样的人都译不出密码的概率为，根据题意得，n个像乙这样的人译出密码的概率满足

　　 ，即，(n Î N *)．

　  解得n ³ 5，且n Î N *．

　  因此至少需要5个像乙这样的人．

　  （3）（理）x 的取值为0，1，2，并且

　　　　

　　　　

　　　　

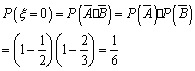
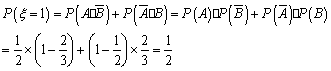
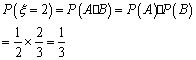
　　　　从而有

19．解：(1)∵A₁B^AE　 ∴A₁C^AE (三垂线定理)

　　　　　 同理 A₁C^AF　 又∵ AE I AF=A

　　　　　 ∴ A₁C^平面A₁EF

　　　　(2)连结BD，过点A作AM^BD，则M为BD的中点，过M作MN^EF，连结AN，则ÐANM即为二面角A-EF-B的平面角

　　　　　 ∵ AE^BA₁，AF^DA₁，且四棱柱为正四棱柱

　　　　　 ∴ BE　DF　又∵ MN^EF

　　　　　 ∴ MN　EF

∵ AE^A₁B

∴ △A₁AB∽△EBA

∴ 　　 

∴

∴二面角A-EF-B的大小为

　　　　(3)设B₁到平面AEF的距离为h，

　　　　  则

　　　　  AN^EF　　

　　　　  ∴

　　　　　　

　　　　  ∴

　　　　  ∴ B₁到平面AEF的距离为

21．解：(1) ∵

∴

 即

∵ 　 ∴

∴

　　　　(2)令，得

　　　　　 求导得：，

令

∴

t	(-¥，-1)	-1	(-1，1)	1	(1，+¥)
	+	0	–	0	+
	~	，极大	‚	，极小	~