湖南师大附中2005—2006学年度高三年级月考试题数学（文）

湖南师大附中2005—2006学年度高三年级月考试题

数学（文科）

说明：本卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.考试时间120分钟，满分150分.

第Ⅰ卷（选择题　共50分）

一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中有且只有一项是符合题目要求的.

1．若是正数的充要条件是　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　 B．　　　　　　　 C．　　　　D．

2．已知m、n为异面直线，m//平面α，n//平面α，直线，则　　　　　　 （　　）

　　　 A．l与α一定垂直　　　　　　　　　　　　　　　　　 B．l与α不一定垂直

　　　 C．l与α一定不垂直　　　　　　　　　　　　　　　 D．l与α可能平行

3．设全集I=R，则集合

　 等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．C_IP　　　　　　　　　　 B．C_IQ　　　　　　　　　　 C．　　　　　　　　　　　 D．（C_IP）∪（C_IQ）

4．某校有高中学生900人，其中高一年级300人，高二年级200人，高三年级400人，现采用分层抽样法抽取一个容量为45的样本，那么高一、高二、高三年级抽取的人数分别为　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．15，5，25　　　　　B．15，15，15　　　　 C．10，5，30　　　　　D．15，10，20

5．在等差数列{a_n}中，若则S₁₅=　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．150　　　　　　　　　　 B．37　　　　　　　　　　　 C．75　　　　　　　　　　　D．不能确定

6．已知实数的运动轨迹是（　　）

　　　 A．抛物线　　　　　　　 B．双曲线　　　　　　　　C．椭圆　　　　　　　　　 D．圆

7．设函数f(x)是可导函数，并且　　　　　（　　）

　　　 A．　　　　　　　　　　　B．－1　　　　　　　　　　 C．1　　　　　　　　　　　　D．－2

8．已知f(x)是奇函数，且当x>0时，的解析式是（　　）

　　　 A．　　　　　B．　　　　　　 C．　　　　　D．

9．设函数，现将函数的图象向左平移2个单位，再关于x轴对称后所对应函数的反函数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　　　D．

10．给出下列4个命题：

　　　 ①若sin2A=sin2B，则△ABC是等腰三角形；

　　　 ②若sinA=cosB，则△ABC是直角三角形；

　　　 ③若cosAcosBcosC<0，则△ABC是钝角三角形；

　　　 ④若cos(A－B)cos(B－C)cos(C－A)=1，则△ABC是等边三角形.

　　其中正确的命题是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．①③　　　　　　　　　 B．③④　　　　　　　　　 C．①④　　　　　　　　　 D．②③

第Ⅱ卷（非选择题共100分）

二、填空题：本大题共5小题，每小题4分，共20分.

11．在四个数中，最大的数是　　　　 　 .

12．已知=　　　　　  .

13．已知函数　　　 .

14．已知异面直线a，b所成的角为40°，过空间一定点P且与a、b所成的角都是70°的直线共有　　　　　 条.

15．已知下列命题：

　　①；

　　　 ②若向量按向量平移后的坐标仍是（－3，4）；

　　　 ③“向量的方向相反”是“互为相反向量”的充分不必要条件；

　　　 ④已知点M是△ABC的重心，则

　　其中正确命题的序号是　　　　　　 .

三、解答题：本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.

16．（12分）已知为锐角，且的值.

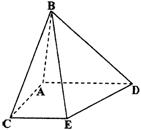
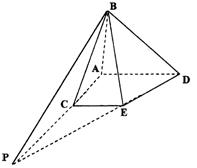
17．（12分）如图，在多面体ABCDE中，△ABC为正三角形，四边形ACED为梯形，AD//CE，AD⊥AC，AD=AC=2CE=2，BD=.

　 （Ⅰ）求证：平面ACED⊥平面ABC；

　 （Ⅱ）求平面DBE与平面ABC所成二面角（锐角）的大小.

18．（14分）已知函数的切线方程为y=3x+1，且函数处有极值.

　 （Ⅰ）求的表达式；

　 （Ⅱ）求函数在[－3，1]上的最大值.

19．（14分）澳门有一种博彩游戏，其规则如下：庄家在口袋里装黑、白围棋子各8枚，博彩者从中随机一次摸出5枚，摸一次交手续费1元，中彩情况如下：

摸子情况	5枚白	4枚白	3枚白	其它
彩　　金	20元	2元	纪念品价值5角	无奖

　 （Ⅰ）分别求博彩一次获20元彩金，2元彩金，纪念品的概率；

　 （Ⅱ）如果游客博彩1000次，庄家是赔钱还是赚钱？金额约是多少元？（精确到元）

20．（14分）已知椭圆C的中心在坐标原点，一个焦点为F（0，－），对应的准线方程为

　 （Ⅰ）求椭圆C的方程；

　 （Ⅱ）是否存在直线l，使l与椭圆C交于不同的两点M，N，且使线段MN恰好被直线平分？若存在，求l的倾斜角θ的取值范围，若不存在，说明理由.

21．（14分）某种产品具有一定的时效性，在这个时效期内，由市场调查可知：在不作广告宣传且每件获利a元的前提下可卖出b件；若作广告宣传，广告费为n（n∈N*）千元时比广告费为n－1千元时多卖出件.设作n千元广告时的销售量为S_n.

　 （Ⅰ）试写出销售量S_n与n的函数关系式；

　 （Ⅱ）当a=10，b=4000时，厂家应生产多少件这种产品，做几千元广告，才能获取最大利润？

高三数学（文）参考答案

一、选择题：

1.D  2.A　3.B　4.D  5.C　6.A　7.C  8.B　9.A　10.B

二、填空题

11．　12．　 13．2　　14．3　 15．②④

① ②

三、解答题：

16．解：由

∵

①÷②　得　即  …………6分

又∵，∴

∴.　…………12分

17．（1）证明：在△ABD中，AB=AD=2，BD=　∴AD⊥AB.…………2分

∵AD⊥AC　又AC∩AB=A， ∴AD⊥平面ABC　…………4分

又∵AD平面ACED， ∴平面ACED⊥平面ABC …………6分

（2）解：延长DE，AC交于P，连结BP，

则BP是平面ABC与平面BDE的交线.

∵CE//AD　，　∴C是AP中点，

且PC=AC=BC.　∴△ABP为直角三角形，

∠PBA=90°，且AB⊥BP …………8分

又∵AD⊥平面ABC， ∴BD⊥BP　 ……10分

∴∠DBA是平面DBE与平面ABC所成

二面角的平面角.

故平面DBE与平面ABC所成角为45°.　…………12分

18．（1）由

过的切线方程为：

 …………2分

而过

① ②

故　　  …………4分

∵　③ …………5分

由①②③得  a=2，b=－4，c=5.

∴　 ………………7分

（2）

当

　…………12分

又在[－3，1]上最大值是13.　…………14分

19．（1）一次摸奖中20元彩金的概率　…………2分

一次摸奖中2元彩金的概率　…………5分

中纪念奖概率 　…………7分

（2）1000次收手续费1000元.

预计支付20元奖需；…………9分

支付2元奖需元； …………11分

支付纪念奖需元；　…………13分

则余额n=1000－m₂₀－m₂－m_纪=308元

答：庄家赚钱约308元.　 …………14分

20．（1）设椭圆方程为　 …………2分

由题意

∴椭圆方程为　 …………6分

（2）设存在直线l：y=kx+b.故椭圆交于M，N，线段MN中点为

由　※　…………8分

由方程※判别式　

得　　①　…………10分

又　代入①

解得 　 …………12分

∴　 …………14分

21．（1）据题意

　………………4分

上述各相加，得　

即　　 …………7分

（2）b=4000时，　　  设销售量S_n时获利T_n，则有

　…………10分

欲使T_n最大，则　…………12分

此时S_n=7875.

故该厂家生产7875件产品，使5千元的广告，能使获利更大. ……14分