数学(理科)答案
一、D A C D B C C C D B C A
二、13.![]() ;14. an=
;14. an=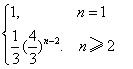 ;15. 22006 ;16.
①、③.
;15. 22006 ;16.
①、③.
三、17. ![]() ,
,
![]() ,
,
![]()
![]() ,
,![]()
![]() , 故
, 故![]() ,
,
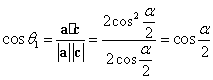 ,
,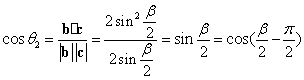
![]() ,又
,又![]() ,
,
![]()
![]() ,故
,故![]() ,
,![]()
![]()
18. 由![]() 得
得![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ;当
;当![]() ≥1时,
≥1时,![]()
![]() ,
,
又![]() 的单调递增区间为
的单调递增区间为![]() ,
,
显然,当![]() ≥1时,
≥1时,![]() 在
在![]() 上不可能是增函数, 因此, 当
上不可能是增函数, 因此, 当![]() ,要使
,要使![]() 在
在
![]() 上是增函数,只有
上是增函数,只有![]() ,
,
所以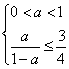 ,解得
,解得![]() ≤
≤![]() ,故
,故![]() 的范围为
的范围为![]() ≤
≤![]() .
.
19. 设矩形温室的左侧边长为a m,后侧边长为bm,则ab = 800![]() .
.
蔬菜的种植面积![]() .
.
![]() .
.
当![]() , 即
, 即![]() 时,
时, ![]() .
.
答:当矩形温室的左侧边长为40m,后侧边长为20m时,蔬菜的种植面积最大,最大种植面积为648![]() .
.
20.(1)当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() .
.
故当![]() 时,
时,![]() 的表达式为
的表达式为
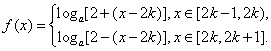
(2)∵![]() 是以2为周期的周期函数,且为偶函数,∴
是以2为周期的周期函数,且为偶函数,∴![]() 的最大值就是当
的最大值就是当![]() 时,
时,![]() 的最大值.∵
的最大值.∵![]() ,∴
,∴![]() 在
在![]() 上是减函数,
上是减函数,
∴![]() ,∴
,∴![]() .
.
当![]() 时,由
时,由![]() 得
得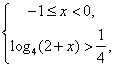 或
或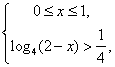
得![]() .
.
∵![]() 是以2为周期的周期函数,
是以2为周期的周期函数,
∴![]() 的解集为
的解集为![]() .
.
21. 椭圆方程为![]() .
.
![]()
![]() ,
,![]() .
.
设PQ的方程为![]() ,代入椭圆方程消去
,代入椭圆方程消去![]() 得
得![]() .
.
设![]() ,则
,则![]()
![]() .
.
(Ⅰ)当![]() 时,MN的斜率为
时,MN的斜率为![]() ,同理可得
,同理可得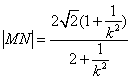 ,
,
故四边形面积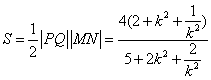 .
.
令![]() ,则
,则![]() ,即
,即![]()
当![]() 时,
时,![]() .且S是以
.且S是以![]() 为自变量的增函数,
为自变量的增函数,![]()
![]() .
.
(Ⅱ) 当![]() 时,MN为椭圆的长轴,
时,MN为椭圆的长轴,![]()
![]()
![]()
综合(Ⅰ) (Ⅱ)知,四边形PQMN面积的最大值为![]() ,最小值为
,最小值为![]() .
.
22. 解:(1)![]()
![]() ,且每横行成等差数列,
,且每横行成等差数列,
![]()
![]() ,
,
![]()
![]() ,又
,又![]()
![]()
![]() (
(![]() )
)
![]()
![]() ;
;
(2)![]()
=![]()
![]() ①
①
![]()
![]()
![]() ②
②
②-①得 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.