涟源市行知中学2006届11月份月考
文 科 数 学 试 题
命题：李杰红 时间：120分钟
第Ⅰ卷(选择题 共50分)
一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只
有一项是符合题目要求的，请将答案填在答卷纸相应表格中.
1、 p: 如果x2+2x+1－a2<0,那么－1+a<x<－1－a. q: a<1. 那么，q是p的（ ）
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
2、 已知函数
是奇函数, 则函数
的图象关于 ( )
A.
直线
对称 B. 直线
对称
C. 点
对称 D. 点
对称
3、一套共7册的书计划每2年出一册，若各册书的出版年份数之和为13979，则出齐这套书的年份是 ( )
A. 2005 B. 2003 C. 2001 D. 1999
4、若
是等差数列，
是其前
项和，
，
，则
，
，
，…，中最小的是
（ ）
A．
B．
C．
D．
5、函数
的 （ ）
A．最大值是2，最小值是
B．最大值是1，最小值是
C．最大值是2，最小值是
D．最大值是1，最小值是
6、已知
，
，且
与
平行，则
（ ）
A．
；
B．
；
C．
；
D．
.
7、 已知
,则下列各式中正确的是（ ）
A.
B. 
C. 
D. 
8、实数
（ ）
A、10 B、9 C、
D、
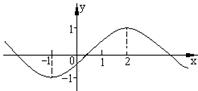9、已知函数
的图象如图所示, 则函数
的单调递减区间是 ( )
A. 
B. 
C. 
D. 
10、某公司从2003年起每人的年工资由三个项目组成，并按下表规定实施
| 项 目 | 计 算 办 法 |
| 基础工资 | 2003年1万元，考虑物价因素，以后每年递增10% |
| 住房补贴 | 按工龄计算：400元×工龄（工龄计算办法：如某职工2001年进公司，到2004年按4年计算） |
| 医 疗 费 | 每年1600元固定不变 |
该公司的一名职工在2005年得到的住房补贴和医疗费之和可超过基础工资的25%，则这位职工的工龄至少是 （ ）
A．5年 B．4年 C．3年 D． 2年
第Ⅱ卷 (非选择题 共100分)
二. 填空题：本大题共5小题，每小题4分，共20分，请将答案填在答卷相应横线上。
11．向量
、
为单位向量，且
，则与
的夹角为
.
12．二次函数
满足
，且
，则实数
的
取值范围是 ______________.
13. 将函数
的图象按向量
（其中
）平移后与
的图象重合,则向量坐标
,
.
14、对于满足0≤
≤4的实数，使
恒成立的
的取值范围是 ．
15、在
中，O为中线AM上一个动点，若AM=2，则
的最小值是________．
涟源市行知中学2006届11月份月考
数 学 答 卷
一、选择题：本大题共10小题，每小题5分，共50分.
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、 填空题：本大题共5小题，每小题4分，共20分.
11.
_______
12._____________________ 13. ____ ,_______
14.____________________ 15. __________
三、解答题（共80分）
16.（12分）已知：
、
、
是同一平面内的三个向量，其中 ＝（1，2）
⑴
若
，且
，求的坐标；
⑵
若=
且与垂直，求与的夹角θ.
17．（12分）已知
，
，方程
有两个不等实根
. ①求实数的取值范围; ②求
的值.
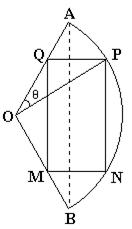
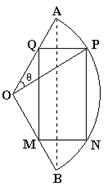18．（13分）某校在申办国家级示范校期间，征得一块形状为扇形的土地用于建设田径场，如图所示。已知扇形角
，半径OA=120米，按要求准备在该地截出内接矩形MNPQ，并保证矩形的一边平行于扇形弦AB，设
，记
。
（1）以
为自变量，写出
关于的函数关系式；
（2）当为何值时，矩形田径场的面积最大，并求最大面积。
19.（13分）（1）已知
是正常数，
，
，求证：
，指出等号成立的条件；
（2）利用（1）的结论求函数
（
）的最小值，指出取最小值时的值．
20.(本大题满分14分) 轻纺城的一家私营企业主，一月初向银行贷款一万元作开店基金，每月月底获得的利润是该月初投入资金的
，每月月底需要交纳房租和所得税为该月所得金额（包括利润）的
，每月的生活费开支300元，余款作为资金全部投入再经营，如此继续，问该年年底，该私营企业主有现款多少元（结果保留一位小数）？如果银行贷款的年利率为
，问私营企业主还清银行贷款后纯收入还有多少元（结果保留一位小数）？
(参考数据：
，
，
)
21．（16分）设
的图象上任意两点，且
，已知点M的横坐标为.
（I）求证：M点的纵坐标为定值；
（Ⅱ）若
,其中
；
（Ⅲ）已知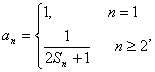
是否存在实数
，对于任意
，都有
恒成立,若存在,求出的值（或取值范围）；若不存在，请说明理由.
参考答案
一、选择题: 每小题5分，共50分 1-5 ACBBA 6-10 CDABB
二. 填空题：每小题4分，共20分11.
12. 
13. 
1
14、
15. –2
三、解答题（共80分）
16、(12分)解：⑴设
由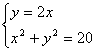
∴
或 
∴
…………6分
⑵
……（※）
代入（※）中,
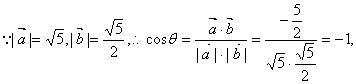
…………12分
17．(12分)解：（1）
……2分
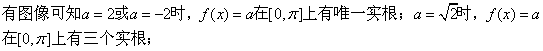
……8分
由图像知
……12分
18．解：（1）
在△OQP中，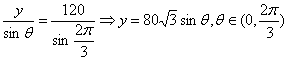
----------------------------4分
（2）作
于H，
，
或先求
，由余弦定理求
，或连结ON，用余弦定理直接求PN，
此时，
。
---------------------------------------------------------10分
（注：也可得到S
）
所以当
时，
。
答：当
时，矩形田径场的面积最大，最大面积为
平方米。---------13分
19、(14分)⑴
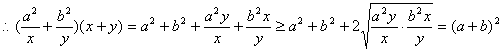……4分
故 当且仅当
时取等号 ………7分
（2）由得
………11分
当且仅当
时，即
时，
………13分
20(14分):解:设每月月底的现款构成的数列为
,且
…………2分
………6分
成等比,且首项为
公比为1.08 ………8分
………9分
(元) ………11分
还贷后纯收入为
(元)
答:略 ………14分
21．（本小题满分16分）
（I）证明：
M是AB的中点，设M点的坐标为（x，y）
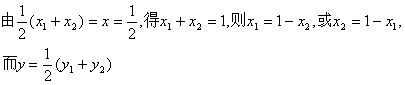……………2分
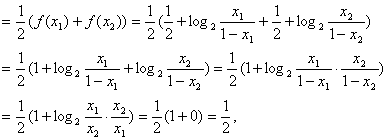
∴M点的纵坐标为定值. ……………………5分
（II）解：由（I）知
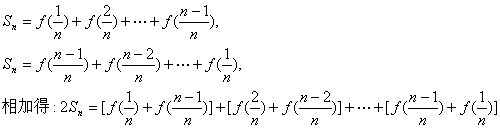
……………………8分
. ……………………10分
（Ⅲ）依题意：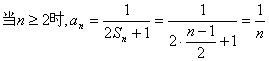
，……………………11分
……………………12分
. ……………………15分
故存在
成立. ……………………16分