兰州铁一中2005－2006学年第一学期高三数学期中考试（含答案）

兰州铁一中2005－2006学年第一学期期中考试

高三数学

一、选择题：(每题5分，共60分，将正确答案的序号填在后面的答题卡上。)

1.　　　　 已知非空集合M，N，定义M－N={xx∈M，xN}，那么M－（M－N）=………（　　）

(A)M∪N 　　　　　 (B) M∩N　　　　　　　(C)M　　　　　　  (D) N

2.　　　　 不等式(x－1)的解为…………………………………………………（　　）

(A)x≥1　　　　　　　(B)x>1　　　　　　　(C) x≥1或者x=－2　 (D) x≥－2且x≠1

3.　　　　 =2k+（k是整数）”是“tan=tan”的………………………………………（　　）

　　(A)充分不必要条件　(B)必要不充分条件　

(C)充要条件　　　　(D)既不充分条件也不必要条件

4.　　　　 函数f（x）的值域为[－2，2]，则函数f（x＋1）的值域为……………………………（　　）

(A)[－1，3]　　　 　 (B)[－3，1]　　　　　 (C)[－2，2]　　　　  (D)[－1，1]

5.　　　　 ，则=…………………………………（　　）

(A)3+2　　　　(B) 3－2　　　　  (C) 1+　　　　 (D) 1－

6.　　　　 已知的图象经过点(4,0),而且其反函数的图象过点(1,7),则f(x)是 …………………………………………………………………………………(　　 )

(A)增函数　　　　  (B) 减函数　　　　  (C) 奇函数　　　　　　 (D) 偶函数

7.　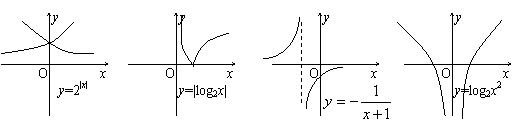　　　 下列函数，分别对应四个图象，其中解析式与图象对应错误的是……………………………………………………………………………………（　　）

(A)　　　　　　　 (B)　　　　　　　　  (C)　　　　　　　　 (D)

8.　　　　 方程与mx+ny=1在同一坐标系内的图象为………………………（　　）

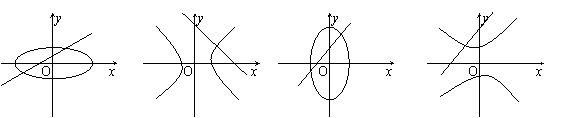(A)　　　　　　　　  (B)　　　　　　　  (C)　　　　　　　　　 (D)

9.　　　　 若数列的前四项为2，0，2，0，则这个数列的通项公式不能是……………………（　　）

（A）a_n＝1＋(－1)^n－1（B）a_n＝1－cosnp

（C）a_n＝2sin² 　　　　　　　　　　（D）a_n＝1＋(－1)^n－1＋(n－1)(n－2)

10.　　 三点A（x₁，y₁），B（x₂，y₂），C（x₃，y₃）共线的充要条件是　　　　　　　　　　　　　　　　（ 　 ）

　　　 A．x₁y₂－x₂y₁=0　　　　　　　　　　　　　　　　　　　 B．（x₂－x₁）（y₃－y₁）=（x₃－x₁）（y₂－y₁）

　　　 C．x₁y₃－x₃y₁=0　　　　　　　　　　  D．（x₂－x₁）（x₃－x₁）=（y₂－y₁）（y₃－y₁）

11.　　 1＞x＞0，下列三个数：a=，b=1＋x，c=，则其中最大的一个是………………（　　）

(A)a　　　　　　　　  (B) b　　　　　　　　(C) c　　　　　　　　 (D) 不能确定

12.　　 十个人站成一排，其中甲、乙、丙三人恰巧站在一起的概率为…………………………（　　）

（A）　　 （B）　　 （C）　　  （D）

二、填空题：(每題4分，共16分，将正确答案填在后面的答题卡上)

13.　　 如果不等式的解集为R，则实数k的取值范围是　　　　　　  .

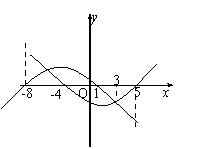
14.　　 已知函数、y=的图象如图，则·>0 的解集为　　　　　　　　　　　  ；

15.　　 函数的单调递减区间为　　　　　　　 .

16.　　 函数y=f(x)=x³+ax²+bx+a²，在x=1时，有极值10，那么的值为_______.

兰州铁一中2005－2006学年第一学期期中考试高三数学

班级___________　 姓名___________　 成绩____________

一、选择题：(每题5分，共60分)

题号	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.
答案

二、填空题：(每題4分，共16分)

13、__________________　　　 14、__________________

15、__________________　　　 16、__________________

三、解答题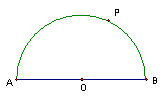：(74分)

17.　　 (12分)AB=r是单位半圆的直径，动点P从A出发先过半圆弧再沿BA回到A点，试把动点P到点A的水平距离S表示为路程x的函数.

18.　　 (12分)定义在R上的奇函数y=f(x)满足x<0时，f(x)=，求函数y=f(x)的表达式并且解方程f(x)=2x.

19.　　 (12分)顶点在原点，焦点在x轴上的抛物线截直线2x－y－4＝0所得的弦长为，求此抛物线的方程.

20.　 (12分)一批货物随17列货车从A地以vkm/h的速度匀速直达B地，已知两地铁路线长400km，为了安全，两货车距离不得小于km，求这批货物全部抵达B地所需要的最少时间！

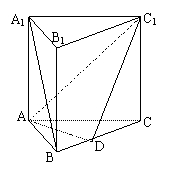
21.　　  (13分)如图正三棱柱ABC－A₁B₁C₁的各棱均相等，D是BC上的一点，AD⊥C₁D

（1）求证：面ADC₁⊥侧面BCC₁B₁

（2）求二面角C－AC₁－D的大小（用反三角函数表示）；

（3）若AB=2，求直线A₁B与截面ADC₁之间的距离

22.　 （13分）已知函数

（1） 求在函数图象上点A处的切线的方程；

（2） 若切线与y轴上的纵截距记为，讨论的单调增区间。

参考答案:

一、

BCDCC　　AADDB  C A

二、

13.0<k<1　　14.(-8,-4)∪(1,3)　　15.(2,3)　 16.—44

三、

17．　

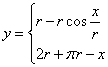
18．-1，0，1

19．　

20．8

21．（1）略　（2）　 （3）

22．（1）

切线的方程：

（2）令x=0，

①　　 当a>0时,由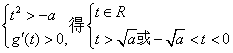

　

②当a=0时,由

③当a<0时,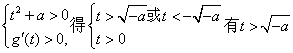

综合①②③当

　　　　  当a=0时,

　　　　 当a<0时,