荆州市2006届高中毕业班质量检查(I)
数 学(文史类)
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率Pn(k)=![]()
第I卷 (选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项正确,每小题选出答案后,用2B铅笔把第Ⅱ卷上端答题卡上对应题目的答案标号涂黑,多涂、不涂或涂错得0分。
1.设A、B为两个非空实数集合,定义集合A·B=![]() ,若A=
,若A=![]() ,则A·B中元素的个数是
,则A·B中元素的个数是
A.6 B.7 C.8 D.9
2.若![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知函数![]() 是定义在R上的偶函数,并且在
是定义在R上的偶函数,并且在![]() 上是单调函数,若
上是单调函数,若![]() =-2,
=-2,![]() ,则使得
,则使得![]() < 0的x 的取值范围是
< 0的x 的取值范围是
A.(![]() )
B.(
)
B.(![]() )
)
C.
![]() D.(-1,1)
D.(-1,1)
4.“![]() ≤0”是“函数y=x2-2ax-3在 [0,1] 上具有单调性”
≤0”是“函数y=x2-2ax-3在 [0,1] 上具有单调性”
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.某工厂生产了一批产品,这批产品分别由甲、乙、丙3个车间完成,为检查这批产品的质量,决定采用分层抽样的方法进行抽样,已知从甲、乙、丙3个车间抽取的个数恰好组成了一个等差数列,且从乙车间抽取的产品数是500件,则这批立品总数是
A.1000 B.1500 C.2000 D.2500
6.函数![]() =
=![]() (0,1)内有极小值,则
(0,1)内有极小值,则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在各项都为正数列![]() 中,首项
中,首项![]() =2,前三项和S3=14,则
=2,前三项和S3=14,则![]()
A.34 B.56 C.72 D.158
8.函数![]() =
=![]() ,则使
,则使![]() < 0的x取值范围是
< 0的x取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.下列函数中既是奇函数,又在区间 [-1,1]上单调递减的是
A.![]() =sinx
B.
=sinx
B.![]() = -x-1
= -x-1
C.![]()
![]() D.
D.![]()
10.当![]() 时,函数
时,函数![]() 的最小值是
的最小值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.函数![]() =
=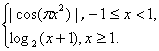 若
若![]() ,则m的所有可能值为
,则m的所有可能值为
A.1,-1 B.1,0,-1
C.![]() D.1,
D.1,![]()
12.已知函数![]() = ax2 + (a2-1)x + a-2 (x > 0)与函数g ( x )= logax 的单调区间相同有相同区间上单调性也相同,其中
= ax2 + (a2-1)x + a-2 (x > 0)与函数g ( x )= logax 的单调区间相同有相同区间上单调性也相同,其中![]() 若
若![]() =m有且仅有两个实数解,则实数
=m有且仅有两个实数解,则实数![]() 和
和![]() 的取值范围分别是
的取值范围分别是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
荆州市2006届高中毕业班质量检查(I)
数 学(文史类)
第Ⅱ卷(非选择题共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13.函数![]() =
=![]() 的定义域是
。
的定义域是
。
14.设函数![]() 的图象关于点(1,3)对称,且存在反函数
的图象关于点(1,3)对称,且存在反函数![]() ,
,![]() ,则
,则![]()
= 。
15.设![]() 是定义在R上的奇函数,且
是定义在R上的奇函数,且![]() ,则
,则![]()
= 。
16.已知数列![]() 满足
满足![]()
![]() =
.
=
.
三、解答题:本大题共6小题,共74分,解答题应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)
已知![]() 的值。
的值。
18.(本小题满分12分)
已知![]() 是公比为q的等比数列,且
是公比为q的等比数列,且![]() 成等差数列。
成等差数列。
(1)求q的值;
(2)设![]() 是以1为首项,q为公差的等差数列,其前n项和为Sn,比较Sn与bn的大小,并说明理由。
是以1为首项,q为公差的等差数列,其前n项和为Sn,比较Sn与bn的大小,并说明理由。
19.(本小题满分12分)
若函数![]() =
=![]() 在区间
在区间![]() 单调递增,求
单调递增,求![]() 的取值范围。
的取值范围。
20.(本小题满分12分)
已知函数![]() 和
和![]() 的图象关于点(0,1)对称,且
的图象关于点(0,1)对称,且![]() =x2 +
2x -1.
=x2 +
2x -1.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() =
=![]()
![]() +1在 [ -1,1]上是增函数,求实数
+1在 [ -1,1]上是增函数,求实数![]() 的取值范围。
的取值范围。
21.(本小题满分12分)
定义在R上的函数![]() 满足
满足![]() =
=![]() ,当
,当![]() [2,6]时,
[2,6]时,![]() =
=![]()
(1)求![]() 在区间[2,6]上的解析式;
在区间[2,6]上的解析式;
(2)比较![]() 与
与![]() 的大小。
的大小。
22.(本小题满分14分)
已知数列![]() 的首项
的首项![]() =4,前n项和为Sn ,且
=4,前n项和为Sn ,且![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设函数![]() =
=![]()
![]()
荆州市2006届高中毕业班质量检查(I)
数学试题(文)参考答案及评分说明
一、BADAB DBDDA BA
二、13.(![]() ,0) 14.
,0) 14.![]() 15.0 16.
15.0 16.![]()
三、17.解:![]()
![]()
![]()
![]()
![]() (4分)
(4分)
![]()
![]()
![]()
![]()
![]() ,
,![]() (8分)
(8分)
![]()
![]() (10分)
(10分)
![]()
![]() (12分)
(12分)
18.解:(1)由题设![]()
即![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() (6分)
(6分)
(2)若![]() ,
,![]() ,
,![]()
显然 由![]() 时,
时,![]() (8分)
(8分)
当![]() ≥2时,
≥2时,![]() 故
故![]()
若![]() ,则
,则![]()
当![]() ≥2时,
≥2时,![]() (10分)
(10分)
故对于![]() ,当2≤
,当2≤![]() ≤5,
≤5,![]() ;
;![]() ,
,![]() ;
;![]() ≥7时,
≥7时,![]() (12分)
(12分)
19.解:令![]() (2分)
(2分)
当![]() 内单调递增 ,必须
内单调递增 ,必须![]() ≥0
≥0
即![]() ≥0
≥0![]() 内恒成立
内恒成立
![]()
![]() ≤
≤![]()
![]()
![]() ≤0与
≤0与![]() >1矛盾
(6分)
>1矛盾
(6分)
当![]() 时,必须
时,必须![]() ≤0,即
≤0,即![]() ≤0
≤0![]() 内恒成立
内恒成立
![]()
![]() ≥
≥![]()
![]() 内恒成立
内恒成立
![]()
![]() ≥
≥![]() (8分)
(8分)
又![]()
![]()
![]() (10分)
(10分)
综上,![]() ≤0 < 1
(12分)
≤0 < 1
(12分)
20.解:设函数![]() 的图象上任一点
的图象上任一点![]() 关于
关于![]() 的对称点
的对称点![]()
![]()
![]()
![]()
![]()
则 ![]() 即
即 ![]()
![]() 在函数
在函数![]() 的图象上
的图象上
![]()
![]() 即
即 ![]()
故![]() (4分)
(4分)
(2)![]()
①当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,![]()
![]() (6分)
(6分)
②![]() 时,其对称轴的方程为
时,其对称轴的方程为 ![]()
![]()
![]()
![]()
![]() ≤
≤ ![]() 或
或 ![]() ≥
≥ ![]()
![]()
![]()
![]()
![]() ≤0
(10分)
≤0
(10分)
综上,![]() ≤0
(12分)
≤0
(12分)
21.解:(1)![]() 在R上满足
在R上满足![]()
![]()
![]() (2分)
(2分)
![]()
![]()
![]()
![]()
![]()
![]() (4分)
(4分)
![]()
![]()
又![]()
![]()
![]()
![]()
![]()
![]() (6分)
(6分)
(2)由(1)知![]()
![]()
![]()
![]()
![]()
![]()
![]() (8分)
(8分)
又![]()
![]()
![]() (10分)
(10分)
![]()
![]()
![]()
![]()
![]() (12分)
(12分)
22.解:① ![]() ≥
≥![]() ①
①
![]()
![]() ≥
≥![]() ②
②
![]() ①—②得
①—②得![]() ≥
≥![]() (2分)
(2分)
又![]()
![]()
![]()
![]()
![]()
![]() ≥
≥![]() (4分)
(4分)
![]()
![]() 为等比数列
为等比数列![]()
![]() (6分)
(6分)
②![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (12分)
(12分)
![]()
![]() (14分)
(14分)
注:解答题若有其它解法,只有思路清晰,方法正确,均可酌情给分。