高三数学(文)全国统一标准测试(四)

绝密 ★ 启用前　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(零四年一月号)

03-04年高三数学(文)全国统一标准测试(四)

命题范围：第九章　直线、平面、简单几何体　第十章　排列、组合与排率

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.

第Ⅰ卷(选择题  共60分)

注意事项：

1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.

2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案.

3.如果不采用答题卡答题，请把第Ⅰ卷（选择题）的答案填入第Ⅱ卷的选择题答题表中.

参考公式：

sinαcosβ=［sin(α+β)+sin(α－β)］　

cosαsinβ=［sin(α+β)－sin(α－β)］

cosαcosβ=－［cos(α+β)+cos(α－β)］　

sinαsinβ=－［cos(α+β)－cos(α－β)］

sinα+sinβ=2sincos　　　　　　

sinα－sinβ=2cossin

cosα+cosβ=2coscos　　　　　　

cosα－cosβ=－2sinsin

S_台侧= (c′+c)l(c、c′分别表示上、下底面周长，l表示斜高或母线长)

V_台体=（S′++S）h(S′、S分别表示上、下底面积，h表示高)

一、选择题（本大题共12小题；每小题5分，共60分.在每小题给出的四个选项中，有一项是符合题目要求的.）

1．若a₁(x－1)⁴+a₂(x－1)³+a₃(x－1)²+a₄(x－1)+a₅=x⁴，则a₂+a₄等于

A.14　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.12　　　　　　　　 

C.10　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　D.8

2．设正四棱锥底面边长为3，体积为，则它的侧面与底面所成角的大小为

A.75°　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.30°

C.45°　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.60°

3．在下列命题中，真命题是

A.若直线m，n都平行于平面α，则m∥n

B.设α－l－β是直二面角，若直线m⊥n, m⊥β，则n⊥α

C.若直线m，n在α内的射影依次是一个点和一条直线，且m⊥n，则n在α内或n与α平行

D.设m，n是异面直线，若m平行于平面α，则n必与α相交

4．已知圆锥的侧面展开图扇形圆心角为180°，则这个圆锥的轴截面顶角为

A.45°　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.120°

C.60°　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.90°

5．如果把两条异面直线看成“一对”，那么六棱锥的棱所在的12条直线中，异面直线共有

A.12对　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.24对

C.36对　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.48对

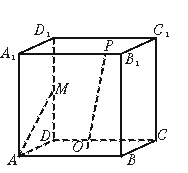6．正方体ABCD－A₁B₁C₁D₁中，M为棱DD₁的中点，O为底面ABCD的中心，P为棱A₁B₁上任一点，则直线OP与直线AM所成角为

A.

B.

C.

D.

7．把英语单词“error”中字母的拼写顺序写错了，则可能出现的错误种数是

A.20　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.19

C.10　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.9

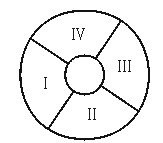
8．中央电视台“正大综艺”节目的现场观众来自四个单位，分别在图中四个区域内坐定.有4种不同种颜色的服装，每个单位的观众必须穿同种颜色的服装，且相邻两个区域的颜色不同，不相邻区域颜色相同与否不受限制，那么不同的着色方法共有_________种

A.24

B.36

C.48

D.84

9．对于不共面的三个向量a，b，c，下列命题正确的是

A.（a·b）²·c=（a²·b²）·c

B.总可以找到两个实数λ、μ，使c=λa+μb

C.这三个向量不能相加

D.对空间任意向量d，存在有序实数组x₁、x₂、x₃、x₄，使x₁d=x₂a+x₃b+x₄c，其中x₁不等于零

10．在有太阳的时候，一个大球放在地面上，球的影子伸到距球与地面的接触点10米处，同一时刻，一根长1米，一端接触地面而垂直于地面的尺子的影子长度是2米，则球的半径是

A.2.5米　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.10－20米

C.6－米　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.9－4米

11．某体育彩票规定：从01~36共36个号中抽出7个号为一注，每注2元.某人想从01~10的10个号中选3个连续的号，从11~20中选2个连续的号，从21~30中选1个号，从31~36中选1个号组成一注，则此人要把满足这种要求的号买全，至少要花

A.3366元　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.6720元

C.4320元　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.8640元

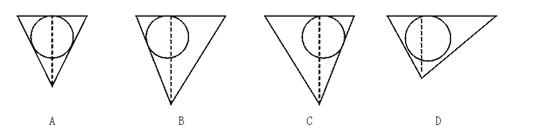
12． 如图，在一个倒置的正三棱锥容器中，放入一个钢球，钢球恰与棱锥的四个面都接触上，经过棱锥的一条侧棱和高作截面，正确的截面图形是

第Ⅱ卷(非选择题  共90分)

二、填空题（本大题共4小题；每小题4分，共16分.把答案填在题中的横线上.）

13.某学生从六门学科A、B、C、D、E、F中选学两门，但A与B，C与D由于时间冲突不能同时选学，则学生可能有的选法有______种.

14．若四面体各棱长是1或2，且该四面体不是正四面体，则其体积的值是______.(只要写出一个可能的值)

15.太阳光线照于地面，与地面成角α(0＜α＜),当长度是定值a的木棍与地面所成角为______时，木棍在地面上的射影最长.

16．甲射击命中目标的概率是，乙射击命中目标的概率是，丙射击命中目标的概率是，现在三人同时射击目标，则目标被击中的概率为______.

三、解答题(本大题共6小题；共74分.解答过程应写出文字说明、证明过程或演算步骤.)

17．（本小题满分12分）

已知整式函数f(x)=(1+x)^m+(1+x)ⁿ(m，n∈N*)的展开式为f(x)=a₀+a₁x+a₂x²+a₃x³+…+a_mx^m,已知a₁=17.　

(1)求f(x)中x²项系数的最小值；

(2)求a₅；

(3)求f(x)中所有x的指数是奇数的项的系数和.

18．（本小题满分12分）

从三棱锥P－ABC（如图1）的顶点沿着三条侧棱PA,PB,PC剪开，成平面图形，得到△P₁P₂P₃（如图2），且P₁P₂=P₂P₃；

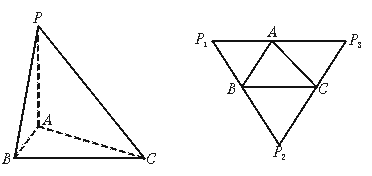
图1　　　　　　　　　　　　　　　　 图2

（1）在棱锥P－ABC中，求证：PA⊥BC；

（2）P₁P₂=26，P₁P₃=20，求三棱锥的体积.

19.（本小题满分12分）

用1，2，3，4，5这五个数组成无重复数字的五位数，按由小到大的顺序排列.

（1）32154是第几个数？

（2）第20个数是几？

20．（本小题满分12分）

有一问题，在半小时内，甲能解决它的概率是0.5，乙能解决它的概率是，如果两人都试图独立地在半小时内解决它，计算：

（1）两人都未解决的概率；

（2）问题得到解决的概率.

21.(本小题满分12分)

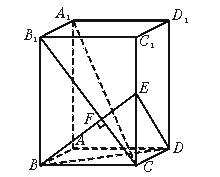
已知长方体AC₁中，棱AB＝BC＝3，棱BB₁＝4，连结B₁C，过B点作B₁C的垂线交CC₁于E，交B₁C于F.

(Ⅰ)求证A₁C⊥平面EBD；

(Ⅱ)求ED与平面A₁B₁C所成角的大小；

(Ⅲ)求棱锥C－BDE的体积.

22．（本小题满分14分）

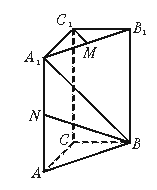
如图，直三棱柱ABC－A₁B₁C₁，底面△ABC中，CA=CB=1，∠BCA=90°，棱AA₁=2，M、N分别是A₁B₁、A₁A的中点.

（1）求的长；

（2）求cos<>的值；

（3）求证:A₁B⊥C₁M.

03-04年高三数学(文)全国统一标准测试(四)答案

一、1.D　2.D　3.C　4.C　5.B　6.A　7.B　8.D　9.D　10.B　11.D　12.B

二、13.13　14.或或　15.－α　16.

三、17.解：（1）=17,∴m+n=17　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2分

x²的系数为：

=m²－17m+136=(m－)²+63

∴m=8或m=9时，x²项的系数最小，最小值为64.　　　　　　　　　　　　　　　　　　　　　 6分

（2）当m=8时n=9;当m=9时n=8,∴a₅= =182　　　　　　　　　　　　　　　　　 8分

（3）f(x)=(1+x)⁸+(1+x)⁹

∴所有项的系数和为f(1)=2⁸+2⁹=768;　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　10分

又f(－1)=0,∴f(x)中所有x的指数是奇数的项的系数和为：

f(1)=384　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

18.解：（1）由展开过程可知，图2中A、B、C分别是边P₁P₃、P₁P₂、P₂P₃的中点，又P₁P₂=P₂P₃，故AB=AC.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2分

在图1中，取BC中点H，连AH、PH，

∵AH⊥BC，PH⊥BC，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 5分

∴BC⊥面PAH，即得PA⊥BC.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 7分

（2）由（1）知BC⊥面PAH，在图1中可知，PB=PC=AB=AC=13，BC=10，PH=HA=12，

S_△PAH=5，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　10分

∴V=S_△PAH·BC=.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

19.解：(1)1或2排在万位的五位数比32154小，有2=48个；　　　　　　　　　　 2分

3排在万位，1排在千位的五位数比32154小，共有=6个；　　　　　　　　　　　　4分

3、2、1依次排在前三位的有两个32145，32154；故有55个比32154小，所以32154是第56个.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

(2) 1排在万位的五位数有=24，故第20个数的万位必是1；　　　　　　　　　　　 8分

1排在万位，2、3、4分别排在千位的五位数共有3=18个；　　　　　　　　　　　 10分

因此第19个数为15234，第20个数为15243.　　　　　　　　　　　　　　　　　　　　　　　　　 12分

20.解：（1）设在半小时内甲能解决该问题是事件A，乙能解决该问题是事件B，那么两人都未解决该问题就是事件·，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　3分

由于两人是相互独立的求解的，我们得到

P（·）=P（）·P（）=［1－P（A）］［1－P（B）］=（1－）（1－）

=.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

(2)“问题得到解决”这一事件的概率为：

1－P（·）=1－=.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

21.解：(Ⅰ)连结AC，则AC⊥BD，又AC是A₁C在平面ABCD内的射影

∴A₁C⊥BD；

又∵A₁B₁⊥面B₁C₁CB，且A₁C在平面B₁C₁CB内的射影B₁C⊥BE，

∴A₁C⊥BE，又∵BD∩BE=B∴A₁C⊥面EBD.　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分

(Ⅱ)连结DF，A₁D，∵EF⊥B₁C，EF⊥A₁C，

∴EF⊥面A₁B₁C，

∴∠EDF即为ED与平面A₁B₁C所成的角.　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

由条件AB=BC=3，BB₁=4，可知B₁C=5，BF=，B₁F=，CF=，EF=·BF

=，EC=·BB₁=

∴ED=

∴sinEDF=，

∴ED与平面A₁B₁C所成角为arcsin　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　9分

（Ⅲ）V_{棱锥C－BDE}=V_锥E－BCD=S_△BCD·EC=××3×3×=.　　　　　　　　 12分

22.解：（1）以C为原点CA所在直线为x轴，CB所在直线为y轴，CC₁所在直线为z轴，建立空间直角坐标系O－xyz. 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2分

则B(0，1，0)，N(1,0,1)，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分

可求得=；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

（2）由A₁（1，0，2）、B(0，1，0)、C(0，0，0)、B₁(0，1，2)，

得=（1，－1，2）， =（0，1，2），　　　　　　　　　　　　　　　　　　　　　　　　　　　　8分

从而得cos<>=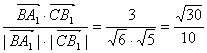；　　　　　　　　　　　　　10分

（3）又C₁(0，0，2)、M(0.5，0.5，2),

得=（－1，1，－2）， =（0.5，0.5，0）　　　　　　　　　　　　　　　　　　　　12分

所以·=－0.5+0.5+0=0,

所以⊥.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 14分