绝密 ★ 启用前
03-04年高三数学(理)全国统一标准测试(一)
命题范围：第一章 集合与简易逻辑，第二章 函数，第三章 数列，第四章 三角函数
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分.共150分，考试时间120分钟.
第Ⅰ卷(选择题 共60分)
注意事项：
1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案.不能答在试题卷上.
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1.函数f(x)=sin
x+cos(x+1)的图象相邻的两条对称轴间的距离是
A.3π B.
C.
D.
2.命题p:如果x2+2x+1－a2<0,那么－1+a<x<－1－a.
命题q:a<1.那么，q是p的（ ）条件.
A.必要不充分 B.充分不必要
C.充要 D.既不充分也不必要
3.要得到函数y=3f(2x+
)的图象，只须将函数y=3f(2x)的图象
A.向左平移个单位 B.向右平移
个单位
C.向左平移个单位 D.向左平移
个单位
4.集合{1，2，3}的子集的个数为
A.7 B.9
C.8 D.5
5.数列{an}中，an≠0,前n项和Sn=pn2+qn(p,q为非零实数），若m>1且有以下两式成立：am－1－am2+am+1=0,a1+a2+…+a2m－1=38.则m的值是
A.38 B.20
C.19 D.10
6.设α，β是第二象限的角，且sinα<sinβ，则下列不等式成立的是
A.tanα<tanβ B.cotα>cotβ
C.cosα<cosβ D.secα<secβ
7.关于x的函数y=log
(a2－ax+2a)在［1，+∞
上为减函数，则实数a的取值范围是
A.（－∞,0） B.(－1,0)
C.(0,2
D.(－∞,－1)
8.若f(x)是偶函数，且当x∈［0,+∞时，f(x)=x－1,则不等式f(x－1)>1的解集是
A.{x－1<x<3} B.{xx<－1,或x>3}
C.{xx>2} D.{xx>3}
9.今有一组实验数据如下：
| T | 1.99 | 3.0 | 4.0 | 5.1 | 6.12 |
| v | 1.5 | 4.04 | 7.5 | 12 | 18.01 |
现准备用下列函数中的一个近似的表示这些数据满足的规律，其中最接近的一个是
A.v=log2t B.v=logt
C.v=
D.v=2t－2
10.已知函数f(x)=x2,集合A={xf(x+1)=ax,x∈R},A≠
且A∪R+=R+，则实数a的取值范围是
A.（0，+∞） B.(2,＋∞)
C.［4,+∞ D.(－∞,0)∪［4,+∞)
11.等比数列{an}中，已知a1+a2+a3+a4=10,a5+a6+a7+a8=－5,则数列{an}的前16项和S16为
A.－50 B.
C.
D.－
12.下列判断错误的是
A.命题“若q则p”与“若
p则q”是互为逆否命题
B.“am2<bm2”是“a<b”的充分必要条件
C.“矩形的两条对角线相等”的否命题为假
D.“命题
{1,2}或4
{2,3}”为真
绝密 ★ 启用前 (十月号)
全国统一标准测试
数 学（理工农医类）
第Ⅱ卷 (非选择题 共90分)
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中的横线上.
13.已知α为第二象限角，且cos
,则cot
的值是__________.
14.若y=loga(ax2－4ax+3)的值域为全体实数集R，则a的取值范围为__________.
15.设f(x)是定义域为R最小正周期为π的周期函数，而且f(x)在［
］上是增函数，试写出f(x)的一个解析式：__________.
16.给出以下结论：
①通项公式为an=a1()n－1的数列一定是以a1为首项，为公比的等比数列；
②存在角α使得tanα+cotα=－
成立；
③函数y=
在定义域上是单调递减的；
④若α，β∈(
,π)，且tanα<cotβ，则α+β<;
⑤函数y=log(4－x2)的值域是［－2，+∞).
其中可能成立的结论的序号是__________.（注：把你认为正确的命题的序号都填上）
三、解答题：本大题共6小题，共74分.解答过程应写出文字说明、证明过程或演算步骤.
17.（本小题满分12分）
设sinx+
cosx+a=0在［0，］内有且只有两个x的值x1和x2使等式成立.
（1）求常数a的取值范围；
（2）求x1+x2的值.
18.（本小题满分12分）
已知命题p:{x1－
≤2,x∈R},和命题q:{xx2－2x+1－m2>0,m<0,x∈R},若非p是q的充分非必要条件，求实数m的取值范围.
19.（本小题满分12分）
已知数列{an}的前n项和Sn=n2;设bn=
,记数列{bn}的前n项和为Tn.
(1)求数列{an}的通项公式；
(2)证明：Tn<1.
20.(本小题满分12分)
我国是水资源比较贫乏的国家之一，各地采用价格调控等手段来达到节约用水的目的.某市用水收费的方法是：水费=基本费+超额费+损耗费.
若每户用量不超过最低限量a(m3)时，只付基本费8元和每户每月的定额损耗费c元；若用水量超过a(m3)时，除了付同上的基本费和损耗费外，超过部分每1 m3付b元的超额费.已知每户每月的定额损耗费不超过5元.
该市一家庭今年第一季度的用水量和支付费用如下表所示：
| 月 份 | 用水量（m3） | 水费（元） |
| 1 | 9 | 9 |
| 2 | 15 | 19 |
| 3 | 22 | 33 |
（1）请根据上表中的数据，求a,b,c的值；
（2）写出某户在一个月中的水费y元与在这个月中的用水量x(m3)的函数关系式.
21.(本小题满分12分）
已知数列{an}中，a1=14,a2=2,且满足an+2－2an+1+an=0(n∈N*)
(1)求数列{an}的通项公式；
(2)设Sn=a1+a2+…+an,求Sn;
(3)设bn=
,Tn=b1+b2+…+bn.是否存在最大整数m,使得任意n∈N*,均有Tn>
.
22.(本小题满分14分）
已知f(x)是定义在［－1，1］上的奇函数，且f(1)=1,若a,b∈［－1,1］,a+b≠0时，有
＞0.
(1)判断函数f(x)在［－1，1］上是增函数，还是减函数，并证明你的结论；
（2）解不等式：f(x+)＜f(
);
(3)若f(x)≤m2－2pm+1对所有x∈［－1,1］,p∈［－1,1］(p是常数）恒成立，求实数m的取值范围.
03-04年高三数学(理)全国统一标准测试(一)答案
一、1.B 2.A 3.C 4.C 5.D 6.D 7.B 8.B 9.C 10.C 11.B 12.C
二、13.
14.［,1)∪(1,+∞)
15.y=－cos(2x－
)(答案不惟一，只要符合题意均给满分）
16.④⑤
三、17.解：（1）由条件得－
=sin(x+). 3分
∵0≤x≤,∴≤x+≤
. 6分
结合函数y=－和y=sin(x+)的图象，易知
≤－<1.
∴－2<a≤－就是所求. 9分
（2）∵x∈［0, ］,∴当－2<a≤－时，函数图象关于直线x=
对称，故x1+x2=.
12分
18.解：由1－≤2得－2≤x≤10 2分
非p:A={xx>10或x<－2} 4分
因m<0,由x2－2x+1－m2>0(m<0)得
命题q:B={xx<1+m或x>1－m} 7分
又因为非p是q的充分非必要条件，所以AB 9分
所以
,得－3≤m<0. 12分
19.（1）解：a1=S1=1;
当n≥2时，有an=Sn－Sn－1=n2－(n－1)2=2n－1 ①
而a1=1也适合①式，故数列{an}的通项公式为an=2n－1. 5分
（2）证明：Tn=
,由错位相减法得
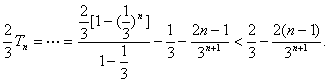10分
∴Tn＜1－
＜1.(亦可用数学归纳法证明)
12分
20.解：（1）若a<9,根据题中所给表得：
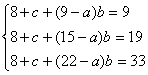2分
前两个式子相减得b=
,后两个式子相减得b=2,相互矛盾，故a<9不可能. 4分
若9≤a<15,根据题中所给表得：
解得
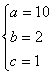8分
若15≤a<22,根据题中所给表得：
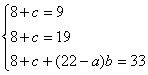无解.
若a≥22,根据题中所给表得：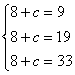
无解.
综合以上得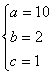. 10分
|
12分
21.解：（1）由已知得an+2－an+1=an+1－an(n∈N*),故{an}为首项14，公差为－12的等差数列，an=26－12n. 2分
（2）S1=14；S2=16；当n≥3时，Sn=a1+a2－(a3+a4+…+an)=16－
=6n2－20n+32 7分
(3)因数列{bn}各项为正，所以Tn是递增的，要使得对任意n∈N*,均有Tn＞成立，只需T1＞即可，由此得m＜8.故存在最大整数m=7,使得任意n∈N*,均有Tn>成立. 12分
22.解：（1）函数f(x)在［－1，1］上是增函数.
证明：设任意x1,x2∈［－1,1］,且x1<x2.
由于f(x)是定义在［－1，1］上的奇函数，
∴f(x2)－f(x1)=f(x2)+f(－x1). 2分
因为x1<x2,所以x2+(－x1)≠0,由已知有
＞0,
∵x2+(－x1)=x2－x1>0
∴f(x2)+f(－x1)>0,
即f(x2)>f(x1),
所以函数f(x)在［－1，1］上是增函数. 5分
（2）由不等式f(x+）＜f()得
,
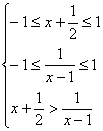解得－1<x<0,即为所求. 10分
（3）由以上知f(x)最大值为f(1)=1,所以要f(x)≤m2－2pm+1对所有x∈［－1,1］,p∈ ［－1,1］(p是常数)恒成立，只需1≤m2－2pm+1恒成立，得实数m的取值范围为m≤0或m≥2p. 14分