高三数学(理)全国统一标准测试(四)

绝密 ★ 启用前　　　　　　　　　　　　　　　　　　　　　　　　　　 (一月号)

03-04年高三数学(理)全国统一标准测试(四)

命题范围：第九章　直线、平面、简单几何体　第十章　排列、组合与概率

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷（非选择题）两部分.

第Ⅰ卷(选择题  共60分)

注意事项：

1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.

2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案.

3.如果不采用答题卡答题，请把第Ⅰ卷（选择题）的答案填入第Ⅱ卷的选择题答题表中.

参考公式：

sinαcosβ=［sin(α+β)+sin(α－β)］　　

cosαsinβ=［sin(α+β)－sin(α－β)］

cosαcosβ=［cos(α+β)+cos(α－β)］

sinαsinβ=－［cos(α+β)－cos(α－β)］

sinα+sinβ=2sincos

sinα－sinβ=2cossin

cosα+cosβ=2coscos

cosα－cosβ=－2sinsin

S_台侧= (c′+c)l(c、c分别表示上、下底面周长，l表示斜高或母线长)

V_台体=（S′++S)h(S′、S分别表示上、下底面积，h表示高）

一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.设正四棱锥底面边长为3，体积为，则它的侧面与底面所成角的大小为

A.75°　　　　　　　  B.30°　　　　　　　  C.45°　　　　　　　  D.60°

2.由正方体的八个顶点中的四个顶点所组成的正四面体的表面积与正方体的表面积比是

A.　　　　　　　　 B.　　　　　　　　　　　　　 C.　　　　　　　　 D.

3.设m=3⁷+·3⁵+·3³+·3,n=·3⁶+·3⁴+·3²,则m－n等于

A.0　　　　　　　　　　　　　　　B.127　　　　　　　　　　　　　　　　　　　　 C.128　　　　　　　　　　　　　 D.129

4.设a、b、c表示三条直线，α、β表示两个平面，则下列命题中逆命题不成立的是

A.c⊥α,若c⊥β,则α∥β

B.bβ,c是a在β内射影，若b⊥c,则a⊥b

C.bβ,若b⊥α,则β⊥α

D.bα,cα,若c∥α,则b∥c

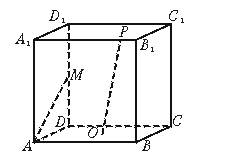5.正方体ABCD—A₁B₁C₁D₁中，E、F分别是AA₁和AB的中点，则EF与对角面A₁C₁CA所成角为

A.30°　　　　　　　　　　　　　　　　　　　　　　　　　　　 

B.45°

C.60°　　　　　 　　　　　　　　　　　　　　　　　　 

D.90°

6．把英语单词“error”中字母的拼写顺序写错了，则可能出现的错误种数是

A.20　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.19

C.10　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.9

7.在有太阳的时候，一个大球放在地面上，球的影子伸到距球与地面的接触点10米处，同一时刻，一根长1米，一端接触地面而垂直于地面的尺子的影子长度是2米，则球的半径是

A.2.5米　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.10－20米

C.6－米　　　　　　　　　　　　　　　　　　　　　　　　　D.9－4米

8.设集合M={－1，0，1}，N={2，3，4，5，6}，映射f:M→N,使对任何x∈M,都有x+f(x)+xf(x)是奇数，这样的映射f的个数为

A.122　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.15

C.50　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.27

9.对于不共面的三个向量a、b、c，下列命题正确的是

A.(a·b)²·c=(a²·b²)·c

B.总可以找到两个实数λ、μ,使c=λa+μb

C.这三个向量不能相加

D.对空间任意向量d,存在有序实数组x₁、x₂、x₃、x₄,使x₁d=x₂a+x₃b+x₄c,其中x₁不等于零

10.如图①是一个正三棱柱形容器，底面边长为a,高为2a,内装水若干.将容器放倒，把一个侧面作为底面，如图②，这时水面恰好为中截面.请问图①中容器内水面的高度是

 

图①　　　　　　　　　　　 图②

A.a　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　 B. a

C. a　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D. a

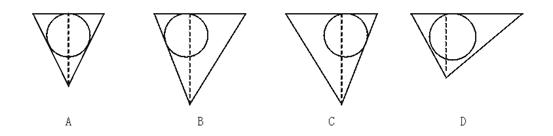
11.如图，在一个倒置的正三棱锥容器中，放入一个钢球，钢球恰与棱锥的四个面都接触上，经过棱锥的一条侧棱和高作截面，正确的截面图形是

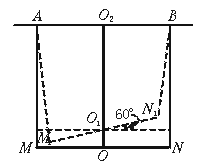
12.如图在水平横梁上A、B两点处各挂长为50 cm的细绳AM、BN，在MN处栓长为60 cm的木条，MN平行于横梁，木条绕过MN中点O的铅垂线旋转60°，则木条比原来升高了

A.10 cm　　　　　　　　

B.5 cm

C.10 cm　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.5cm

第Ⅱ卷 (非选择题  共90分)

二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中的横线上）

13.已知甲烷的分子结构是：中心为一个碳原子，外围有4个氢原子（这4个氢原子构成一个正四面体的四个顶点）.设中心碳原子到外围4个氢原子连成的四条线段两两组成的角为θ，则cosθ=_________.

14.甲射击命中目标的概率是，乙射击命中目标的概率是，丙射击命中目标的概率是，现在三人同时射击目标，则目标被击中的概率为_________.

15.降水量是指水平面上单位面积所降雨水的深度，用上口直径为38厘米，底面直径为24厘米，深为35厘米的圆台形水桶来测量降水量.如果在一次降水过程中，用此桶接得的雨水正好是桶深的，则此次下雨的降水量为_________毫米.

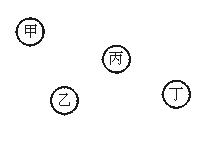
16.如图，甲、乙、丙、丁为湖中四个亭子，要建3座小桥将四个亭子连接起来，不同的建桥方案共有_________种.

三、解答题(本大题共6小题，共74分.解答过程应写出文字说明、证明过程或演算步骤)

17．（本小题满分12分）

已知整式函数f(x)=(1+x)^m+(1+x)ⁿ(m,n∈N^*)的展开式为f(x)=a₀+a₁x+a₂x²+a₃x³+…+a_mx^m,已知a₁=17.

 (1)求f(x)中x²项系数的最小值；

（2）求a₅;

(3)求f(x)中所有x的指数是奇数的项的系数和.

18.（本小题满分12分）

从三棱锥P—ABC（如图1）的顶点沿着三条侧棱PA、PB、PC剪开，成平面图形，得到△P₁P₂P₃（如图2），且P₁P₂=P₂P₃；

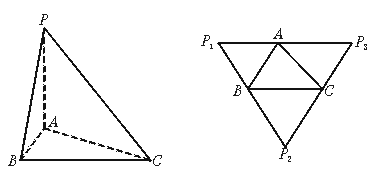
图1　　　　　　　　　　　　 图2

（1）在棱锥P—ABC中，求证：PA⊥BC；

（2）P₁P₂=26，P₁P₃=20，求三棱锥的体积.

19.（本小题满分12分）

已知集合P={mm=2k,k∈N,k≤6},Q={nn=6k,k∈N,k≤6}

(1)若集合A含有三个元素，且AP,这样的集合A有多少个？所有集合A中元素之和是多少？

（2）若集合A、B各含有三个元素，且AP,BQ,A∩B=,这样的集合A、B有多少对？

20.（本小题满分12分）

袋中有12个球，其中白球4个，甲、乙、丙三人接连从袋中取球，甲先取，然后乙，然后丙，然后甲，…如此进行下去，规定先取出一个白球者获胜，分两种：（1）抽后放回；（2）抽后不放回.

则甲乙丙获胜的概率各为多少？

21.（本小题满分12分）

如图，已知三棱柱ABC—A₁B₁C₁中，底面△ABC是等腰直角三角形，且∠BAC=

Rt∠,BC=2a,侧棱AA₁与AB、AC所成角都是60°,且底面△ABC的面积是截面△A₁BC面积的倍.

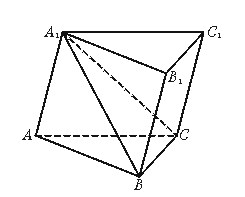
求：（1）A₁A与底面ABC所成的角；

（2）二面角A—BC—A₁的大小；

（3）这个三棱柱的侧面积.

22.（本小题满分14分）

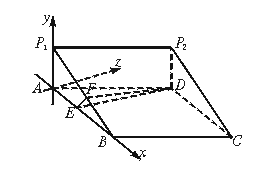
如图一楔体，ABCD是边长为2的菱形，∠BAD=60°,P₁A⊥面ABCD，P₂D⊥面ABCD，P₁A=P₂D=，求：

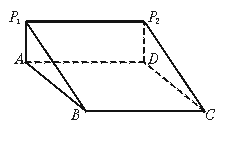
（1）二面角A—P₁B—D的大小；

（2）异面直线P₁D与P₂B所成角的大小.

03-04年高三数学(理)全国统一标准测试(四)答案

 一、1.D　2.B　3.D　4.C　5.A　6.B　7.B　8.C　9.D　10.C　11.B　12.A

二、13.－　14.　15.2.2　16.16

三、17.解：（1）=17,∴m+n=17　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2分

x²的系数为：

=m²－17m+136=(m－)²+63

∴m=8或m=9时，x²项的系数最小，最小值为64.　　　　　　　　　　　　　　　　　　　　　 6分

（2）当m=8时n=9;当m=9时n=8,∴a₅= =182　　　　　　　　　　　　　　　　　 8分

（3）f(x)=(1+x)⁸+(1+x)⁹

∴所有项的系数和为f(1)=2⁸+2⁹=768;　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　10分

又f(－1)=0,∴f(x)中所有x的指数是奇数的项的系数和为：

f(1)=384　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

18.解：（1）由展开过程可知，图2中A、B、C分别是边P₁P₃、P₁P₂、P₂P₃的中点，又P₁P₂=P₂P₃，故AB=AC.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2分

在图1中，取BC中点H，连AH、PH，

∵AH⊥BC，PH⊥BC，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 5分

∴BC⊥面PAH，即得PA⊥BC.　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　7分

（2）由（1）知BC⊥面PAH，在图1中可知，PB=PC=AB=AC=13，BC=10，PH=HA=12，

S_△PAH=5，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　10分

∴V=S_△PAH·BC=.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

19.解：（1）P={2，4，6，8，10，12}

A有=20个.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2分

在20个集合中含有元素2的有： =10个；

含有其他（即4，6，8，10，12）各元素的均各有10个；　　　　　　　　　　　　　　　 5分

故所有A中各元素之和为（2+4+6+8+10+12）×10=420.　　　　　　　　　　　　　　　　　6分

（2）Q={6，12，18，24，30，36}，符合条件的A、B有三类：

①6，12A时，有对；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

②6A,12∈A或12A,6∈A时，则有2对；　　　　　　　　　　　　　　　　　　　　　10分

③16，12∈A时，则有对，

故符合条件的A、B对共有： =216.　　　　　　　　　　　　　 12分

20.解：（1）抽后放回，是独立试验，每抽到白球的概率为，则

甲获胜的概率为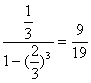： +…=；　　　　　　　 2分

乙获胜的概率为：（）·（）+（）⁴·（）+（）⁷·（）+…

=；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分

丙获胜的概率为：1－.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

（2）抽后不放回.

甲获胜的概率为：

=.　　　　8分

乙获胜的概率为：

=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　10分

丙获胜的概率为：1－.　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

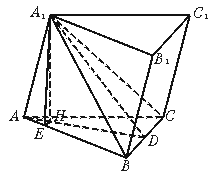
21.解：（1）作A₁H垂直于平面ABC于H，因

∠A₁AB=∠A₁AC=60°,所以H在∠BAC的角平分线上. 　2分

连AH并延长交BC于D，所以∠A₁AH就是A₁A与底面ABC所成的角.3分

作A₁E⊥AB于E，连接EH，设A₁A=x,在直角三角形A₁AE中，得AE=x,在等腰直角三角形AEH中，得AH=x,在直角三角形A₁HA中，得cosA₁AD=,

∴A₁A与底面ABC所成的角为45°.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

（2）因AB=AC=a,所以△A₁AB≌△A₁AC，所以A₁B=A₁C，则AD⊥BC，连A₁D，则A₁D⊥BC，所以∠A₁DA是二面角A—BC—A₁的平面角.　　　　　　　　　　　　　　　　　　 8分

由∠A₁AD=45°,又因S_△ABC=，所以AD=A₁D=a,

∴∠A₁DA=45°,即二面角A—BC—A₁为45°.　　　　　　　　　　　　　　　　　　　　　　　　　　　　10分

（3）由（2）得A₁A⊥BC，所以BB₁⊥BC，所以BCC₁B₁为矩形.

由于AD=a,AA₁=a,AB=a.

所以S_侧=2=2·a·a·+2a·a=()a².12分

22.解：（1）取AB的中点E，连接DE，则DE⊥AB，DE⊥面ABP₁，作EF垂直于P₁B于F，连接DF，∴DF⊥P₁B，∠DFE为二面角A—P₁B—D的平面角.　　　　　 4分

∵DE=2·=，EF=·.

在△DEF中，tanDFE=,

∴∠DFE=arctan

∴二面角A—P₁B—D的大小为arctan.　　　　　　　　　　　　　　　　　　　　　　　　　　　 7分

（2）以A为原点，分别以AB、AP₁所在直线为x轴和y轴,过A点且与平面ABP₁垂直的直线为z轴，建立空间直角坐标系A—xyz

则B（2，0，0），P₁（0，，0），D（1，0，），P₂（1，，）10分

则=(1,－，）， =（1，－，－）

=，=，·=1+3－3=1　　　　　　　　　　　　　　　　　　　　　12分

∴cos＜,＞=

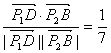
∴<>=arccos

∴异面直线P₁D与P₂B所成角的大小为arccos　　　　　　　　　　　　　　　　　　　　　　 　14分