福建福州02-03年高三数学模拟(一)
说明：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分.考试时间120分钟.
参考公式：
三角函数的积化和差公式
sinαcosβ=
［sin(α+β)+sin(α－β)］
cosαsinβ=［sin(α+β)－sin(α－β)］
cosαcosβ=［cos(α+β)+cos(α－β)］
sinαsinβ=－［cos(α+β)－cos(α－β)］
正棱台、圆台的侧面积公式
S台侧=(c′+c)l
其中c′、c分别表示上、下底面周长，l表示斜高或母线长球的体积公式
V球=
πR3
其中R表示球的半径.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的)
1.设Z=3+i,那么
等于
A.3+i
B.3－i
C.
i+
D.+i
2.函数y=x+
的图象关于（ ）对称
A.x轴 B.y轴 C.原点 D.直线y=x
3.(理)已知m、n是两条不重合的直线，α是平面，给出以下命题：
|
|
①
n⊥α ②
m∥n
| |||
| |||
③
n∥α ④
n⊥α
其中，正确命题的个数为
A.1 B.2 C.3 D.4
（文）抛物线y=4x2的焦点坐标是
A.（1，0） B.（0，1） C.（0，2）
D.（0，
）
4.不等式x｜x｜＜x的解集为
A.｛x｜0＜x＜
B.｛x｜－1＜x＜
C.｛x｜0＜x＜1或x＜－
D.｛x｜－1＜x＜0或x＞
5.（理）函数y=－2sin(4x+
)的图象与x轴的交点中，离原点最近的一点是
A.（－
,0） B.(,0)
C.(
,0)
D.(－,0)
（文）函数y=x2+3(x≤－1)的反函数是
A.y=
(x≥3) B.y=－(x≥3)
C.y=－(x≥4)
D.y=(x≥4)
6.(理)一个圆柱的轴截面是正方形，其侧面积与一个球的表面积相等，那么这个圆柱的体积与这个球的体积之比为
A.3∶2
B.1∶1
C.2∶3
D.
∶
（文）已知（x－
）7展开式的第4项等于5，则x等于
A.
B.－
C.7
D.－7
7.函数y=
+arcsin2x的反函数是
A.y=sinx x∈［0,π］
B.y=cosx x∈［0,π］
C.y=－sinx x∈［0,π］
D.y=－cosx x∈［0,π］
|
8.（理）已知曲线C：
(θ为参数)，直线l经过点（0，），倾斜角为α，则α=
是直线l与曲线C相切的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也非必要条件
（文）F1、F2分别是椭圆
+
=1(a＞b＞0)的左、右焦点，P是椭圆短轴的一个端点，若△F1PF2是等腰直角三角形，其面积为1，则a的值是
A.1
B.
C.2
D.4
9.（理）某年段接收转校生5人，准备安排到（1）、（2）、（3）、（4）四个班，每班至少安排1人，不同的安排方案共有（ ）种
A.625 B.480 C.240 D.96
（文）设数集M=｛x｜0≤x≤
｝,N=｛x｜
≤x≤1｝，如果把b－a叫做集合｛x｜a≤x≤b｝的“长度”，那么集合M∩N的“长度”是
A.
B.
C.
D.
10.（理）已知a+b＞0,b=4a,(a+b)n展开式按a的降幂排列，其中第n项与第n－1项相等，那么正整数n等于
A.4 B.9 C.10 D.11
（文）若数列｛an｝是公比的绝对值小于1的无穷等比数列，且a1+a2+a3=
,a1·a2·a3=
,则此数列所有项之和为
A.
B.－
C.
D.1
11.（理）已知
(1+
)n=e(e为常数)，则（1+
）n等于
A.1 B.e C.
D.e3
（文）某市新城区的居民住宅面积总量每年比上一年增长10.4%，那么经过x年（x∈N）可以增长到原来的y倍，则函数y=f(x)的图象大致为下列图象中
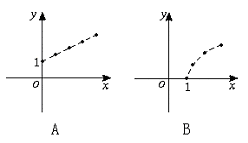
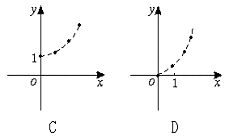
12.（理）设数集M=｛x｜m≤x≤m+｝,N=｛x｜n－≤x≤n｝，且M、N都是集合｛x｜0≤x≤1｝的子集，如果把b－a叫做集合｛x｜a≤x≤b｝的“长度”，那么集合M∩N的“长度”的最小值是
A.
B.
C.
D.
（文）对于定义在实数集R上的函数f(x)，如果存在实数x0，使f(x0)=x0,那么x0叫做函数f(x)的一个不动点.已知函数f(x)=x2+2ax+1不存在不动点，那么a的取值范围是
A.（－，
） B.（－，）
C.（－1，1） D.（－∞,－1）∪(1,+∞)
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题，每小题4分，共16分.把答案填在题中横线上)
13.(理)已知双曲线
－
=1的离心率e=
,则实数m的值是_____________.
（文）不等式x｜x｜＜x的解集是_____________.
14.(理)已知圆锥的母线长为1，并且有3条母线两两垂直，则该圆锥的高为____________.
（文）某年段接收转校生4人，准备安排在（1）、（2）、（3）三个班，每班至少安排1人，不同的安排方案共有_____________种.(用数字作答)
15.（理）对于定义在实数集R上的函数f(x)，如果存在实数x0，使f(x0)=x0，那么x0叫做函数f(x)的一个不动点.已知函数f(x)=x2+2ax+1不存在不动点，那么实数a的取值范围是_____________.
（文）直线x－3y－6=0绕它与y轴的交点，按逆时针方向旋转
,所得的直线方程是________________________.
16.(理)某地一种出租车的车费的计算规定如下：基本车费为7元，行程不足3公里时，只收取基本车费；行程不足5公里时，大于等于3公里的那部分，每增加0.5公里，加收车费0.7元，不足0.5公里按0.5公里计算（如：行程为x公里，在4≤x＜4.5时，车费为7+0.7×3=9.1元)；行程大于等于5公里时，大于等于5公里的那部分，每增加0.2公里，加收车费0.4元.如果某人从A地到B地，共付车费11元，那么从A地到B地的行程x的范围是_______________________.
（文）关于x的函数f(x)=cos(x+
)有以下命题：
①对任意常数，f(x)都是非奇非偶函数；
②不存在常数，使f(x)既是奇函数，又是偶函数；
③存在常数，使f(x)是偶函数；
④对任意常数，f(x)都不是奇函数
其中，假命题的序号是_________________________.
三、解答题(本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
(理)已知f(x)=
(1)求f(x)的定义域、值域；
(2)若f(x)=2,－＜x＜
，求x的值.
（文）已知f(x)=sin2x+3cos2x(x∈R).
(1)求f(x)的最小正周期；
(2)当x为何值时，f(x)取得最大值，最大值是多少？
(3)求f(x)的单调递减区间.
18.(本小题满分12分)
斜三棱柱ABC－A1B1C1中，侧面AA1C1C⊥底面ABC.
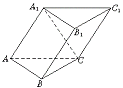∠ABC=90°,BC=2,AC=2,AA1⊥A1C,AA1=A1C.
(1)求侧棱AA1与底面ABC所成角的大小；
(2)求侧面AA1B1B与底面ABC所成二面角的大小；
(3)求点C到侧面AA1B1B的距离.
19.(本小题满分12分)
数列｛an｝的前n项和Sn=n2－2n(n∈N),数列｛bn｝满足bn=
(n∈N).
(理)(1)判断数列｛an｝是否为等差数列，并证明你的结论；
(2)求数列｛bn｝中值最大的项和值最小的项.
（文）（1）求数列｛an｝的通项公式；
（2）求［bn(bn－2)］的值.
20.(本小题满分12分)
某企业生产的新产品必须先靠广告来打开销路.该产品的广告效应是产品的销售额与广告费之间的差.如果销售额与广告费的算术平方根成正比，根据市场抽样调查显示：每付出100元广告费，所得的销售额是1000元，问该企业应该投入多少广告费，才能获得最大的广告效应？是不是广告做得越多越好？
21.(本小题满分12分)
（理）已知抛物线C：y2=4(x－1)，椭圆C1的左焦点及左准线与抛物线C的焦点F和准线l分别重合.
(1)设B是椭圆C1短轴的一个端点，线段BF的中点为P，求点P的轨迹C2的方程；
(2)如果直线x+y=m与曲线C2相交于不同两点M、N，求m的取值范围.
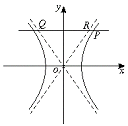
（文）过双曲线C：－=1(a＞0,b＞0)上任意一点P，作x轴的平行线，交双曲线的两条渐近线于Q、R两点.
求证：｜PQ｜·｜PR｜为定值.
22.(本小题满分14分)
(理)设函数f(x)是定义在R上的函数，对任意实数m、n,都有f(m)·f(n)=f(m+n),且当x＜0时，f(x)＞1.
（1）证明①f(0)=1；
②当x＞0时，0＜f(x)＜1;
③f(x)是R上的减函数；
（2）如果对任意实数x、y，有f(x2)·f(y2)≤f(axy)恒成立，求实数a的取值范围.
（文）已知函数f(x)=
(1)若a=，当x∈［1,+∞)时，求函数f(x)的最小值；
（2）当x∈［1,+∞］时，f(x)＞0恒成立，试求实数a的取值范围；
（3）当x∈［1,+∞)时，f(x)＞a恒成立，求实数a的取值范围.