高三数学月考试题(统编)

2003年高三数学月考试题(统编)

题 号	一	二	三						总 分
			17	18	19	20	21	22
得 分

本试卷满分150分，考试时间120分钟.

第Ⅰ卷（选择题，共60分）

得分 评卷人

一、选择题：（本大题共12小题，每小题5分，满分60分）

1．设A{1,2，3}，且A中至多有一个奇数，则这样的集合共有 （　　）

　　　 A．3个　　　　　　　　　　B．4个 　　　　　　　　 C．5个 　　　　　　　　　　D．6个

2．θ是第一象限角，那么恒有 　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　B．　　　 C．　　D．

3．已知a,b是异面直线，β是平面，且α⊥β，则　　　　　　　　　 　　　　　　　 （　　）

　　　 A．b与β相交 　　　　B．b与β不相交　　C．b与β不平行　　　　D． b与β不垂直

4．在三角形ABC中，已知角A>B>C，记m=sinAcosC，n=cosAsinC，p=simBcosB ，则

　 m、n、p的大小关系是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．m>n>p　　　　　　　　B．m>p>n 　　　　　　C．p>m>n　　　　　　　　 D．n>p>m

5．把函数，所得图象对应的函数是 　　　　　　　　　（　　）

　　　A．奇函数　　　　　　　　　　　　　　　　　　　　　　 B．偶函数　 　　　　　　

　　　 C．奇函数也是偶函数　　　　　　　　　　　　　　D．非奇非偶函数

6．将4个不同的小球放入两个盒子中，每个盒子至少放入一个小球，现求不同放法的种数。

　 甲列式子： 丁列式子：。其

　 中列式正确的是　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　 （　　）

　　A．甲 　　　　　　　　　　 B．乙 　　　　　　　　　 C．丙　　　　　　　　　　　　D．丁

7．设a,b∈R⁺，则下列不等式中一定不成立的是　　　　　　　　  　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　　

　　　 C．　　　　　　　　　　　　　　　　D．

8．设x,y∈R，则使x+y>1成立的充分不必要条件是　　　　　　  　　　　　　　　　　（　　）

　　

9．圆轴交于A，B两点从圆心看这两点的视角为直角，

　 则c=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　（　　）

　　　 A． 8 　　　　　　　　　　 B． 3 　　　　　　　　　 C．－3 　　　　　　　　　　  D．

10．过点P(1,1)且与双曲线有且仅有一个共点的直线共有　　 　　　　　　（　　）

　　　 A．1条　　　　　　　　　　B．2条　　　　　　　　　C．3条　　　　　　　　　　　D．4条

11．正项数列{a_n}中，若M=(a₁+a₂+…+a₁₉₈₉)·(a₂+a₃+…+a₁₉₉₀)，N=(a₁+a₂+…+a₁₉₉₀)·

　　(a₂+a₃+…+a₁₉₈₉)，则M，N的大小关系为　　　　　　　　　　　　　　　  　　　 （　　）

　　　 A．M>N 　　　　　　　　 B．M=N　　　　　　　　 C．M<N　　　　　　　　　　D．M、N无大小关系

12．如图，把长方体的火柴盒外壳沿棱AA₁压平，将压平的火柴盒切开分成两部分，然后还

　　原成长方体。则还原后的切口的形状可能是　　　　　　　　　　　  (　　 )

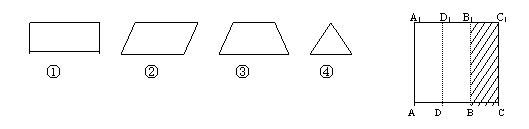　　　 A．①②④　　　　　　　 B．①②③　　　　　　　C．②③　　　　　　　　　　 D．②③④

第Ⅱ卷（非选择题，共90分）

得分 评卷人

　　　　　　　　　　  二、填空题：（本大题共4小题，每小题4分，满分16分）

13．ΔABC中，若4sinA+2cosB=1, 2sinB+4cosA=3,则∠A的大小为___________。

14．正n棱锥棱与底面所成的角为α，侧面与底面所成角为β，则tanα:tanβ=______________。

15．直线y=1-x交椭圆mx²+ny²=1于M，N两点，弦MN的中点为P，若K_OP=_________________。

16．银行计划将某资金给项目M投资一年，其余的60%资金给项目N，预计项目M有可

能获得19%到24%的年利润，N有可能获得29%到34%的年利润。年终银行必须回

笼资金，同时按一定的回扣率支付给储户。为了使银行的年纯利润不少于给M，N

总投资的10%而不大于总投资的15%，则给储户回扣率的最小值是　　　　　　　 。

三、解答题：（本大题6小题，共74分，解答应写出文字说明，证明过程或演算步骤）

得分 评卷人

　　

（本题满分12分）

17．已知函数f(x)=log_a(1-a^x)(其中a>0且a≠1)。

　 （Ⅰ）求f ^–1(x)，并指出其定义域；

　 （Ⅱ）解关于x的不等式log_a(1-a^x)>f ^–1(1).

　

得分 评卷人

　

（本题满分12分）

18．已知ΔABC的三个内角A、B．C成等差数列，其外接圆半径为1，且有

　　。

　 （Ⅰ）求A、B．C的大小；

　 （Ⅱ）求ΔABC的的面积。

得分 评卷人

　　

　　　　　　　　　　　　　  （本题满分12分）

19．如图，在三棱柱ABC-A₁B₁C₁中，A₁B₁是A₁C与B₁C₁的公垂线，

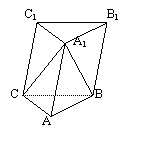AB=3cm，A₁A=AC=5cm，若直线A₁B与底面ABC所成的角

的大小为。

　 （Ⅰ）求证：平面A₁BC⊥平面ABC；

　 （Ⅱ）当为何值时，才能使二面角A₁-AC-B的正切值恰好

等于

　 （Ⅲ）在（Ⅱ）的条件下，求点C到平面A₁ABB₁的距离。

得分 评卷人

　 

　　　　　　　　　　　　  （本题满分12分）

20．甲、乙两网络公司，1996年的市场占有率均为A，根据市场分析的预测，甲公司第

n年(1996年为第1年)的市场占有率a_n=(n²-n+40)；

乙公司自1996年起逐年的市场占有率都有所增加，其

规律如图所示。

　 （1）分析图，求出乙公司第n年市场占有率的表达式。

　 （2）根据甲、乙两公司所在地的市场规律，如果某公司

　　　　的市场占有率不足另一公司市场占有率的20%，则

　　　　该公司将被另一公司兼并，经计算，2015年之前，不

　　　　会出现兼并局面，试问2015年是否会出现兼并局面，

并说明理由。

得分 评卷人

　　

　　　　　　　　　　　　 （本题满分12分）

21．数列{a_n},{b_n}满足a₁=1,a₂=r(r>0), b_n=a_n·a_n+1，且{b_n}是公比为q（q>0）的等比数列，设

　　c_n=a_2n-1+a_2n(n=1,2,3,…)，

　 （1）求{c_n}的通项公式；

　 （2）设{c_n}的前n项和为S_n,求；

　 （3）设

　　 

得分 评卷人

　　

　　　　　　　　　　　　 （本题满分14分）

22．设点P是双曲线C：上任一点，过P的直线与两渐近线分别交于

P₁、P₂，且，设O为坐标原点，ΔOP₁P₂的面积为27，求

双曲线方程.