北京市西城区2002年抽样测试
高三数学试卷（文科）
（2002.5）
参考公式：
三角函数的和差化积公式 球体的体积公式
其中R表示球的半径
一、选择题：本大题共12小题；每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合要求的。请选出正确答案。
1．已知集合
，
，则M∩N= （ ）
A. {xx≥1} B.{x x>1 } C.Φ D. {xx<0 或x>1}
2．已知
，
，则f(x)的图象 （ ）
A.与g(x)的图象相同
B.与g(x)的图象关于y的轴对称
C.是由g(x)的图象向左平移
个单位得到的
D.是由g(x)的图象向右平移个单位得到的
3．复数
的幅角主值是（ ）
A.
B. 
C.
D. 
4．已知直线
与直线
垂直，则a的值为 （ ）
A.2 B.-2 C.
D.
5．函数
的反函数是 （ ）
A.
B.
C.
D. 
6．某乒乓球队共有男女队员18人，现从中选出男女队员各一人组成一对双打组合由于在男队员中有两人主攻单打项目，不参与双打组合，这样一共有64种组合方式，则乒乓球队中男队员的人数为 ( )
A. 10人 B. 8人 C. 6人 D. 12人
7．一个圆柱的轴截面是正方形，其体积与一个球的体积之比为3:2。 则这个圆柱的侧面积与这个球的表面积之比为 ( )
A. 1:1 B.
C.
D.
3:2
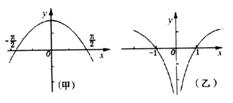
8．已知函数y=f(x)的图象如图甲所示，y=g(x)的图象如图乙所示。则函数
的图象可能是 ( )
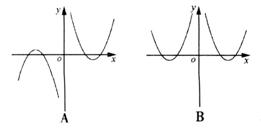
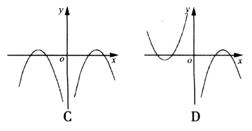
9．等差数列
是递减数列，且
，
，则数列的通项公式是（）
A.
B.
C.
D.
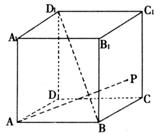
10．(如图) 正方体
中，点P在侧面
及其边界上运动，并且总是保持
，则动点P的轨迹是 ( )
Ａ.线段
Ｂ.线段
Ｃ.
中点与
中点连成的线段
D. BC 中点与
中点连成的线段
11．把长为12 厘米的细铁丝截成两段，各自围成一个正三角形，那么这两个正三角形面积之和的最小值是 ( )
Ａ.
B.
C.
D. 
12．对于抛物线
上任意一点Q, 点P(a,0)都满足PQ≥a，则a的取值范围是 （ ）
A. [0,1] B. (0,1) C. (-∞，1] D. (-∞，0)
二、填空题：本大题共4小题，每小题4分。共16分，把答案填在题中横线上。
13．在
的展开式中，常数项的值是__________________.(用数字作答)
14．不等式
的解集是____________。
15．已知抛物线
，当b(b∈R)变化时，抛物线顶点的轨迹方程为______.
16．G是正三角形ABC的中心，过G平行于BC的直线交AB于E，交AC于F，沿直线EF将三角形折成直二面角A-EF-C。则直线AC与平面EFCB所成的角为__________.
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。
17．（本小题满分12分）
已知函数
（a∈R, a是常数）,
（Ⅰ）求函数f(x)的最小正周期；
（Ⅱ）若f(x)的最大值为1，求a的值。
18．（本小题满分12分）
数列的前n项和
，其中b是常数。
(Ⅰ)若是等比数列，求b的值；
（Ⅱ）当是等比数列时，求
的值。
19．（本小题满分12分）
长方体中，AB=BC=1，
E是侧棱中点。
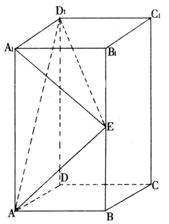
(Ⅰ)求证：直线AE⊥平面
；
(Ⅱ) 求三棱锥
的体积；
(Ⅲ) 求二面角
的平面角的正切值.
20．(本小题满分12分)
有一条生产流水线，由于改进了设备，预计第一年产量的增长率为150%，以后每年的增长率是前一年的一半，设原来的产量为a.
(Ⅰ)写出改进设备后的第一年，第二年，第三年的产量，并写出第n年与第n-1年（n≥2,n∈N）的产量之间的关系式；
(Ⅱ)由于设备不断老化，估计每年将损失年产量的10%，照这样下去，以后每年的产量是否始终是逐年提高？若是，请给予证明；若不是，请说明从第几年起，产量将比上一年减少。
21．（本小题满分13分）
设抛物线过定点A（0,2）且以x轴为准线。
（Ⅰ）试求抛物线顶点M的轨迹C的方程；
（Ⅱ）如果点P(a,1)不在线段y=1(-2≤x≤2)上，那么当a在什么范围内取值时，过P点存在一对互相垂直的直线同时与曲线C各有两个交点？
22．(本小题满分13分)
已知函数
（a, b, c∈R，a>0,b>0）是奇函数，当x>0时，f(x)有最小值2，其中b∈N且
.
(Ⅰ)试求函数f(x)的解析式；
(Ⅱ)问函数f(x)图象上是否存在关于点（1,0）对称的两点，若存在，求出点的坐标；若不存在，说明理由.
高三数学(文科)参考答案及评分标准
2002 .5
一、BCBDC AACDA BC
二、（13）-20 （14）
（15）
(16) 45°
三、解答题：其他解法仿此给分
17．解:(Ⅰ)
3分
6分
∴f（x）的最小正周期为2π。 8分
(Ⅱ)由（Ⅰ）可得f(x)的最大值为2+a 10分
∴2+a=1
∴a=-1 12分
18．解：（Ⅰ）由已知 
2分
当n≥2时,
5分
∴{
}从第二项起成等比数列.
若{}是等比数列，则首项为3，公比为2。
∴6+b=3 ∴b=-3 8分
（Ⅱ）由（Ⅰ） 
10分
∴
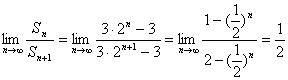12分
19. 解：（Ⅰ）已知几何体为长方体
∴
平面
∴
2分
又AB=1,
，E为的中点
∴△ABE为等腰直角三角形
∴
同理 
∴
为直角
即
∴AE⊥平面
4分
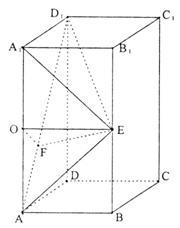
(Ⅱ) 由（Ⅰ）AE为三棱锥的高，
为Rt△
∴
6分
(Ⅲ) 取
中点O，连OE，则
、
∴EO⊥平面
过O在平面中作
，交
于F
连结EF，则
∴∠EOF为二面角的平面角
9分
在△AFO中，
∴
即二面角的平面角的正切值为
12分
(20) 解：
(Ⅰ)设第n年后的产量为,则
……
即 
,
, 
,
3分
∴
.
5分
(Ⅱ) 依题意
7分
由
,得
,
∴
10分
由于
。
又 n∈N ∴当n ≥5时,
。
故从第5年起产量比上一年减少。 12分
21．
解：（Ⅰ）设抛物线顶点M（x,y），y>0，则其焦点F(x,2y) 2分
∴
4分
化简得
∴抛物线顶点M的轨迹C的方程是
5分
（Ⅱ）设l, l′过（a,o）点互相垂直
由于当l, l′分别过（0，0），（0，2）点与C相交时，易知a=±1，不适合条件，而l, l′中一条与曲线C有两个交点，另一条线过（0，0）点与C相交时，由曲线的对称性知，仍满足题意，即l, l′与C各有两个交点
所以以下只考虑l,l′与椭圆全部各有两个交点的情况。6分
设l:y-1=k(x-a)
由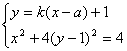
消y得
7分
∴
∴l与椭圆有两个不同交点的充要条件是
……①
同理，l与椭圆有两个不同交点的充要条件是
…………②
9分
解由①②组成的不等式组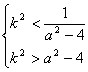
此不等式组有解的条件是
11分
解得
，又a>2
∴
∴
13分
22.解：(Ⅰ) ∵f(x)是奇函数，∴f(-x)=-f(x)
即 
∴bx+c= bx-c. ∴ c=0
2分
∵a>0，b>0
∴函数
4分
当且仅当，
时。等号成立
于是
∴
6分
由
得
即
∴
解得
又b∈N∴b=1 ∴a=1
∴
8分
（Ⅱ）设存在一点
在y=f(x)图象上，并且关于（1，0）的对称点
也在y=f(x)图象上， 9分
则
11分
消
得
∴
∴y=f(x)图象上存在两点
，
关于点（1，0）对称 13分