黄冈市2005年秋季高三年级期末考试
数 学 试 题(理科)
黄冈市教育科学研究院命制
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间为120分钟.
第Ⅰ卷(选择题 共60分)
一、 选择题(本大题共12小题,每小题5分,共60分,在每小题所给的四个选项中,只有一项是符合题目要求的)
1. 下列函数中,图象关于直线![]() 对称的是
对称的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设集合![]() ,则
,则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.给出两个命题:![]() 的充要条件是 为正实数;
的充要条件是 为正实数;![]() 存在反函数的函数一定是单调函数,则下列复合命题中真命题是
存在反函数的函数一定是单调函数,则下列复合命题中真命题是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知点![]() ,将线段
,将线段![]() 、
、![]() 各
各![]() 等分,设
等分,设![]() 上从左至右的第
上从左至右的第![]() 个分点为
个分点为![]() ,
,![]() 上从下至上的第
上从下至上的第![]() 个分点为
个分点为![]()
![]()
![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线为
轴的直线为![]() ,
,![]() 交
交![]() 于
于![]() ,则点
,则点![]() 在同一
在同一
A.圆上 B.椭圆上 C.双曲线上 D.抛物线上
5.已知 ![]() 是R上的单调增函数,则b的范围
是R上的单调增函数,则b的范围
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.由数字1,2,3,…,9组成的三位数中,各位数字按严格递增(如“156”)或严格递减(如“421”)顺序排列的数的个数是
A.120 B.168 C.204 D.216
7.原点![]() 在直线
在直线 ![]() 的两侧,则a的取值范围是
的两侧,则a的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若数列![]() 的通项公式为
的通项公式为![]() 的最大项为第x项,最小项为第y项,则
的最大项为第x项,最小项为第y项,则![]() 等于
等于
A.3 B.4 C.5 D.6
9.若圆 ![]() 至少能盖住函数
至少能盖住函数![]() 的一个最大值点和一个最小值点,则r的取值范围是
的一个最大值点和一个最小值点,则r的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对
10.设 ![]() 是函数
是函数![]() 的单调递增区间,将
的单调递增区间,将 ![]() 的图象按向量
的图象按向量![]() 平移得到一个新的函数
平移得到一个新的函数![]() 的图象,则
的图象,则![]() 的单调递减区间必定是
的单调递减区间必定是
A.![]() B.
B.![]() C.
C.
![]() D.
D.![]()
11.过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则
,则![]() 的值为
的值为
A.2 B.-2 C.
![]() D.
D.![]()
12.若直线![]() 交M、N两点,且M、N关于直线
交M、N两点,且M、N关于直线![]() 对称,动点
对称,动点![]() 在不等式组
在不等式组  表示的平面区域内部及边界上运动,则
表示的平面区域内部及边界上运动,则 ![]() 取值范围是
取值范围是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第Ⅱ卷(非选择题共90分)
二、填空题(本大题共4小题,共16分。把答案填在题中横线上)
13.若在![]() 的系数为-80,则a=
。
的系数为-80,则a=
。
14.若双曲线![]() 的一条准线恰为圆
的一条准线恰为圆![]() 的一条切线,则
的一条切线,则![]() 等于
。
等于
。
15.若一系列函数的解析式相同、值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为![]() 、值域为
、值域为![]() 的“同族函数”共有 个。
的“同族函数”共有 个。
16.设函数![]() 给出下列命题:
给出下列命题:
①![]() ②
②![]()
③![]()
上述三个命题中所有的正确命题的序号为 。
三、解答题
17.(本题满分12分)某学生语文、数学、英语三科考试成绩,在本次调研考试中排名全班第一的概率:语文为0.9,数学0.8,英语0.85,问这次考试中
(1)该生三科成绩均未获得第一名的概率是多少?
(2)该生恰有一科成绩未获得第一名的概率是多少?
18.(本题满分12分)已知向量![]()
![]()
![]()
![]() A,B,C是
A,B,C是![]() 的内角。
的内角。
(1)求角B的大小;
(2)求
![]() 的取值范围。
的取值范围。
19.(本题满分12分)(1)已知![]()
![]()
(2)设
![]() 若存在,求出点M的坐标,若不存在,请说明理由。
若存在,求出点M的坐标,若不存在,请说明理由。
20.(本题满分12分)若函数![]() 是周期为2的偶函数,当
是周期为2的偶函数,当![]() 时,
时,![]() ,在
,在![]() 的图象上有两点
的图象上有两点![]() 、
、![]() ,它们的纵坐标相等,横坐标都在区间
,它们的纵坐标相等,横坐标都在区间![]() 上,定点
上,定点![]() 的坐标为
的坐标为![]() (其中
(其中![]() ),求
),求![]() 面积的最大值。
面积的最大值。
21.(本题满分12分)已知数列![]() 的首项为
的首项为![]() ,前
,前![]() 项和为
项和为![]() ,且结任意的
,且结任意的![]()
![]() ,
,![]() 总是
总是![]() 与
与![]() 的等差中项。
的等差中项。
(1)求证:数列是![]() 等比例数项,并求通项
等比例数项,并求通项![]() ;
;
(2)证明:![]() 。
。
22.(本题满分14分)设![]() ,
,![]() ,常数
,常数![]() ,定义运算“
,定义运算“![]()
![]()
![]() ”,“
”,“![]()
![]()
![]()
![]() ”
”
(1)若![]() ,求动点
,求动点![]()
![]()
![]()
![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知直线![]() 与(1)中的轨迹
与(1)中的轨迹![]() 交于
交于![]() 两点,若
两点,若![]()
![]()
![]()
![]()
![]() ,试求
,试求![]() 的值;
的值;
(3)![]() 是平面上任意一点,定义
是平面上任意一点,定义
![]()
![]()
![]()
![]() ,
,
在轨迹![]() 上是否在两点
上是否在两点![]() ,使其满足
,使其满足![]() ,若存在,请求出
,若存在,请求出![]() 的取值范围,若不存在,请说明理由。
的取值范围,若不存在,请说明理由。
数学试题参考答案及评分标准(理科)
一、选择题(5分×12=60分)
1.B 2.B 3.D 4.D 5.D 6.B 7.C 8.A 9.B 10.D 11.D 12.C
二、填空题
13.-2 14.48 15.![]() 16.①②
16.①②
三、解答题
17.解:分别记该生语、数、英考试成绩排名全班第一的事件为![]() 、
、![]() 、
、![]() ,则
,则![]() ……………2分
……………2分![]()
![]()
![]()
![]()
![]()
![]()
![]()
答:该生三科成绩均未获得第一名的概率是0.003。 ……………6分
(2)![]()
![]()
![]()
![]()
![]()
![]()
![]() +
+![]()
![]()
![]() +
+![]()
![]()
![]()
![]()
答:该生司有一科成绩未获得第一名的概率是![]() ……………12分
……………12分
18.解:(1)![]() 与向量
与向量![]() 所成角为
所成角为![]() ,
, ![]()
![]()
![]() 或
或![]() (舍去)
(舍去)![]() ……………6分
……………6分
(2)由(1)可得![]()
![]() ……………8分
……………8分
![]() ……………10分
……………10分
![]()
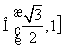 ,
,![]()
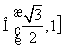
当且仅当![]() 时,
时, ![]() ……………12分
……………12分
19.(1)![]() ……2分
……2分
又![]()
![]()
![]()
![]()
![]() ……4分
……4分
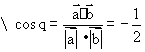 ……………5分
……………5分
![]() ……………6分
……………6分
(2)设存在点![]() ,且
,且![]()
![]()
![]() ……………8分
……………8分
![]() ,解得:
,解得:![]() 或
或![]() ……………10分
……………10分
![]() 或
或![]()
![]() 存在
存在![]() ,或
,或![]() 满足题意。
……………12分
满足题意。
……………12分
20.![]() 是以
是以![]() 为周期的周期函数,当
为周期的周期函数,当![]() 时,
时,![]() 当
当![]() 时,
时, ![]() ………3分
………3分
![]() 是偶函数
是偶函数 ![]() 当
当![]()
![]() 时,
时,![]() ,当
,当![]()
![]() 时,
时,![]() ………6分
………6分
设![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]()
![]()
![]() ,则
,则![]() ,
,![]() 的面积为
的面积为![]()
![]()
![]() ………9分
………9分
![]()
![]() 当
当![]() 时,
时,![]() 有最大值
有最大值 ![]() ……………12分
……………12分
21.(1)证:![]() 时,
时,![]() 即
即![]()
![]()
![]()
![]()
![]()
![]() ……………3分
……………3分
故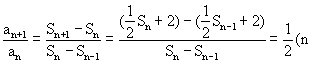
![]() ,又
,又![]()
![]() 数列
数列![]() 是公比为
是公比为![]() 等比数列。
等比数列。
![]()
![]()
![]() ……………6分
……………6分
(2)证:![]() ,要证
,要证![]() ,只要证
,只要证![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]() 即
即![]() ………12分
………12分
22.(1)设![]() 则
则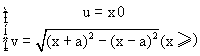
![]() 故所求轨迹
故所求轨迹![]() 的方程为
的方程为![]() ………4分
………4分
(2)由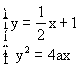 ,得
,得![]() ,
,
由![]() 得
得![]() ……………6分
……………6分
由根与系数关系得![]() ,
,![]()
由![]() 得
得![]()
即![]() (舍去) ………8分
(舍去) ………8分
(3)设上![]() 存在两点
存在两点![]() ,满足:
,满足:![]()
则有![]()
即![]() ……………10分
……………10分
所以![]() 是方程
是方程![]() 的两根,且
的两根,且![]()
![]() ,
,![]() 所以
所以![]()
![]() 解得, ……………12分
解得, ……………12分
![]()
所以,当时![]() ,存在满面足条件的两点;当
,存在满面足条件的两点;当![]()
![]() 时,不存在满足条件的两点。
……………14分
时,不存在满足条件的两点。
……………14分