2005学年
余姚中学 高三年级第三次质量检测数学(文科)试题答题纸
第一学期
命题:赵红庆
一、选择题(每小题5分,共50分)
1. 函数![]() 的最大值是 ( )
的最大值是 ( )
A.![]() B.
B.![]() C.0
C.0![]() D.
D.![]() 2
2
2.函数![]() 的单调递减区间是 ( )
的单调递减区间是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知椭圆![]() 上的一点P到左焦点的距离是
上的一点P到左焦点的距离是![]() ,那么点P到椭圆的右准线的距离是( )
,那么点P到椭圆的右准线的距离是( )
A.2 B.6
C.7 D.![]()
4.在钝角△ABC中,已知AB=![]() ,AC=1,∠B=30°,则△ABC的面积等于 ( )
,AC=1,∠B=30°,则△ABC的面积等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知数列![]() 满足
满足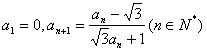 ,则
,则![]() = ( )
= ( )
A.0 B.![]() C.
C.![]() D.
D.![]()
6.从原点向圆 x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为 ( )
A.π B.2π C.4π D.6π
7.与直线![]() 的方向向量共线的一个单位向量是
( )
的方向向量共线的一个单位向量是
( )
A.(3,4)
B.(4,-3) C.![]() D.
D.![]()
8.如图,用4种不同的颜色涂入图中的矩形A、B、C、D中,要求相邻的矩形涂色不同,则不同涂法有( )
| |||||||
C.24种 D.12种
9.点p到点![]() ,
,![]() 及到直线
及到直线![]() 的距离都相等,如果这样的点恰好只有一个,那么a的值是( )
的距离都相等,如果这样的点恰好只有一个,那么a的值是( )
A. B. C. 或 D.- 或
10.设 P(x,y)是曲线 ![]() 上的点,F1(-4,0),F2(4,0),则( )
上的点,F1(-4,0),F2(4,0),则( )
A.|F1P︳+ ︱F2P︳<10 B.|F1P|+|F2P|>10
C.|F1P︳+|F2P︳≤10 D.|F1P|+|F2P|≥10
二.填空题(每小题4分,共16分)
11.设实数x, y满足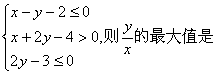 .
.
12.若函数![]() 是奇函数,则a=
是奇函数,则a=
13.在![]() )
)![]() 的展开式中,x3的系数是_________。
的展开式中,x3的系数是_________。
14.已知函数f(x)=2![]()
![]() ,则使得数列
,则使得数列![]() 成等差数列的非零常数p与q所满足的关系式为
.
成等差数列的非零常数p与q所满足的关系式为
.
三、解答题(每小题14分,共84分)
15.设函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)求证:对任意![]() 都有
都有![]() ;
;
(2)若![]() 求
求![]() 的值.
的值.
16.(本小题满分12分)
已知数列![]() 为等差数列,且
为等差数列,且![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)证明![]()
17.解不等式![]()
![]()
18.已知向量![]() ,动点
,动点![]() 到定直线
到定直线![]() 的距离等于
的距离等于![]() ,并且满足
,并且满足![]() ,其中
,其中![]() 是坐标原点,
是坐标原点,![]() 是参数,求动点
是参数,求动点![]() 的轨迹方程,并判断曲线的类型。
的轨迹方程,并判断曲线的类型。
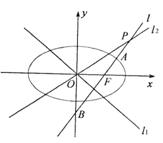
19.已知椭圆C的方程为 ![]() ,双曲线
,双曲线![]() 的两条渐近线为l1,l2 ,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B.(如图)
的两条渐近线为l1,l2 ,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B.(如图)
(1)当l1与l2夹角为![]() ,双曲线的焦距为4时,求椭圆C的方程.
,双曲线的焦距为4时,求椭圆C的方程.
![]() (2)当
时λ的最大值.
(2)当
时λ的最大值.
20。对于![]() 函数,若存在
函数,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点,已知函数
的不动点,已知函数![]() 。
。
(1)
当![]() 时,求函数
时,求函数![]() 的不动点;
的不动点;
(2)
若对任意实数![]() ,函数
,函数![]() 恒有两个相异的不动点,求
恒有两个相异的不动点,求![]() 的取值范围;
的取值范围;
(3)
在(2)的条件下,若![]() 图象上
图象上![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且
的不动点,且![]() 两点关于直线
两点关于直线![]() 对称,求
对称,求![]() 的最小值。
的最小值。
2005学年
余姚中学 高三年级第三次质量检测数学(文科)试题答题纸
第一学期
一.选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二.填空题:本大题共4小题,每小题4分,共16分。将正确答案填在题中横线上.
11. 13。
13. 14。
三.解答题:本大题共6小题,满分84分,每题14分。
15.
16.
17.
18.
19.

20.