![]() 苏州市二区高三调研测试数学试题
苏州市二区高三调研测试数学试题
一、选择题(本大题共12小题,每小题5分,共60分。每小题给出的四个选相中只有一个项是符合题目要求的)
1、![]() 的值是
( )
的值是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2、已知集合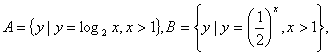 ,则
,则![]() 等于 ( )
等于 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3、函数![]() 的图像经过点
的图像经过点![]() ,则的反函数的图象必过点
( )
,则的反函数的图象必过点
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4、![]() 是两个不重合的平面,在下列条件中,可判定平面
是两个不重合的平面,在下列条件中,可判定平面![]() 与
与![]() 平行的是
( )
平行的是
( )
(A)m,n是![]() 内的两条直线,且
内的两条直线,且![]()
(B)![]() 都垂直于平面
都垂直于平面![]()
(C)![]() 内不共线三点到
内不共线三点到![]() 的距离相等
的距离相等
(D)m,n是两条异面直线,![]()
5、已知数列![]() 的前
的前![]() 项和
项和![]() ( )
( )
(A)一定是等差数列 (B)一定是等比数列
(C)或者是等差数列、或者是等比数列 (D)等差、等比数列都不是
6、给出下列命题:(1)设![]() 是平面内两个已知的向量
是平面内两个已知的向量![]() ,则对于平面内任意的两个向量,都存在唯一的实数
,则对于平面内任意的两个向量,都存在唯一的实数![]() ,使
,使![]() 成立;(2)若定义域为R的函数
成立;(2)若定义域为R的函数![]() 恒满足
恒满足![]() ,则
,则![]() 或为奇函数,或为偶函数。判断下列说法正确的是
( )
或为奇函数,或为偶函数。判断下列说法正确的是
( )
(A)(1)、(2)均为假命题
(B)(1)、(2)均为真命题
(C)(1)为真命题,(2)均为假命题
(D)(1)为假命题,(2)均为真命题
7、若O为坐标原点,抛物线![]() 与过其焦点的直线交于A、B两点,则
与过其焦点的直线交于A、B两点,则![]() 等于(
)
等于(
)
(A)![]() (B)
(B)![]() (C)3
(D)4
(C)3
(D)4
8、在5张卡片上分别写着数字1、2、3、4、5,然后把它们混合,再任意排成一行,则得到的书能被5或2整除的概率是 ( )
(A)0.8 (B)0.6 (C)0.4 (D)0.2
9、已知![]() ,则a的值等于
( )
,则a的值等于
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10、设n为满足![]() 的最大自然数,则n等于 ( )
的最大自然数,则n等于 ( )
(A)4 (B)5 (C)6 (D)7
11、椭圆的一个焦点是(2,1),相应的准线方程是![]() ,椭圆的短轴长为
,椭圆的短轴长为![]() ,则椭圆的另外一个焦点为
( )
,则椭圆的另外一个焦点为
( )
(A)(6,5) (B)![]() (C)
(C)![]() (D)
(D)![]()
12、设函数![]() ,若对任意
,若对任意![]() 都有
都有![]() 成立,则
成立,则![]() 的最小值
( )
的最小值
( )
(A)4
(B)2
(C)1
(D)![]()
二、填空题(本大题共4小题,每小题4分,共16分。把答案填在中的横线上)
13、平面内满足不等式组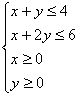 的所有的点中,使目标函数
的所有的点中,使目标函数![]() 取得最大值的点的坐标是
取得最大值的点的坐标是
14、棱长分别为3、4、5的长方体内接于球O,则球的表面积为
15、过点M(1,2)的直线![]() 将园
将园![]() 分成两段弧,其中劣弧最短时,
分成两段弧,其中劣弧最短时,![]() 的方程为
的方程为
16、函数![]() 的图象如图所示,其定义域为
的图象如图所示,其定义域为![]() ,那么不等式
,那么不等式![]() 的解集为
的解集为
三、解答题(本大题共6小题,共74分。解答应写出文字说明,证明过程和演算步骤)
17(本题满分12分)
甲、乙两颗卫星同时监测台风,在同一时段内,甲、乙预报台风准确的概率分别为0.8、0.75,在同一时段内。求:
(1)甲、乙同时预报台风的概率;
(2)至少有一颗卫星预报台风的准确的概率;
(3)若甲独立预报4次,恰有3次预报准确的概率。
20、(本题满分20分)
多面体ABCDE中,![]()
![]()
![]() F为CE的中点。
F为CE的中点。
(1)
求证:![]() ;
;
(2) 求多面体ABCDEF的体积
(3) 求平面BCE与平面ACD所成的角。
21、(本题满分12分)
已知![]() 在上有
在上有![]() 定义,
定义,![]() 且满足
且满足![]() 有
有![]()
(1)
对数列![]() ,求证:数列
,求证:数列![]() 成等比数列
成等比数列
(2)
求证:![]()
22、(本题满分12分,附加题满份4分)
已知曲线C:![]() 及直线
及直线![]() ,曲线
,曲线![]() 关于直线
关于直线![]() 对称。
对称。
(1)
当k=1时,求曲线![]() 的方程
的方程
(2)
k为何值时。曲线C上存在不同两点P、Q关于直线![]() 对称
对称
(3) (本小题为附加题,如果解答正确,加4分,但全卷总分不超过150分)
求证:不论实数k为何值,![]() 恒有公共点
恒有公共点
高三数学参考答案
一、选择题
1、 B;2、A;3、C;4、D5、C;6、A;7、B;8、B;9、C;10、D;11、A;12、B
二、13、(4,0);14、![]() ;15、
;15、![]() ;16、
;16、![]() ;
;
二、解:
17、解、记“甲预报台风准确”为事件A,“乙预报台风的准确”为事件B
![]()
答:甲、乙同时预报台风准确的概率为0.6
![]()
答:至少有一颗卫星预报台风准确的概率为0.95
![]()
答:若甲独立预报4次,恰有3次预报准确的概率为0.4096
18、(1)![]()
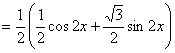
![]()
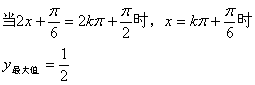
(2)![]() 纵坐标不变,横坐标变为原来的
纵坐标不变,横坐标变为原来的![]() ,得
,得![]()
将![]() 的图象向左平移个单位,得到
的图象向左平移个单位,得到![]()
将![]() 的图象横坐标不变,纵坐标变为原来的
的图象横坐标不变,纵坐标变为原来的![]()
19、证明:(1)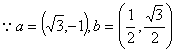
![]()
(2)解:由题意得
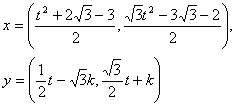
又![]() ,故
,故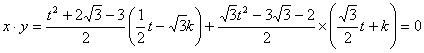
整理得![]()
(3)解:由(2)知: ![]()
![]()
令![]() 故当
故当![]() 时,
时,![]() 是减函数
是减函数
20、(1)证明:取CD的中点G,连接GF、AG
![]() F为CD的中点,
F为CD的中点,
![]() ,即GF=1
,即GF=1
又AB![]() 平面ACD,DE
平面ACD,DE![]() 平面ACE
平面ACE
![]() AB//DE
AB//DE
又AB=1,![]() ,
,
![]()
![]()
![]()
![]()
(2)解:连接BD,则![]()
![]()
(3)解:延长DA、EB交于点P,连接PC,则PC为所求二面角的棱。
![]()
又F为CE的中点,![]()
![]()
![]()
而在Rt![]()
21、(1)证明: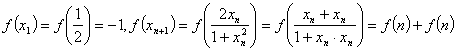
![]() ,既
,既![]() 是以-1为首项,2为公比的等差数列
是以-1为首项,2为公比的等差数列
(2)证明:又(1)知![]()
![]()
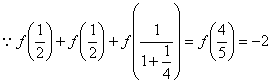
又![]()
![]()
![]()
22、(1)解:设曲线![]() 上任意一点(x、y)关于对称点
上任意一点(x、y)关于对称点![]()
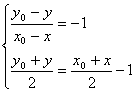 解得
解得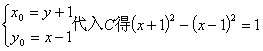
![]()
(2)解:由已知条件设PQ所在的直线方程为:![]()
则有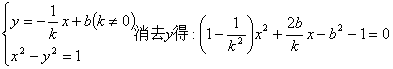
![]() ---------(*)
---------(*)
设PQ中点为M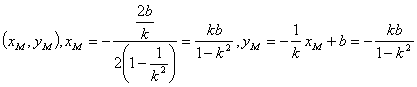
代入![]() 方程得
方程得![]()
即 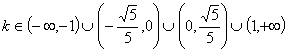
(3)证明:①若C与![]() 有公共点P,则C与
有公共点P,则C与![]() 有公共点且在
有公共点且在 ![]() 上
上
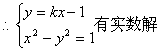
![]()
![]()
![]()
![]()
![]()
②![]()
由②知此时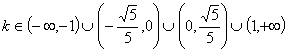
综合①,②,无论k为何值![]()