代数综合练习（二）
2002.4班级：________；姓名：________；成绩：_________
一．选择题：（每小题4分，共4×10=40分）将正确答案填入下表中
▲
1．已知α∈(0,π)且
，则cos2α等于
（A）
（B）
（C）
（D）以上答案都不对
2．先将函数
的周期扩大到原来的3倍，再将其图象向右平移
个单位，则所得函数的解析式是
（A）
（B）
（C）
（D）
3．下列三个命题：①存在实数α,使sinαcosα=1;②存在实数α，使
;
③若cosαcosβ=1，则sin(α+β)=0,其中正确命题是
（A）①和②（B）②和③（C）仅有②（D）仅有③
4．若
，则
，
，1+ctgα的大小关系是
（A）
（B）
（C）
（D）
5．在△ABC中，已知
，则△ABC一定是
（A）等腰三角形（B）直角三角形（C）等腰或直角三角形（D）等腰直角三角形
6．（理）下列各式中正确的是
（A）
（B）
（C）
（D）
（文）下列不等式中正确的是
（A）
（B）
（C）
（D）
7．复数
等于
（A）i（B）-1（C）1（D）0
8．如果复数z=3+ai满足z-2<2,那么实数a的取值范围是
（A）
（B）（-2,2）（C）
（D）（-1,1）
9．设z是虚数，下列命题中不正确的是
（A）若argz=θ则
（B）
，那么z一定是纯虚数
（C）若z=1则
一定是实数
（D）满足z+1-i-z-5-i=6的z在复平面中对应的点集是一条直线
10．在复平面上
，
分别对应复数
，
，向绕点逆时针旋转90°角到向量
的位置，则点
对应复数
（A）
（B）
（C）
（D）
二．填空题：（每小题4分，共4×5=20分）
11．（理）若
，则x的值是_________
（文）若
，则x的取值集合是_____________
12．cos20°+cos100°-cos40°的值是________________
13．复数
的模是____________
14．已知
，
，
为平面上的三个点，又知是线段的中点，且
，
，则
15．△ABC的内角满足sinA+cosA>0,tgA-sinA<0,则角A的取值范围是_______
三．解答题：（每题10分，共40分）
16．求
的值。
17．把曲线
向右平移a(a>0)个单位，得到曲线G，曲线G与曲线C关于直线
对称。（1）求a的最小值；（2）证明当
时，过C上任意两点的直线的斜率恒大于零。
18．已知两个复数集合
，
，且M∩N≠φ，求实数λ的取值范围。
19．已知
，且
为一实数。
（1）求复数w；（2）若z为复数，z=1，求z-w的最大值、最小值。
参考答案
一．1 A 2 C 3 D 4 B 5 C 6 B 7 D 8 C 9 D 10 C
二．11．
12．0
13．625
14．
15．
三．16．
=-4cos36°sin18°
=-1
17．解：
∴
（1）∵曲线C与曲线G关于直线对称
∴对G上的任意点（x,y）点
在曲线C上
∴
∴
∴
∴
，
又a>0∴
(2)对任意
∵
∴
,
∴
,
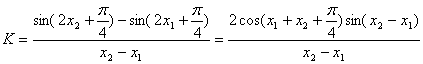
∴k>0
18．解：∵M∩N≠φ∴存在λ∈M且λ∈N
∴
∴
∴
∵
∴
∴
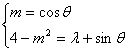
19．解：（1）∵
∴
∴
∵
设
∴
∴
∴
∴
(2)∵
w=-1+I ξ-w表示是(-1,1)到圆
是点的距离
∴
