辽宁省实验中学2002届第四次模拟考试
数学试题
参考公式：
三角函数的积化和差公式
正棱台、圆台的侧面积公式
其中
、c分别表示上、下底面周长，l表示斜高或母线长
台体的体积公式
其中
、S分别表示上、下底面积，h表示高
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
（1）函数
的最小正周期是
（A）
（B）π
（C）2π （D）4π
（2）若a<b<0，则下列结论中正确的是
（A）不等
都不成立
（B）不等式
都不成立
（C）不等式
都不成立
（D）不等式
都不成立
（3）空间四边形ABCD中，AB=CD，E、F分别是AD、BC的中点，下列四个结论中正确的是（ ）
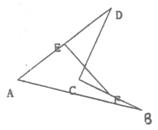
（A）∠AEF=∠BFE （B）AD⊥BC
（C）AB⊥CD （D）EF与AB和CD成角相等
（4）将离心率为
的椭圆
绕其左焦点按顺时针方向旋转，所得新椭圆的一条准线方程是
，则新椭圆的另一条准线的方程是
（A）
（B）
（C）
（D）
（5）将函数
的图象沿x轴
（A）向右平移一个单位 （B）向左平移一个单位
（C）向上平移一个单位 （D）向下平移一个单位
所得图象与函数
的图象关于y轴对称
（6）已知复数2-i的辐角主值是θ，则
的辐角主值是
（A）
（B）
（C）
（D）
（7）（理）使
成立的x的取值范围是
（A）
（B）
（C）
（D）
（文）满足
且
的角x的取值范围是
（A）
（B）
（C）
（D）
（8）在
的展开式中x的系数是
（A）160 （B）240
（C）360 （D）800
（9）某商店卖A、B两件价格不同的商品，由于商品A连续两次提价20%，同时商品B连续两次降价20%，结果都以每件23.04元售出，若商店同时售出这两种商品各一件，则与价格不升不降的情况比较，商店盈利情况是
（A）多赚5.92元 （B）少赚5.92元
（C）多赚28.92元 （D）盈利相同
（10）直角梯形的一个内角为45°，下底长为上底长的
，这个梯形绕下底所在的直线旋转一周所成的旋转体的全面积为
，则旋转体的体积为
（A）
（B）
（C）
（D）
（11）
表示一个公比
的等比数列的前n项和，记
，那么集合M的子集个数是
（A）2个 （B）4个
（C）7个 （D）8个
（12）设二次函数
满足
，且其图象开口向上，若
（其中
），则p、q、r的大小关系是
（A）p>q>r （B）q>p>r
（C）q>r≥p （D）q>p≥r
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
（13）已知函数
在
上是减函数，则实数a的取值范围是_________________。
（14）某同学从6门课中选学2门，其中有两门课上课时间有冲突，另外有两门课不允许同时选学，则可选学的方法总数有___________种。
（15）方程
的两个解的和是_________________。
（16）设
，M是双曲线
上位于第一象限的点，给出3个命题：①
；②以线段
为直径的圆与圆
相切；③存在常数b，使M到直线
的距离等于
；
其中正确命题的序号是____________。
三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
（17）（本小题满分12分）
在△ABC中，三内角A、B、C满足
，若
，且三边满足
。
求三边a、b、c的长度。
（18）（本小题满分12分）
已知
，且
是一个递增的等差数列
的前三项。
求数列的通项公式及
的值。
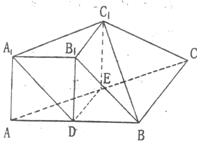
（19）（本小题满分12分）
在三棱台
中，已知
面ABC，
，且
和底面ABC成的角是45°，
面
。
（Ⅰ）求证：BC⊥面
；
（Ⅱ）求异面直线
与
所成角的正切值；
（Ⅲ）求多面体
的体积。
（20）（本小题满分12分）
某电脑公司准备将100台同类型的电脑租给某大学的学生。根据市场调查，如果每台电脑每月租金不高于100元，可全部租出；如果每台电脑每月租金高出100元，那么每提高10元将有5台电脑闲置。为了提高公司的经济效益，该公司需要拟定一个最佳月租价格，这个价格必须满足：
①为了便于核算，月租价定为10元的整数倍；
②由于公司的开支（如员工工资，水电费等）每月需要6250元，电脑出租收入必须高于支出，而且高出得越多越好。
（Ⅰ）把该公司的每月净收入y（即收入减支出）表示为每台电脑月租金x元的函数，并求出其定义域；
（Ⅱ）求每台电脑的月租金x为多少时，公司的净收入y最大，并求出最大值。
（21）（本小题满分13分）
已知函数
为奇函数。
（Ⅰ）求f（x）的解析式；
（Ⅱ）解关于x的不等式
，其中
。
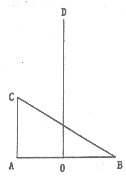
（22）（本小题满分13分）
如图，在△ABC中，
于O点，OA=OB，DO=2，曲线E经过C，动点P在E上运动，且保持PA+PB的值不变。
（Ⅰ）建立适当的坐标系，求曲线E的方程；
（Ⅱ）过点D的直线l与曲线E相交于不同的两点M、N，且M在D，N之间，设
，求λ的取值范围。
辽宁省实验中学2002届第四次模拟考试数学试题
参考答案
一、BBDCB CDBBB BD
二、（13）-8<a≤-6
（14）13
（15）-99
（16）①②③
三、（17）解：由已知得
由△ABC中 
得
……2分
有
得
……4分
则有
得cos（B+C）=0
故
得
……7分
由题意得
……9分
解得a=5，b=4，c=3。 ……12分
(18)解：由已知得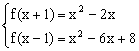
……2分
由
……4分
则有
……6分
……8分
……12分
（19）（1）证明：∵
⊥底面ABC，BC
底面ABC，
∴
……2分
又∵
⊥BC，与共面必相交，
∴BC⊥平面
……4分
（2）∵//平面
，
∴
，
∵
，
∴四边形
是正方形，
∵和底面ABC成角为45°，即
，
∴
∴
即为与所成的角
……6分
∴
……8分
（3）
……12分
（20）解：（1）设每台电脑月租金为x（元），
当x≤100时，有y = 100x - 6250，可得
。
这时
……3分
当x>100时，闲置电脑
（台）
每月收入为
则有
由y>0，x>100，解得100<x<250， ……6分
综上所求函数为：
……8分
（2）若x≤100，y ={100x - 6250增函数，
故x=100时，
，
若x>100时，当x=150时，
，
……10分
故每台电脑月租金为150元，收入最大为5000元 ……12分
（21）解：（1）由
得f(x)定义域： （-1，1） ……2分
∵f(x)是奇函数，
∴f(-x)= - f(x)
即
得
∵
∴1 + a = 0，即a = -1 ……4分
∴
……6分
（2）由
得
……8分
由，得
……①
当
时，由①得
……10分
∴当时，不等式的解为
。
当
时，不等式无解，
当m>1时，不等式的解为R，
当
时，①恒成立
……12分
综上所述：
当时，不等式无解，
当时，不等式的解为
当
时，不等式的解为R，
……13分
（22）解：（1）以AB、OD所在的直线分别x轴、y轴，O为原点建立坐标系。
∵
，
……4分
∴动点的轨迹是椭圆，
设其长、短半轴为a、b，半焦距c，
则
，c=1，b=1
∴曲线E的方程为
。
……6分
（2）设L：y = kx + 2代入椭圆方程
得
，
整理得
设
，
则
，
即
……8分
①当L与y轴重合时，
……9分
②当L与y轴不重合时，由，
∵
，
或
∴0<λ<1，
∴
。
∵
，
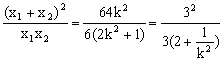得
得
……12分
综合①、②得λ取值为
……13分