宜州市高中高三月考数学试卷
（120分钟 150分）
参考公式：
三角函数的和差化积公式
，
，
，
，
正棱台、圆台的侧面积公式
其中c′、c分别表示上、下底面周长，l表示斜高或母线长
台体的体积公式
其中S′、S分别表示上、下底面积，h表示高
第I卷 （选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．设全集I=R，A={-1}，
，则以下
的是（ ）
A．
B．
C．A∪B=φ D．
2．设等比数列
的前n项和为
，若
，则此数列的公比q为（ ）
A．2 B．4 C．3 D．5
3．正方体
中，E为
的中点，过点E作一条直线与
和AB都相交，这样的直线（ ）
A．不存在 B．仅有一条 C．有两条 D．有三条
4．已知
，则它们的图象经过平移，可使（ ）
A．
重合
B．
重合，但不能与
重合
C．
重合，但不能与
重合
D．
重合，但不能与
重合
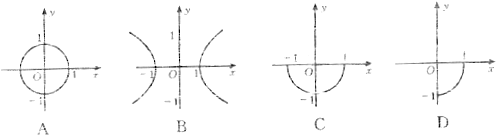
5．方程
所对应的曲线图形是（ ）
6．设A、B两点的坐标分别为（-1，0），（1，0）。条件甲：A、B、C三点构成以∠C为钝角的三角形；条件乙：点C的坐标是方程
（y≠0）的解，则甲是乙的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分又不必要条件
7．高三年级的三个班去甲、乙、丙、丁四个工厂进行社会实践，其中工厂甲必须有班级去，每班去何工厂可自由选择，则不同的分配方案是（ ）
A．16种 B．18种 C．37种 D．48种
8．若函数y=f(x)存在反函数，则方程
的解的个数是（ ）
A．0或2 B．0或1或2 C．1或2 D．2
9．圆A：
，点B（c，0），其中c>a>0，M是圆A上的动点，MB的中垂线交MA所在的直线于P，则点P的轨迹（ ）
A．椭圆 B．双曲线 C．抛物线 D．直线
10．若
，sinθ=a（
），则
等于（ ）
A．
B．
C．
D．
11．如图，一个无盖的长方体容器，AB=2，BC=3，现将容器盛满水，然后固定
，将容器倾斜，让水流出，当容器中的水是原来的时，平面
与水平面所成的角为
，同样可固定
，也将容器倾斜，让水流出，当容器中的水是原来的时，平面
与水平面所成的角为
，则（ ）
A．
B．
C．
D． 不能确定
12．抛物线
的顶点在椭圆
上，这样的抛物线有且只有二条，则m的取值范围是（ ）
A．（0，1） B．（-∞，1） C．（1，+∞） D．（-∞，+∞）
第II卷 （非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
13．若a>b>0，且
，则m的取值范围是____________。
14．把直线
绕点（1，1）顺时针旋转，使它与圆
相切，则直线转动的最小正角是____________。
15．某企业去年销售收入1000万元，年成本分为年生产成本500万元与年广告费成本200万元两部分。若利润的p%为国税，且年广告费超出年销售收入2%的部分也必须按p%征国税，其他不纳税，已知该企业去年共纳税120万元，则税率p%为____________。
16．如果一个四面体的三个面是直角三角形，下列三角形：①直角三角形；②锐角三角形；③钝角三角形；④等腰三角形；⑤等腰直角三角形。那么可能成为这个四面体的第四个面的是____________（填上你认为的序号）。
三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
17．（本小题满分12分）
已知复数
。
（1）求
的辐角主值；
（2）若△ABC的三内角A、B、C均不大于
，且
，
，试判断三角形ABC的形状。
18．（本小题满分12分）
如图，斜三棱柱
，已知侧面与底面ABC垂直且∠BCA=90°，
，
，若二面角
为30°。
（1）证明
；
（2）求
与平面所成角的正切值；
（3）在平面
内找一点P，使三棱锥
为正三棱锥，并求P到平面
的距离。
19．（本小题满分12分）
已知函数
定义在区间[0，1]上，
且
，f(0)=f(1)。
（1）求a的值；
（2）证明：
。
20．（本小题满分12分）
水土流失是我国西部大开发中最突出的生态问题，全国9100万亩的25度以上的坡耕地需要退耕还林，其中西部地区占70%，2000年国家确定在西部地区退耕土地面积为515万亩，以后每年退耕土地面积递增12%。
（1）试问从2000年起，到哪一年西部地区基本解决退耕还林问题？
（2）为支持退耕还林工程，国家财政补助农民每亩300斤粮食，每斤粮食按0.7元折算，并且每亩退耕地每年补助20元，试问：到西部地区基本解决退耕还林问题时，国家财政共需支付约多少亿元？
（精确到亿元，参考数据：
，
，
）
21．（本小题满分12分）
已知双曲线S的两条渐近线过坐标原点，且与以点A（
，0）为圆心，1为半径的圆相切，双曲线S的一个顶点A′与点A关于直线y=x对称，设直线l过点A，斜率为k。
（1）求双曲线S的方程；
（2）当0≤k<1时，若双曲线S的上支上有且只有一个点B到直线l的距离为，求斜率k的值及相应的点B坐标。
22．（本小题满分14分）
已知函数f(x)满足f(a+b)=f(a)·f(b)且
。
（1）当n∈N时，求f(n)的表达式；
（2）设
，n∈N，求证：
；
（3）设
，n∈N，
，求
。
参考答案：
1．D 2．C 3．B 4．A 5．D 6．B 7．C 8．B 9．B 10．B 11．A 12．A
提示：
3．由E与所确定的平面与由E与AB所确定的平面有且只有一条过E的公共直线，该线与AB和都相交。
5．可用排除法：当x=0时，y=-1，排除A，B；当y=0时，x=1，排除C。
6．数形结合：（-1，0），（1，0）是椭圆两端点，以AB为直径作圆，由图可知∠AC′B=90°，而∠ACB>90°，故选B。
9．PM=PD而PA=PM+AM或PA=PM-AM，得PA-PM-AM，∴PA-PB=2a，∴P点的轨迹是双曲线。
10．
，
11．固定时，倒出水的体积
，固定时，倒出水的体积
，
，
，得
。
12．
。故抛物线的顶点坐标为（sinα，
）代入椭圆方程得
，即
，所以
，因为这样的抛物线仅有两条，
必须无解，得m<1，又m>0，∴0<m<1。
13．（-b，0）
14．60°
15．25%
16．①②④⑤
17．（1）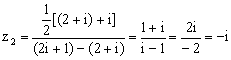
。
的辐角主值为
。…………（4分）
（2）
。
………………………………（8分）
法1：
得A+C=或
故△ABC为直角三角形。 （12分）
法2：
∴A+C=或
，舍去
∴ABC为直角三角形。………………………………（12分）
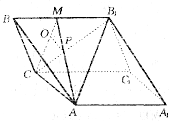
18．（1）证明：∵∠BCA=90°，∴AC⊥BC，又侧面⊥底面ABC，
∴AC⊥平面………………………………（3分）
（2）连结
，则∠A为直线与平面所成的角，过C作CM⊥
于M，连结AM，则∠CMA为二面角A--C 的平面角，∠CMA=30°。经计算，可得-2，CM=
。AC=1，在Rt△A
中，tg∠A=…………（7分）
（3）在正三角形
中，在CM上取三分点O，使CO=2OM，则O为△的中心，过O作AC的平行线OP交AM于P，点P即为所求点，可算得
………（12分）
19．解：（1）f（0）=c，f(1)=1+a+c
∴c=1+a+c，得a=-1。………………………………（4分）
（2）法1：
，而
，
………………………………（8分）
故
………………………………………………（12分）
法2：
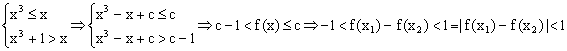……………………………………………………………………（12分）
法3：
………………………………………………（8分）
若
，则
，
另一方面
相加得。……………………………………（12分）
20．氧气瓶中氧气的体积，
≈17（升）………………………………（4分）
设返回水面过程中的每分钟需氧量为Q，则
，
因当速度为1米/分，每分钟需要氧量0.2升，
所以k=0.2，故来回途中需氧量为20×0.2v+20×0.2/v。………………（8分）
在湖底的工作时间为[17-(4v+4/v)]/0.4，
∵[17-(4v+4/v)]/0.4≤22.5
因此，潜水员在湖底最多能工作22.5分。…………………………（12分）
21．解：（1）由条件知A（0，），……………………………………（2分）
设渐近线的方程为y=k′x，
，得k′=±1，
∴双曲线的方程为
。……………………（5分）
（2）设l′为y=kx+m且
，
，
则l′是与l平行且相距为的平行线，取l上方的一条，即
，
这样只需考虑l′与上支有且只有一个交点，
∴y=kx+m代入得
。
由△=0得k=0或
，
当k=0时
得B（0，）。
时，得
……………………………………（12分）
22．解：（1）由已知得
……………（5分）
（2）由（1）知
，设
，
则
所以
，两式相减可得
，
所以T<2，结论成立。……………………………………（10分）
（3）
，所以
，
所以
……………（14分）