2001—2002学年第一学期期末高三数学试题
一、选择题：（本大题共12道小题，每小题5分，共60分）
1．在等差数列
中，
，则
等于
A．3 B．4 C．6 D．12
2．如果
且
，则f(x)可以是
A．sin2x B．cosx C．sinx D．sinx
3．题设：平面α、β、γ直线l、m满足：α⊥γ，γIα=m，γIβ=l，l⊥m，结论：①β⊥γ；②m⊥β；③α⊥β，那么由题设可以推出的正确结论是
A．①和② B．③ C．②和③ D．①和③
4．从1、2、3…，100这100个数中任取两个数相乘，如果乘积是3的倍数，则不同的取法有
A．
B．
C．
D．
5．若复数z满足z+2i+z-2i=4，记z+1+i的最大值和最小值分别为M，m则
等于（ ）
A．2
B．
C．
D．
6．过抛物线
的焦点F做直线与抛物线交于P，Q两点，当此直线绕其焦点F施转时，弦PQ中点的轨迹方程为（ ）
A．
B．
C．
D．
7．设复数
，
，则
等于（ ）
A．
B．
C．
D．
8．将长为2πcm，宽为πcm的长方形纸片围成一个容器（不考虑底面及粘接处），立放于桌面上，下面四个方案中，容积最大的是
A．直三棱柱 B．直四棱柱 C．高为π的圆柱 D．高为2π的圆柱
9．椭圆
的一条准线为x=7，则随圆的离心率等于
A．
B．
C．
D．
10．在正方体
中，EF为异面直线
和AC的公垂线，则直线EF与
的关系是
A．异面 B．平行 C．相交且垂直 D．相交但不垂直
11．（理）在极坐标系中，点
到直线
的距离等于
A．2
B．1 C．
D．
（文）自点（-1，4）作圆
的切线，则切线长为
A．5 B． C． D．3
12．某工厂8年来某种产品总产量c与时间t（年）的函数关系如图，下列四种说法：①前三年中，产量增长的速度越来越慢；②前三年中，产量增长的速度越来越快；③第三年后，这种产品停止生产；④第三年后，年产量保持不变，其中说法正确的是（ ）
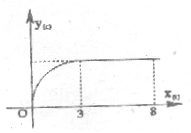
A．②与③ B．②与④ C．①与③ D．①与④
二、填空题：（本大题共四道小题每小题4分共16分）
13．已知曲线C与曲线
关于直线x-y=0对称，则曲线C的焦点坐标为_________。
14．若
展开式中的第5项为常数项，则n=___________。
15．现有三个电阻，串联后的电阻为R，并联后的电阻为r，令
，则t的取值范围是________________。
16．
三、解答题：（本大题共六道小题，17—21小题每题12分，22题14分共74分）
17．已知复数z满足
为纯虚数
（1）求z； （2）若
，求z。
18．某厂生产一种产品，使用的两种原料的价格随月份发生波动，生产每一件产品所需这两种原料的资金
（元），
（元）与月份t的关系式为：
，
，
预计每件产品的其它费用为100元，且保持每件产品的利润总为50元。
（1）求每月产品的出厂单价
与月份t的关系式，并求出的最大最小值。
（2）若产品出厂后一个月才上市出售，且商店利润为10%，求该产品的市场价格
与月份t的关系式。
19．已知数列中，
，
（1）求
的值。
（2）推测数列的通项公式，并用数学归纳法证明所得的结论。
（3）求
20．（文科做①、②，理科做①、②、③）
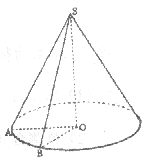
设SA、SB是圆锥SO的两条母线，O是底面的圆心，底面半径为10cm，C是SB上一点。
①求证：AC与平面SOB不垂直；
②若∠AOB=60°，C是SB的中点，AC与底面所成的角为45°，求O到平面SAB的距离；
③在②的条件下，求二面角O—SB—A的大小。
21．已知椭圆
（m>0，n>0）有共同的焦点
，设P为椭圆和双曲线的交点。
①求
的值；
②当b=n时，求证：
。
22．设0<a<1，函数
，设f(x)和g(x)的定义域的公共部分为D，求当
，f(x)在
上的值域是[g(n)，g(m)]时a的取值范围
高三数学参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | B | B | C | A | D | C | A | B | D | C |
二、填空题：
13．
14． 12
15． t≥9
16．
三、解答题：
17．（1）设
解得
，……………………3分
所以
………………………………………6分
（2）设
，则
……………………9分
因为z=4，所以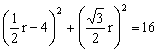
即r=4 所以
…………………………………………………………12分
18．①依题意
当t=11时，有最大值680元，当t=5时，有最小值620元………………6分
②依题意知
………………………………12分
19．
即
即
即
………………………………3分
（2）猜想
………………………………………………5分
证明：①当n=1时，
结论成立
②假设n=k时结论成立，即
则
由
即
，得
说明当n=k+1时结论也成立。
由①②可知，对于一切
都有………………………………10分
（3）
………………………………12分
（20）
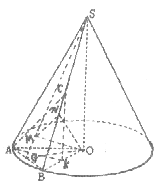
（1）证明：假如AC⊥平面SBO QSO⊥底面AOB，
∴平面SBO⊥底面AOB，交线为BO，
做AD⊥BO于D，则AD⊥平面SBO又AC⊥平面SBO
∴AC∥AD，这与AD∩AC=A矛盾，
因而假使不成立，即AC与平面SBO不垂直………………………………4分
（2）作CK⊥OB于K，连AK、ACQ平面SBO⊥底面AOB
∴CK⊥底面AOB，则∠CAK是AC与底面AOB所成的角∠CAK=45°。又C是SB的中点，CK∥SO
∴
，
在Rt△ACK中
，∴
设G为AB中点，连接OG、SG则AB⊥GO，AB⊥SG，∴AB⊥平面SGO，平面SAB⊥平面SGO，过O作OM⊥SG于M，则OM⊥平面SAB
在Rt△SGO中，点
∴点到平面的距离为
………………………………9分
③过O作ON⊥SB于N，连接MN，
则∠ONM为二面角O-SB-A的平面角，
在Rt△SBO中，
，
在Rt△ONM中，
∴二面角O-SB-A为
………………………………12分
21．解：（1）设点P(x，y)为曲线交点
则
①
②………………………………………………………………3分
得
即
……………………………………………………6分
（2）方法1：由
得：
，…………………………8分
而
…………………………………………………………10分
…………………………………………12分
方法2：用
也可证明；
方法3：在
中，
…………………………………………………………………………………………10分
当n=b时 
即 ………………………………………………………………12分
22．解：可以求得f(x)的定义域为
，g(x)的定义域为
∴D=
…………………………………………3分
又
令
，则t在D上是增函数
∴0<a<1是，f(x)在D上是减函数，g(x)在D上也是减函数。
∴f(x)，g(x) 在[m，n]上都是减函数。
∴3<m<n………………………………………………………………………………4分
且有
∴m，n是方程f(x)=g(x)的两个相异实根……………………………………………………6分
即m、n是方程
的两个大于3的相异实根……………………8分
令
它表示开口向上的抛物线
∴有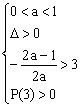
………………………………………………………………10分
即
………………………………………………………………12分
∴
………………………………………………………………14分