数学试题(理科)答案
一、选择题答题卡:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | A | B | A | C | B | D | B | A | D | C |
二、填空题答题卡:
13. ![]() 14. a<c<b
14. a<c<b
15. ![]() 16. 23
16. 23
三、解答题:(共6小题,74分,解答题应写出文字说明,证明过程及演算步骤)
17、
解:(1)设![]()
(2)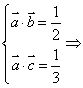
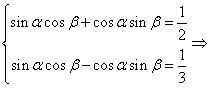
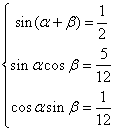
![]() 原式
原式![]()
18、
解:(1)当![]() 时,
时,![]()
当![]() 时,
时,![]()
![]()
![]() 当
当![]() ,
,![]() 即
即![]()
故
(2)![]()

![]()
![]()
![]()
![]()
![]() =
=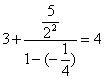
19、
解:(1)![]() (2)原式=
(2)原式=![]()
![]() =
=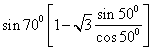
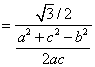 =
=![]()
=![]() =
=![]()
![]() =
=![]()
![]() =
=![]()
![]() 在锐角
在锐角![]() 中
中![]()
20、解:在甲图中:连结OM,设![]()
![]() S矩=
S矩=![]()
![]() 当
当![]() 时
S矩/max=
时
S矩/max=![]()
在乙图中,同理连结MO,设![]() 则由
则由![]() 可知:
可知:
![]()
![]()
![]() =
=![]()
同理![]() 又在
又在![]() 中,CD=
中,CD=![]()
![]()
![]() 矩
矩![]()
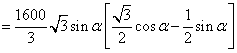
![]()
![]() 当
当![]() 时S’矩/max
时S’矩/max![]()
故乙方案裁法能得到最大面积矩形,最大值为![]()
21、
解:①![]()
![]()
由![]() ,即
,即![]()
但![]() 对
对![]() 不可能恒成立
不可能恒成立
![]() 对
对![]() 不可能恒成立
不可能恒成立
![]() 在
在![]() 不能单调递减,只能单增
不能单调递减,只能单增
又由![]() ,得
,得![]() ,对
,对![]() 恒成立,
恒成立,![]()
![]()
又![]()
![]()
![]()
![]() 在
在![]() 单增 且
单增 且 ![]() 而
而![]()
![]() 当且仅当
当且仅当![]() ,即
,即![]() 时,
时,![]()
证②:设![]() ,则
,则![]()
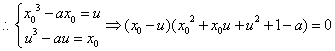
![]() ,且
,且![]()
![]()
![]()
![]() ,即
,即![]() 故
故![]()
注:①可用定义法 ②可用反证法
22、
证(I):![]() 、
、![]() 有
有![]()
![]() 取
取![]() 则
则![]()
![]() 时
时![]()
![]()
又设![]() 则
则![]()
![]()
![]()
而当![]() 时,
时,![]()
![]() 当
当![]() 时
时 ![]()
(II):①![]()
由![]() 得
得![]()
![]()
![]()
可证![]() 是R的递减函数,证明如下:
是R的递减函数,证明如下:
设![]() 、
、![]() 且
且![]() 则
则![]()
![]()
即![]()
![]() 是
是![]()
![]() 即
即![]()
![]()
②设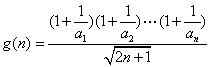 ,得
,得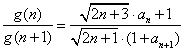
![]()
![]()
![]() 即
即![]()
![]() 对
对![]() 单增
单增
而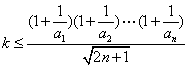 即
即![]() 对
对![]() 恒成立
恒成立
![]() 即
即![]()