高三第二次统考（理）答案
一、CDCCA，CDCAB，DC
二、13 — 
14 
15 
16 
三、解答题部分
17、（1）
+
=
=
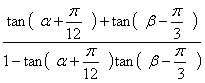
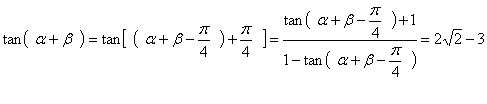
18、解：
在[1、4]上恒成立。
设
即
在[1，2]上恒成立
设
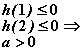
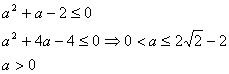
19、（1）证明：任取
，则：
由已知
即
在[-1，1]上为增函数
（2）在[-1，1]上为增函数
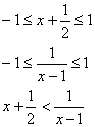解得
20、证明：（1）令
为增函数
又
当
时，
即
(2)不妨设
为增函数，即
令
)
所以
为减函数，即
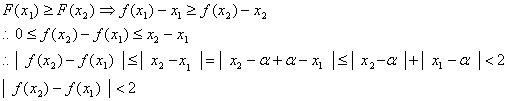
方法2
（1）
点
两点的斜率为
根据导数的几何意义，存在一点
使得
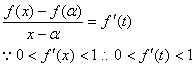
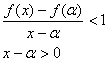
当
不等式显然成立
当
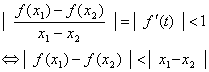
又
综上得
21、（1）设
在
上是增函数
所以
既
成立。
（2）原不等式等价于
令
令
列表如下：
| x | -1 | (-1,0) | 0 | (0,1) | 1 |
|
| 0 | + | 0 | — | 0 |
|
| 极小值 |
| 极大值 | ↘ | 极小值 |
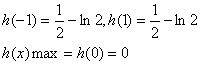
当
时，
令
,则
在[-1，1]为非负正数
得
或
22、解：
令
则
|
|
|
|
| 3 |
|
|
| - | 0 | + | 0 | - |
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
（1）
时， 函数取得极大值
时，
即
时,
即 即
↗
而所求的
的取值范围是
,
（2）由（1）知在
上是增函数。
（3）当
故在[0、3]上为增函数。
故在[0、3]上的值域为
而
在[0、3]上为增函数，所以
的值域为
=
由假设知
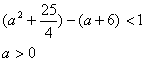
故的取值范围是：（
）