浙江省嘉兴市高三教学测试（一）文科数学试题卷2007年3月
本测试共三大题，有试题卷和答题卷．试题卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷（选择题）采用机读卡答题的考生请将答案涂写在机读卡上，不采用机读卡的考生请将答案填在答题卷上．第Ⅱ卷（非选择题）答案都填写在答题卷上．
第Ⅰ卷
一．选择题（本大题共10小题，每题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1．设
，
，则
（A）
（B）
（C）
（D）
2．计算
（A）
（B）
（C）
（D）
3．某中学有高一学生400人，高二学生300人，高三学生500人，现用分层抽样的方法在这三个年级中抽取120人进行体能测试，则从高三抽取的人数应为
（A）40 （B）48 （C）50 （D）80
4．函数
的图像是
 |
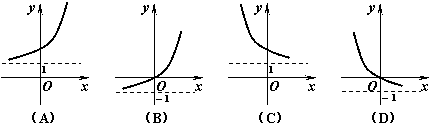5．已知A、B、C三点共线（该直线不过原点O），若
，则
（A）
（B）
（C）
（D）
6．已知直线
，平面
，则使
成立的一个充分条件是
（A）
（B）
（C）
（D）
7．若
展开式的第5项等于
，则x的值是
（A）2 （B）
（C）
（D）
8．有5人排成一排照相，其中甲、乙两人必须相邻且不排在两头，则不同的排法共有
（A） 12种 （B） 18种 （C） 24种 （D） 36种
9．反比例函数
的图象是双曲线，则它的一个焦点坐标是
（A）
（B）
（C）
（D）
10．已知正四面体
，点
为侧面
内的一个动点，且点
与顶点
的距离等于点到底面
的距离，那么动点的轨迹是某曲线的一部分，则该曲线是
（A）圆 （B）椭圆 （C）双曲线 （D）抛物线
第Ⅱ卷
二．填空题（本大题共4小题，每题4分，共16分）
11．已知函数
，若
，则
▲ ．
12. 已知向量
，若
，则k的取值范围是 ▲ ．
13．平行于直线
，且经过点
的直线方程是 ▲ ．
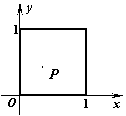14．设A、B是两个平面区域，面积分别为
、
，且
，则区域A内的随机点落在区域B内的概率
．已知
是如图所示正方形内的随机点，那么长度为
、
、1的三条线段能构成钝角三角形的概率是 ▲ ．
三．解答题（本大题共6小题，每题14分，共84分）
15．已知函数
，求
的最小正周期及单调递增区间．
16．某中学排球比赛采用三局二胜制，现有甲、乙两班进行比赛，已知每局比赛中甲班胜乙班的概率是
．
（1）若乙班已经在第一局中获胜，求乙班最终取得胜利的概率；
（2）若胜一局得2分，负一局得
分，求甲班最终得3分的概率．
17．已知函数
．
（1）求证：在定义域R上是增函数；
（2）曲线
的倾斜角最小的切线方程．
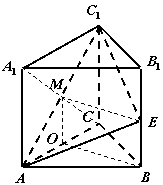
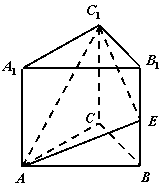18．在正三棱柱
中，
，E是棱
的中点．
（1）求证平面
平面
；
（2）求AE与平面所成角的大小；
19．数列
中，
，
，且
．设数列前
项的和为
，
．
（1）求
的值；
（2）求证
．
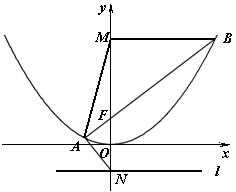
20．已知抛物线
，过焦点F的直线与此抛物线交于
、
两点，设M是点B在y轴上的射影，准线l与y轴交于点N．
（1）求证：
；
（2）若AB⊥AN，
①求证：
；
②求证：∠MAB＝∠MBA．
嘉兴市高三教学测试（一）文科数学参考答案2007年3月
一．选择题（本大题共10小题，每题5分，共50分）
1．D ； 2．C； 3．C； 4．B； 5．A；
6．C； 7．A； 8．C； 9．D； 10．B.
二．填空题（本大题共4小题，每题4分，共16分）
11．
； 12.
； 13．
； 14．
.
三．解答题（本大题共6小题，每题14分，共84分）
15．
，（…6分）
最小正周期
，（…4分）
单调递增区间为
（
）．（…4分）
16．（1）
；（…6分）
（2）甲班最终得3分的胜负情况是：“胜负胜”或“负胜胜”，
∴
．（…8分）
17．（1）
．（…4分）
∵
，∴在定义域R上是增函数；（…3分）
（2）∵
，（…3分）
而
，曲线在
的切线倾斜角最小．
方程为
，即
．（…4分）
18．方法一：
（1）连
交
于M，则M是的中点，取AC中点O，连OM、OB、EM，则OBEM为矩形，∴
．（…2分）
∵
，平面
平面，
∴
平面．（…2分）
∴
平面，从而平面平面．（…2分）
（2）∵平面，（…2分）
∴
就是AE与平面所成的角．（…2分）
在Rt△EAM中，
，
，∴
．
∴AE与平面所成的角为
．（…4分）
18．方法二：
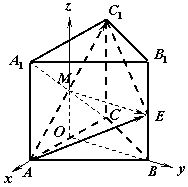（1）连交于M，则M是的中点，取AC中点O，连OM、OB，则OA、OB、OM两两互相垂直，建立空间直角坐标系
．（…2分）
∵
，
，∴
．（…2分）
∴
平面
．
而
平面
，∴平面平面．
（…2分）
（2）∵
，（…2分）
．（…2分）
∵
．
∴AE与平面所成的角为．（…4分）
19．（1）∵，，，
∴的奇数项构成等差数列，首项为0、公差为2，（…2分）
的偶数项构成等差数列，首项为3、公差为2．（…2分）
∴
．（…4分）
（2）∵
，（…2分）
∴
．（…2分）
∴
．（…2分）
20．（1）
，设AB：
（显然直线AB斜率存在）．（…2分）
由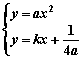
．∴
，
．
∴
．（…4分）
（2）①
，∵AB⊥AN，∴
．（…2分）
又
，
，∴
．（…2分）
（2）①另解：易证△ANF∽△MBF，
MF=
，AF=
，BF=
，FN=
，即
，
由等比定理得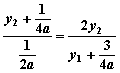
，化简整理得
（2）②
，设AB中点为
，则
，
．
∴
，∴
．
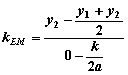
∴△MAB是等腰三角形，
，故∠MAB＝∠MBA．（…4分）
（2）②另解：，EM=x2,EA=
,
由（2）①得
，∴
，EA=
，
又由（1）得，∴
，即
，
∴EM=EA，∴△MAB是等腰三角形，即∠MAB＝∠MBA．
命题人：屠新跃、钱卫红、吴明华