数学理科 模拟试卷六
一、选择题
1. 已知:I为全集,集合PI,SI,则下列集合中,与![]() ∪
∪![]() 相同的集合是( )
相同的集合是( )
(A) ![]() (B)
(B)
![]()
(C) ![]() ∩
∩![]() (D) 空集
(D) 空集
2. 若复数1+i,-2+i,3-2i分别对应复平面上的点A、B、C,线段BC的中点为D,
则向量![]() 对应的复数是:( )
对应的复数是:( )
(A)-![]() -
-![]() (B)
(B) ![]()
(C) ![]() (D)
(D)
![]()
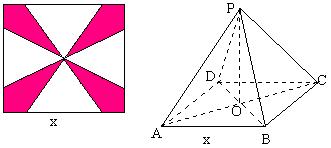
3. 已知函数![]() (x≠-a) 的图象关于直线y=x对称,则必有:( )
(x≠-a) 的图象关于直线y=x对称,则必有:( )
(A) a可为任意实数 (B) a=0
(C) a=1 (D) a=0.1
4. 下列命题中,正确的是:( )
(A) 一条直线垂直于一条斜线在平面内的射影,则此直线垂直于该斜线
(B) 两条直线在同一个平面内的射影平行,则这两条直线平行或垂直
(C) 与两条异面直线都平行的平面有且仅有一个
(D) 如果一个平面垂直于另一个平面内的一条直线,那么这两个平面垂直
5. 圆 x![]() +y
+y![]() -4x+2y+c=0 与y轴交于A、B两点,设这个已知圆的圆心为P,
-4x+2y+c=0 与y轴交于A、B两点,设这个已知圆的圆心为P,
且∠APB=90°,则C的值等于( )
(A) -3 (B) 8
(C) 3
(D) ![]()
6. ![]() 的值等于( )
的值等于( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
7. 若 ![]() (n∈N) 展开式中含有常数项,则n的最小值是( )
(n∈N) 展开式中含有常数项,则n的最小值是( )
(A) 4 (B) 5
(C) 6 (D) 8
8. m个男同学,n个女同学排成一行,左边第一个必须排男同学,右边第一个必须排女同
学的不同排法种数是:( )
(A) ![]() (B)
(B)
![]() ·
·![]()
(C) mn(m+n-2)
(D) ![]()
9. 命题“棱柱的侧面是全等的矩形”是命题“棱柱是正棱柱”的( )
(A) 充分但不必要条件
(B) 必要但不充分条件
(C) 充要条件
(D) 既不充分也不必要条件
10. 如果把直线x-2y+λ=0向左平移1个单位后,再向下平移2个单位便与圆
x![]() +y
+y![]() +2x-4y=0相切,则实数λ的值是:( )
+2x-4y=0相切,则实数λ的值是:( )
(A) -13或3 (B) 13或-3
(C) 13或3 (D) -13或-3
11. 函数y=sinx,
x∈[![]() ,
,![]() ]的反函数是:( )
]的反函数是:( )
(A) y=arcsinx (-1≤x≤1)
(B) y=π+arcsinx (-1≤x≤1)
(C) y=2π+arcsinx (-1≤x≤1)
(D) y=2π-arcsinx (-1≤x≤1)
12. 轴截面是正方形的一个圆柱的侧面积等于一个球的表面积,那么这个圆柱的体积与这
个球的体积之比等于:( )
(A) 2:3 (B) 3:2
(C) 4:3
(D) ![]()
13. 设P为椭圆上一点,F![]() 、F
、F![]() 中椭圆的两个焦点,若∠PF
中椭圆的两个焦点,若∠PF![]() F
F![]() =75°,∠PF
=75°,∠PF![]() F
F![]() =15°,
=15°,
则椭圆的离心率为:( )
(A)![]() (B)
(B)
![]() (C)
(C) ![]() (D)
(D)
![]()
14. 方程![]() 所表示的曲线是:( )
所表示的曲线是:( )
(A) 圆 (B) 椭圆
(C) 抛物线 (D) 双曲线
15. 设数列 {a![]() } 的前n项和 Sn=2
} 的前n项和 Sn=2![]() -1,
-1,
则 ![]()
![]() 等于:( )
等于:( )
(A) ![]() (B) 1
(B) 1
(C) ![]() (D) 2
(D) 2
二、填空题
16. 不等式![]() >x+1的解集是:( )
>x+1的解集是:( )
(A) { x|![]() ≥x>2 }
(B) { x|-
≥x>2 }
(B) { x|-![]() ≤x≤2 }
≤x≤2 }
(C) { x|![]() >x>2 }
(D)
{ x|-
>x>2 }
(D)
{ x|-![]() ≤x<2 }
≤x<2 }
17. 函数![]() 的单调递减区间是:( )
的单调递减区间是:( )
(A) [ π-![]() ,kπ+
,kπ+![]() ] (k∈Z)
] (k∈Z)
(B) [ kπ+![]() ,kπ+
,kπ+![]() ] (k∈Z)
] (k∈Z)
(C) [ kπ+![]() ,kπ+
,kπ+![]() ] (k∈Z)
] (k∈Z)
(D) [ kπ+![]() ,kπ+
,kπ+![]() ] (k∈Z)
] (k∈Z)
18. 在极坐标系中,经过曲线![]() 的中心,并且和极轴垂直的直
的中心,并且和极轴垂直的直
线的极坐标方程是:( )
(A) ρcosθ=2 (B) ρcosθ=3
(C) ρcosθ=5 (D) ρcosθ=1
19. 用五个1和四个2排成的九位号码中,恰有四个1连在一起的不同号码共
有( )个(用数字作答)
|
20. 要用一块边长为 方形铁片,按下图左将阴影部分裁 下,然后用余下的四个全等的等腰 三角形加工成一个正四棱锥形容器 (如下图右),当所制造的容器的容 积最大时,所裁的等腰三角形底边 长为( )cm. |
三、解答题
21. 已知f(x)是以3为周期的奇函数,若f(1)=1, tga=2,求f(20sinacosa)的
值为:( )
(A) 1 (B) 2
(C) -2 (D) -1
[解析]
22. 已知复数 ![]() 的模为
的模为![]() ,求实数a及复数z的三角形式
,求实数a及复数z的三角形式
[解析]
x=32t![]()
23. 已知抛物线 (t为参数)的焦点为F,A、B、C是抛物线上三点,且点
y=32t
A的纵 坐标是8,如果F恰为△ABC的重心,求BC边所在的直线方程。( )
(A) 4x-y-40=0 (B) 4x+y-40=0
(C) 4x+3y-40=0 (D) 4x-3y-40=0
[解析]
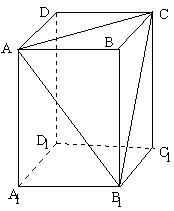
24. 已知正四棱柱
ABCD-A![]() B
B![]() C
C![]() D
D![]() 的底面边长为a,侧棱长为2a(如图),
的底面边长为a,侧棱长为2a(如图),
|
求:(Ⅰ) 点B到平面 AB (A) (C) |
[解析]
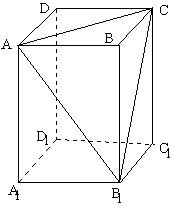
(Ⅱ) 以 B![]() C 为棱,AB
C 为棱,AB![]() C 和 BB
C 和 BB![]() C 为面所成的二面角:(
)
C 为面所成的二面角:(
)
|
(A) (C) |
[解析]
25. 已知函数y=log![]() |1-x|的图象上两点B,C的横坐标分别为a-2,a(a≤0),
|1-x|的图象上两点B,C的横坐标分别为a-2,a(a≤0),
又知A点的坐标为(a-1,0),求△ABC面积的最值及相应的a值。( )
(A)当a=0时,S![]() 有最大值
有最大值![]() (B)当a=1时,S
(B)当a=1时,S![]() 有最大值
有最大值![]()
(C)当a=0时,S![]() 有最小值
有最小值![]() (D)当a=1时,S
(D)当a=1时,S![]() 有最小值
有最小值![]()
[解析]
26. 已知数列{a![]() } 满足条件(n-1)a
} 满足条件(n-1)a![]() =(n+1)(a
=(n+1)(a![]() -1),且a
-1),且a![]() =6,
=6,
令 b![]() =a
=a![]() +n (n∈N).
+n (n∈N).
(Ⅰ) 写出数列{b![]() } 的前四项: ( ),( ),( ),( )
} 的前四项: ( ),( ),( ),( )
[解析]
(Ⅱ) 归纳出数列{b![]() }的通项公式,并给予证明:
}的通项公式,并给予证明:
[解析]
参 考 答 案
一、 1. B 2. A 3. A 4. D 5. A
6. D 7. B 8. C 9. B 10. C
11. C 12. B 13. A 14. D 15. A
二、16. D 17. B 18. D 19. ( 20 ) 20. ( 4 )
三、21. D
[解析] ∵ tga=2 ∴20sinacosa=10sin2a= 10·![]()
∴ f(20sinacosa)=f(8) 又 f(x)是以3为周期的奇函数,且f(1)=1
∴ f(8)=f(3·3-1)=f(-1)=-f(1)=-1 ∴ f(20sinacosa)=-1
22. [解析]
∵ |z|=|![]() ∴
∴ 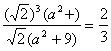
∴ a![]() =3 a=±
=3 a=±![]() 当 a=
当 a=![]() 时
时 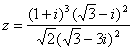
∵ (1+i)![]() 的一个辐角为
的一个辐角为![]()
![]() 的一个辐角为
的一个辐角为![]()
![]() 的一个辐角为
的一个辐角为![]()
∴ 复数z的一个辐角为![]() 此时
此时 ![]()
当![]() 时
时 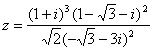
∵ (1+i)![]() 的一个辐角为
的一个辐角为 ![]() 此时
此时![]()
23. B [解析]
消去参数t得到抛物线方程为 y![]() =32x 由已知得A为(2,8),F为(8,0)
=32x 由已知得A为(2,8),F为(8,0)
设D为BC的中点,则D分AF的比为![]() ∴ D点坐标为(11,-4)
∴ D点坐标为(11,-4)
∵ BC过D且被D平分 故可设BC的直线方程为y+4=k(x-11)
y+4=k(x-1)
由方程组 消去x得
y![]() =32x
=32x
ky![]() -32y-32(4+11k)=0 它的两根y
-32y-32(4+11k)=0 它的两根y![]() 、y
、y![]() 即为B、C两点的纵坐标,
即为B、C两点的纵坐标,
∵ D是BC的中点 ∴ ![]() 又由韦达定理得:
又由韦达定理得: ![]()
∴ ![]() k=-4 ∴ BC所在的直线方程为4x+y-40=0
k=-4 ∴ BC所在的直线方程为4x+y-40=0
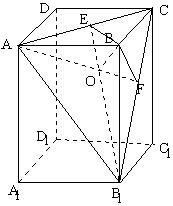
24. (Ⅰ) A
[解析] 作BO⊥平面AB![]() C于O,连结B
C于O,连结B![]() O, 延长后交AC于E,连结BE,
O, 延长后交AC于E,连结BE,
∵ AC⊥BB![]() ,且OB
,且OB![]() 是BB
是BB![]() 在平面AB
在平面AB![]() C上的射影,
C上的射影,
根据三垂线定理的逆定理知AC⊥B![]() E,于是E是正方
E,于是E是正方
形ABCD的中心,∴ ![]() ,
,
|
又∵ BB ∴ 而B |
∴ 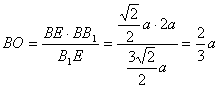
(Ⅱ) A [解析]
连结AO,延长后交B![]() C于F,连结BF,
C于F,连结BF,
∵ B![]() C⊥AB,且AO是AB在平面AB
C⊥AB,且AO是AB在平面AB![]() C上的射影, 根据三垂线定理的逆定理
C上的射影, 根据三垂线定理的逆定理
|
知AF⊥B ∴ BF⊥B |
∴ ![]() ,故
,故![]() ,
,
即平面 AB![]() C 与平面 BB
C 与平面 BB![]() C 相交所成的二面角为
C 相交所成的二面角为![]()
25. C
[解析]
画出函数 y=log![]() |1-x| 的图象,B、C在x轴上的射影为D(a,0),
|1-x| 的图象,B、C在x轴上的射影为D(a,0),
E(a-2.0) 故|ED|=2=2|EA|=2|AD|
S![]() =S
=S![]() -(S
-(S![]() )
)
=![]() (|BE|+|CD|)|ED|-
(|BE|+|CD|)|ED|-![]() [|EA|·|BE|+|AD|·|CD|]
[|EA|·|BE|+|AD|·|CD|]
=![]() |EA|[2(|BE|+|CD|)-(|BE|+|CD|)]
|EA|[2(|BE|+|CD|)-(|BE|+|CD|)]
=![]() |EA|[|BE|+|CD|]=
|EA|[|BE|+|CD|]=![]() [log
[log![]() (3-a)+log
(3-a)+log![]() (1-a)]
(1-a)]
=![]() [log
[log![]() (1-a)(3-a)]=
(1-a)(3-a)]=![]() log
log![]() (a
(a![]() -4a+3)
-4a+3)
=![]() log
log![]() [(a-2)
[(a-2)![]() -1] ∵ a≤0
-1] ∵ a≤0
∴ 当a=0时,S![]() 有最小值
有最小值![]() 无最大值。
无最大值。
26. (Ⅰ) ( 2 ),( 8 ),( 18 ),( 32 )
[解析]
当n=1时,得2(a![]() -1)=0, ∴ a
-1)=0, ∴ a![]() =1,当n=2时,得a
=1,当n=2时,得a![]() =3(a
=3(a![]() -1),
-1),
∵ a![]() =6, ∴ a
=6, ∴ a![]() =3(6-1)=15,当n=3时,得2a
=3(6-1)=15,当n=3时,得2a![]() =4(a
=4(a![]() -1)=4(15-1),
-1)=4(15-1),
∴ a![]() =28. ∴ {b
=28. ∴ {b![]() } 的前四项是 b
} 的前四项是 b![]() =2,b
=2,b![]() =8,b
=8,b![]() =18,b
=18,b![]() =32
=32
(Ⅱ) [解析]
∵ b![]() =2·1
=2·1![]() ,b
,b![]() =2·2
=2·2![]() ,b
,b![]() =2·3
=2·3![]() ,b
,b![]() =2·4
=2·4![]()
∴ 猜想 b![]() =2·n
=2·n![]()