数学理科 模拟试卷八
一、选择题
1. 0.4
，0.4
，0.7三个数的大小关系是：( )
（Ａ） 0.4＜0.4＜0.7
（Ｂ） 0.7＜0.4＜0.4
（Ｃ） 0.4＜0.4＜0.7
（Ｄ） 0.4＜0.7＜0.4
2. 已知
f(x)=3
-3
，则 f
(-2) 的值等于：( )
（Ａ） -1 （Ｂ） 1
（Ｃ） 0 （Ｄ） 0或-1
3. 设α、β是两个平面，直线lα，则“l⊥β”是“α⊥β”的( )
（Ａ） 充分但非必要条件
（Ｂ） 必要但非充分条件
（Ｃ） 充要条件
（Ｄ） 既非充分又非必要条件
4. 已知等差数列
{a
} 中，a
，a
是方程 x
-6x-1=0 的两根，
则 a
+a
+a
+a
+a
等于：( )
（Ａ） 18 （Ｂ） -18
（Ｃ） 15 （Ｄ） 12
|
5. 如图，复平面上的点A、B对应的复数分别是z  ,z ， 设 z （Ａ） a＞0, b＞0 （Ｂ） a＞0, b＜0 （Ｃ） a＜0, b＞0 （Ｄ） a＜0, b＜0 |
6. 把函数y=sin(ωx+φ)(ω＞0, ｜φ｜＜π) 的图象向左平移
个单位，再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得图象的解析式为y=sinx，则：( )
（Ａ） ω=2,φ= （Ｂ）
ω=2,φ=-
（Ｃ） ω=
,φ=
（Ｄ） ω=,φ=
7. 从0，2，4中取出一个数字，再从1，3，5中取出两个数字组成一个无重复数字的
三位数，那么所有不同的三位数共有：( )
（Ａ） 36个 （Ｂ） 48个
（Ｃ） 45个 （Ｄ） 54个
8. 在三棱锥A—BCD中，AB=CD=2，E、F分别是AC、BD的中点，且EF=
，
则AB与CD所成的角为：( )
（Ａ） 30° （Ｂ） 60°
（Ｃ） 90° （Ｄ） 120°
9. 当x∈[-1,0]时，下列式子的值等于π的是：( )
（Ａ） arccos(-x)+arcsin 
（Ｂ） arccos(-x)+arccos
（Ｃ） arcsinx+arccos
（Ｄ） arccosx+arcsin
10. 
(x∈R,x≠0)的展开式中，实数项的系数和为：( )
（Ａ） -2
（Ｂ） 2
（Ｃ） 2
（Ｄ） 0
11. 
的半径和圆心坐标分别为：( )
（Ａ） 2，(2， )
（Ｂ） 2，(2，- )
（Ｃ） 1，(1，- )
（Ｄ） 1，(1， )
12. 圆锥曲线 3x-y-6x-4y+2=0 的焦点坐标是：(
)
（Ａ） (1，0)，(1，-4)
（Ｂ） (3，-2)，(-1，-2)
（Ｃ） (1+
，-2)，( 1-，-2)
（Ｄ） (1，-2+)，(1，-2-)
13. 对任意x∈R，函数f(x)表示-x+3，
x+，x-4x+3 中的较大者，
则f(x)的最小值是：( )
（Ａ） 2 （Ｂ） 3
（Ｃ） 8 （Ｄ） -1
14. 设f(x)=asin(πx+α)+bcos(πx+β)+4，其中a,b,α,β∈R，且ab≠0, a≠kπ，
(k∈Z)若f(1995)=5，则f(1996)等于：( )
（Ａ） 1 （Ｂ） 2
（Ｃ） 3 （Ｄ） 5
15. 动点M到定点A(1，1)的距离减去点M到定点B(1，-1)的距离的差是非负实数a
(定值)，则动点M的轨迹是：( )
（Ａ） 双曲线的一支
（Ｂ） 双曲线的一支或一条直线
（Ｃ） 双曲线的一支或一条直线或一条射线
（Ｄ） 除(C)外还有别的情形
二、填空题
16. 已知集合
A={ x｜
＜0 }, B={ x｜2x+mx+n≤0}A∪B=R，
若A∩B={x｜3＜x≤4}，则m+n=( )
（Ａ） 14 （Ｂ） -14
（Ｃ） 
（Ｄ） 7
17. 函数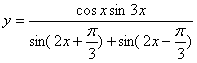 
的最小正周期为π，值域是：( )
（Ａ） (-，
)
（Ｂ） (，)
（Ｃ） (-，-)
（Ｄ） (-，)
18. 已知数列 {a} 的前n项和 S=2
，则 
的值是：( )
（Ａ） （Ｂ）
（Ｃ） （Ｄ） -
19. Rt△ABC中，AB=AC=1，用点C为一个焦点作一个椭圆，使这个椭圆的另一个焦点在AB
边上，椭圆过A、B两点，则这个椭圆的焦距长为：( )
（Ａ） -
（Ｂ） 
（Ｃ） 
（Ｄ）
20. 现要制作一个底面半径为4cm，母线长为6cm的圆锥，用一块长方形材料来做它的侧
面，这样的长方形材料的最小长与宽分别为( )cm 和( )cm。
三、解答题：
21.已知复数z=(1-cosθ+isinθ)
,其中θ ∈(0,
),求argz及｜z｜($S*D$)。
（Ａ）argz=
,｜z｜=32sin 
（Ｂ）argz=
,｜z｜=32sin 
（Ｃ）argz=
,｜z｜=32sin （Ｄ）argz=
,｜z｜=32sin
[分析解答]
22. 已知函数
，
(1) 求f(x)的定义域；（ ）
（Ａ） (-120,0)∪(0,+∞) （Ｂ） (-∞,0)∪(0,+120)
（Ｃ） (-∞,+∞) （Ｄ） (-∞,0)∪(0,+∞)
[分析解答]
(2) 判断f(x)的奇偶性，并说明理由；
[分析解答]
(3) 设函数
, x∈(0,+∞),求g (x)。（ ）
（Ａ）
,x∈(,-∞) （Ｂ）
,x∈(,+∞)
（Ｃ）
,x∈(,+∞) （Ｄ）
,x∈(,+∞)
[分析解答]
|
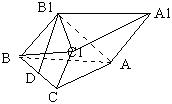
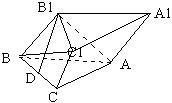
23. 已知斜三棱柱ABC—A1B1C1的底△ABC为直角三角形，∠C=90°；侧棱与底面成60°角， B1点在底面射影D为BC中点。
(1) 求证AB1⊥BC1； |
[分析解答]
(2) 若侧面A1ABB1与C1CBB1成30°的二面角，BC=2cm，求四棱锥A—B1BCC1的体积。（ ）
|
（Ａ）  （Ｂ）  （Ｃ） |
（Ｄ） 
[分析解答]
24. 有一种大型商品，A、B两地都有出售，且价格相同，某地居民从两地之一购得商品后回运的费用不同，已知每单位距离A地的运费是B地运费的3倍，且A、B两地距离为10km，顾客选择A或B地购买这件商品的原则是，包括运费和价格的总费用较低。求A、B两地的售货区域的分界线的曲线形状，并指出在曲线上、曲线内、曲线外的居民应如何选择购货地点。( $S*D$ )
（Ａ）圆C内的居民应从B地购货，圆C外的居民应选择A地购货；圆C上的居民可任意。
（Ｂ）圆C内的居民应从A地购货，圆C外的居民应选择A地购货；圆C上的居民可任意。
（Ｃ）圆C内的居民应从B地购货，圆C外的居民应选择B地购货；圆C上的居民可任意。
（Ｄ）圆C内的居民应从A地购货，圆C外的居民应选择B地购货；圆C上的居民可任意。
[分析解答]
25. 已知n∈Z
且n≥2，a＞1，求证
[分析解答]
26. 设F是椭圆
的左焦点，M是C1上任意一点，P是线段FM
上的点，且满足条件：｜FM｜:｜MP｜=3:1，求点P的轨迹C2。
[分析解答]
参 考 答 案
一、
1. C 2. C 3. A 4. C 5. D
6. B 7. B 8. B 9. D 10. A
11. C 12. A 13. A 14. C 15. D
二、
16. B 17. D 18. C 19. D 20. ( 12 )( 9 )
三、
21. D
[分析解答] ∵1-cosθ+isinθ =2sin +2isin cos
=2sin [cos(
-)+isin(-)]
∵θ∈(0,),∴ ∈(0,
) ∴ sin ＞0，
∴z=32sin [cos()+isin()]
∵sin ＞0, ∴｜z｜=32sin
又∵2π＜＜
,
∴0＜ -2π=＜,
∴argz= -2π=
∴argz=,｜z｜=32sin
22. (1) B
[分析解答]
令2 -1≠0, ∴2≠1, ∴x≠0
∴f(x)定义域为(-∞,0)∪(0,+∞)
(2) [分析解答]
任取x∈(-∞，0)∪(0,+∞),则-x∈(-∞,0)∪(0,+∞)
∵f(x)-f(-x)=x(
)
∴f(x)=f(-x) ∴f(x)是偶函数。
(3) C [分析解答]
由已知g(x)=
,x∈(0,+∞) ∴ 
,x∈(0,∞)
令y=g(x), ∵ 
≠0,∴y≠, ∴ 
∴2y2-2y=2+1 ∴
(2y-1)2=2y+1
∵y≠,2y-1≠0 ∴ 2=
∵x＞0,
∴2＞1
∴ ＞1, ∴ 
＞0, ∴y＞
∴ 
,
∴ 
,x∈(,+∞)
23. (1) [分析解答]
证明：连B1D，∵D是B1在底面ABC上的射影，∴B1D⊥平面ABC。
∵AC在平面ABC内，∴B1D⊥AC 又∵∠C=90°，BC⊥AC
B1D∩BC=D,B1D、BC平面BC1 ∴AC⊥平面BC1
连B1C,∴B1C是AB1在平面BC1上的射影。
又∵∠B1BD是侧棱B1B与底面所成角
∴∠B1BD=60°，而∠B1DB=90°，
∴BD=
B1B ∵D是BC中点，BD=BC,
∴B1B=BC,∴B1BCC1是菱形 ∴ BC1⊥ B1C, ∴ BC1⊥AB1
(2) B
[分析解答]
∵BC=BB1=2cm,∠B1BC=60°
∴ S
_·BC·sin60°=
取BB1中点M，连MC，MA，
∴BM=1cm,CM=BM+BC -2BM·BCcos60°=3
∴CM+BM=BC，∴∠BMC=90° ∴BB1⊥MC
又由(1)AC⊥平面BCC1B1,∴AC⊥BB1，
又∵AC∩MC =C, AC、MC在平面MAC内，∴BB1⊥平面MAC，
∴BB1⊥AM
∴∠CMA为侧面A1ABB1与C1CBB1所成二面角的平面角，
∴∠CMA=30°,又∵∠ACM=90°，∴AC=CMtg30°=1cm
∴V
= 
·
·1=
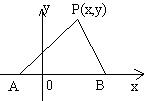
24. D [分析解答]
|
以A、B所在直线为x轴，A、B中点O为坐标原点，建立如图直角坐标系。 ∵｜AB｜=10,∴点A(-5,0),B(5,0) 设某地P的坐标为(x,y)，并设A地运费为3a元/公里， 则B地运费为a元/公里，设P地 |
居民购货总费用满足条件(P地居民选择A地购货)：
价格+A地运费≤价格+B地运费
即
≤a 
∵a＞0,∴
≤
两边平方，整理得：
≤
∴以
为圆心，
为半径的圆是A、B两地购货区域的分界线。
圆C内的居民应从A地购货，圆C外的居民应选择B地购货；圆C上的居民可任意选择。
25. [分析解答]
证明：(1)当n=2时，左式
∵a＞1＞0,∴a+
＞2 (Ι)(∵a≠)
又∵a＞1,∴＜1,∴a＞,∴a-＞0,
(Ι)式两边同乘以a-，得：
,
∴当n=2时，不等式成立。
(2)假设当n=k(k∈N且k≥2)时，
＞k(
)成立
∴ 
＞(k+1)( )
又∵
∵a＞1,∴a
＞1,a
＞1(∵k∈N)
∴a-1＞0,a-1＞0,a-1＞0,a＞0
∴a
＞
∴a＞(k+1)(a-)成立
∴当n=k+1时，不等式成立。
由(1)和(2)，对任意n∈N且n≥2，不等式均成立。
26. [分析解答]
(1)由椭圆C1的方程，得C1中心为(,0),a=3,
,左焦点F(-1,0)
∵｜FM｜:｜MP｜=3:1，P是线段FM上的点，∴P为FM的内分点，∴FP:PM=2:1，
∴定比λ=2.设P(x,y),M(xO,yO)
xO=+3cosθ (θ
为参数)
∵M在椭圆C1上，∴
yO=
∴
消去θ ，得
，即为轨迹C2的方程，∴ C2为椭圆
(2) ∵C2的左焦点F(-1,0)与C1的左焦点重合，以F为极点，射线Fx为极轴建立极坐标系。
∵
,
∴ C1的极坐标方程为
,
C2的极坐标方程为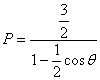
∴｜CD｜=PD-PC=
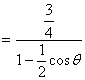
｜AB｜=PA-PB=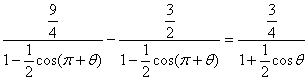
∵｜CD｜=2｜AB｜
∴
∴cosθ=,
∴ 
设直线l的斜率为K,∴K=±
∴l的方程为
(注：文科考生(1)不用参数方程求解，此处解略)