高一物理功和功率单元试题

第七章 机械能 功和功率单元测试

一、选择题

1、关于重力势能，以下说法中正确的是（　 ）

A. 某个物体处于某个位置，重力势能的大小是唯一确定的

B. 重力势能为０的物体，不可能对别的物体做功

C. 物体做匀速直线运动时，重力势能一定不变

D. 只要重力做功，重力势能一定变化

2 、在h高处，以初速度v₀向水平方向抛出一个小球，不计空气阻力，小球着地时速度大小为（　 ）

A. 　　　B. 　　 C. 　　 D.

3、 一质量为 m的小球，用长为l的轻绳悬挂于O点。小球在水平拉力F作用下，从平衡位置P点很缓慢地移动到Q点，如图1所示，则拉力F所做的功为（　 ）

A. mglcosθ　　　 B. mgl(1－cosθ)　　　C. Flcosθ　　　D. Flθ

4、 如图2所示，固定在地面上的半圆轨道直径ab水平，质点P从a点正上方高H处自由下落，经过轨道后从b点冲出竖直上抛，上升的最大高度为H，空气阻力不计．当质点下落再经过轨道a点冲出时，能上升的最大高度h为(　)

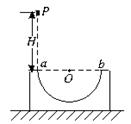
图2

　　A．h＝H　　　　　　　　　　　　　　　 B．h＝

　　C．h＜　　　　　　　　　　　　　　　 D．＜h＜H

5、 质量为m的物体静止在粗糙的水平地面上，若物体受水平力F的作用从静止起通过位移s时的动能为E₁，当物体受水平力2F作用，从静止开始通过相同位移s，它的动能为E₂，则：

　　A. E₂＝E₁　　　　　　　　　　　　　　　　B. E₂＝2E₁

　　C. E₂＞2E₁　　　　　　　 　　　　　　　　D. E₁＜E₂＜2E₁

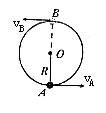
 6、 质量为m的小球被系在轻绳的一端，在竖直平面内做半径为R的圆周运动，运动过程中小球受到空气阻力的作用。设某一时刻小球通过轨道最低点，此时绳子的张力为7mg，此后小球继续做运动，经过半个圆周恰能通过最高点，则在此过程中小球克服空气阻力做的功为：

　　

　　

二、填空题

7、 如图3：质量为m的小球从位置A运动到位置B的过程重力所做的功_____J．

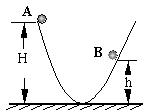
8、将物体以60 J的初动能竖直向上抛出，当它上升至某点P时，动能减少为10J，机械能损失10 J，若空气阻力大小不变，则物体落回抛出点时的动能为_____J．

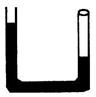9、如图4所示，粗细均匀的U形管底边宽10cm，两边液柱高分别为25cm与5cm，当将右端塞子打开时左侧液体将向右流动，若一切摩擦不计，则液体流动的最大速度大小等于______________m/s。

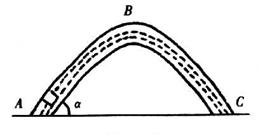
10、如图5所示，AB与CD为两个斜面，分别与一个光滑的圆弧形轨道相切，圆弧的圆心角为，半径为R，质量为m的物块在距地面高为h的A处无初速度滑下，若物块与斜面的动摩擦因数为，物体在斜面上(除圆弧外)共能运动的路程_____m.

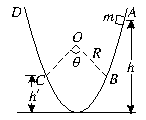
图5

11、一架喷气式飞机的质量为5.0×10³kg，起飞过程中受到的牵引力为1.8×10⁴N，受到的阻力是飞机机重的0.020倍，起飞速度为60m/s，起飞过程中滑跑的距离_____m.

三、计算题

12、如图6所示，斜面倾角为 ，质量为m的滑块距挡板P为s，以初速度v沿斜面上滑，滑块与斜面间的动摩擦因数为 ，滑块所受摩擦力小于滑块重力沿斜面的分力，若滑块每次与挡板相碰均无机械能损失，求滑块经过的路程有多大？

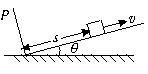
图6

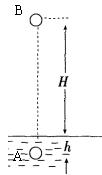
13、物体从高出地面的B处由静止自由落下，不考虑空气阻力，落至沙坑表面后又进入沙坑并在A处停止（如图7）。求物体在沙坑中受到的平均阻力是其重力的多少倍。

14．一封闭的弯曲玻璃管处于竖直平面内，其中充满某种液体，内有一个密度为液体宇航局度的木块，从管的A端由静止开始运动，木块与管壁间动摩擦因数μ=0.5，管两臂长AB=BC=L=2m，顶端B处为一小段光滑圆弧，两臂与水平面成α=37°角，如图8所示，求：

（1）木块到达B点时的速度。

（2）木块从开始运动到最终静止通过的路程。

15　如图9所示，一个质量为m的圆环套在一根固定的水平直杆上，，环与杆的动摩擦因数为μ，现给环一个向右的初速度v₀，如果在运动过程中还受到一个方向始终竖直向上的力F的作用，且（k为常数，v为环的运动速度），试讨论环在整个运动过程中克服摩擦力所做的功（假设杆足够长）。

参考答案

1、解析　由重力势能的表达式E_p=mgh可知，由于高度h具有相对性，重力势能的大小也具有相对性，即处于某个位置的某个物体，在选择不同的参考平面时，重力势能的大小是不同的。

重力势能的大小具有相对性，其大小与参考平面的选取有关，所以重力势能为０的物体，是指物体处于参考平面上，并不能表明物体不具有做功的本领。如在地面上流动的一薄层水，若取地面为参考平面，则其重力势能为０，但当这些水流向更低处时仍可对别的物体做功。

物体的重力势能是由物体的重力和物体的高度共同决定的，只要物体的高度发生变化，物体的重力势能就一定发生变化。例如，当物体沿斜面匀速下滑时，高度减小，重力势能将减小。

重力的方向总是竖直向下的，重力做功时物体的高度肯定发生变化，重力势能也一定发生变化。

可见，正确选项为D。

2、解析  在小球下落的整个过程中，对小球应用动能定理，有

　 ，

解得小球着地时速度的大小为　 。

正确选项为C。

3、解析  小球受重力、水平拉力和绳子拉力的作用，其中绳子拉力对小球不做功，水平拉力对小球做功设为W，小球克服重力做功mgl(1－cosθ)。小球很缓慢移动时可认为动能始终为0，由动能定理　　　　　　　  W－mgl(1－cosθ)=0，

可得　　　　　　　　　　　　　   W= mgl(1－cosθ)。

正确选项为B。

4、解析：质点P第一次通过半圆弧的速率大于第二次通过半圆弧的速率，则第一次通过圆弧的压力和摩擦力均大于第二次．则第一次物体克服摩擦力做功W_f1大于第二次克服摩擦力做功W_f2，根据动能定理，有

　　W_f1＝mg(H-H)

　　W_f­₂＝mg(H-h)

　　因为W_f1＞W_f2，则

　　mg(H-H)＞mg(H-h)，得h＞

　　因为W_f2＞0，则h＜H．

　　故＜h＜H，故选项D正确．

　　答案：D

5、解析：正确答案为C。解答本题的关键是弄清物体运动过程中受到哪些力和各力做功情况（正功还是负功或不做功），然后由动能定理分析判断。

　　物体在粗糙的水平面上通过位移s的过程中，所受到的摩擦力不变，由动能定理可得：

　　

　　

　　

　　注意：此题列动能定理方程时，易漏掉摩擦阻力的功，误认为Fs是合外力所做的功。

6、解析：小球从最低点到最高点通过这半个圆周的过程中，空气阻力大小未知，方向始终与速度方向相反，是变力。求此变力所做的功应从功和能的关系入手，由动能定理求出，但先应分别求出小球在最低点和最高点的动能。

　　如图所示，小球在最低点A时，由牛顿第二定律得：

　　

　　小球在最高点B时，由牛顿第二定律得：

　　

　　小球从A经半个圆周运动到B的过程中由动能定理

　　

　　

　　

7、解析：由于重力做功与通过的路径无关，只决定于物体的重力mg和物体初末位置的高度差，所以物体由A位置运动到B位置。虽然先运动到地面高度再回到B高度，但初末位置的高度差是H—h，那么重力做的功就是W＝mg（H—h）。

8、解析：物体动能的减少是重力与阻力对物体做负功而引起的，由题意知，ΔE_k＝50 J＝W_G＋W_f，而W_f＝10 J故W_G＝40 J，又因二者作用位移相同，故＝，物体上升到最高点的过程中阻力做功为W_f′由动能定理，0-60 J＝-5 W_f′，即W_f′＝12 J，而下落过程中阻力做功的值仍为W_f′＝12 J，对全过程(上升与下落)应用动能定理，有E_k′-60＝-2 W_f′，故E_k′＝60-2×12 J＝36 J．

答案：36

9、解析：管中的液体在流动过程中各部分速率是相等的，而且，当两管中液面相平时，其速率最大，设单位长度液体的质量为m，根据动能定理：

，∴v=0.7m/s。

10、解析：物块在斜面AB和CD上往复运动，摩擦力的方向不断变化，由于摩擦阻力做功，物块每次上滑的最高点不断在降低，当物体在B点或C点速度为零时，便在光滑曲面上往复运动，高度不再变化．

　　设物块在斜面上(除圆弧外)运动的总路程为s，以A为初位置，B或C为末位置，取全过程研究，由动能定理，有W_G＋W_F＝0

　　即mg(h-h′)-mgscos＝0

　　s＝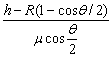

　　答案：［h-R(1-cos/2)］/cos/2

11、解析：以飞机为研究对象，起飞过程中受力分析如图，

F_f＝kmg＝0.02×5.0×10³×10N=1000N

根据动能定理得到

F L－F_f L＝－0

由此可得：L＝=＝5.3×10²m

12．解析：由于滑块重力沿斜面向下的分力大于滑块所受摩擦力，所以可断定滑块最终将停靠在挡板处．从以v向上滑动至最终停下，设滑块经过的路程为l，则重力做正功，摩擦力做负功．

　　解法一：此过程重力对滑块做功W_G＝mgssin ，

　　摩擦力做功W_f＝- mglcos

　　对滑块由动能定理，有：

　　mgssin - mglcos ＝0-mv²

解得l＝

13解析：解法一：选物体为研究对象，先研究自由落体过程，只有重力做功，设物体质量为m，落到沙坑表面时速度为v，根据动能定理有

　　　　　　　　　　　 ①

再研究物体在沙中的运动过程，重力做正功，阻力 做负功，根据动能定理有

　　　　　　　　  ②

由①②两式解得

可见物体在沙坑中受到的平均阻力是其重力的倍。

解法二：研究物体运动的全过程，根据动能定理有

解得

可见物体在沙坑中受到的平均阻力是其重力的倍。

（1）若物体的运动过程包含几个不同的物理过程，用动能定理解题时可以分段列方程，然后联立求解。也可以视全过程为一整体列方程求解。当既能用“分段法”求解，又能用“整体法”求解时，一般来说，整体法要比分段法简捷。

（2）该题也可用牛顿第二定律和运动学公式求解：先研究自由下落过程，根据自由落体运动规律，物体到达沙坑表面时的速度为

再研究物体在沙坑中的运动过程，物体受重力和阻力 作用，设物体运动加速度为a，选竖直向下为正方向，根据牛顿第二定律有

mg－F_μ =ma

根据匀减速运动的公式有

以上三式联立解得

点拨：将这种解法与前两种解法相比较，可以看出应用动能定理（特别是用整体法）比较简便。一般来说，对于做直线运动或曲线运动，恒力或变力做功过程中，涉及速度和位移，不直接涉及加速度和时间的问题，选用动能定理解题比较简捷。

14．解析：（1）木块所受浮力

管壁对木块支持力

（2）木块最终只能静止在B处

15、解析　 对于环在整个运动过程中克服摩擦力所做的功，可分下列三种情况进行讨论：

　（1）若，则环与杆之间无弹力，也就无摩擦力，环始终做匀速直线运动，克服摩擦力做功为零。

　　（2）若，则环先在摩擦力的作用下做减速运动，当速度减小到，环受到摩擦力为零，以后环的速度不再改变，环做匀速直线运动，根据动能定理环克服摩擦力所做的功为。

　（3）若，则在摩擦力作用下做减速运动，直至环停止运动，所以环克服摩擦力所做的功的大小为　。

点拨　本题为开放性问题，寻求开放点是解决此类问题的关键，而本题的开放之处在于环的初速度的大小的不确定性，从而导致了环与杆间的压力的大小与方向的不确定性。