高三第一轮复习数学---圆锥曲线的综合应用(2)
一、教学目标:进一步巩固用圆锥曲线的定义和性质解决有关应用问题的方法.
二、教学重点:巩固用圆锥曲线的定义和性质解决有关应用问题的方法.
三、教学过程:
(一)主要知识:
(二)例题分析:
[例1](2001全国高考)已知抛物线![]() 的弦
的弦![]() 过抛物线的焦点,
过抛物线的焦点,![]() 点在抛物线的准线上,
点在抛物线的准线上,![]() 轴,
轴,
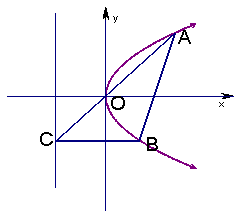 证明:直线
证明:直线![]() 过原点。
过原点。
(目的:进一步探讨抛物线的几何性质)
【解析】利用方程求解
因为抛物线![]() 的焦点坐标是
的焦点坐标是![]() 设直线
设直线![]() 的方程是:
的方程是:![]() 代入抛物线方程得:
代入抛物线方程得:![]() ,设
,设![]() ,则
,则![]() 点坐标为
点坐标为![]()
则![]() 因为
因为![]() 轴,
轴,![]() 点在抛物线的准线上,直线
点在抛物线的准线上,直线![]()
的斜率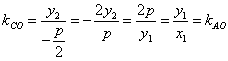 ,所以直线
,所以直线![]() 过原点。
过原点。
(解法二)向量法
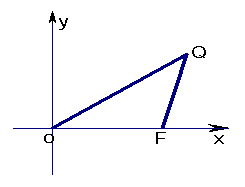
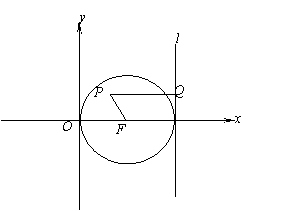 [例2]如图,垂直于x轴的直线l于与圆F:
[例2]如图,垂直于x轴的直线l于与圆F:![]() 相切,P为坐标平面内一动点,PQ⊥l于Q,且
相切,P为坐标平面内一动点,PQ⊥l于Q,且![]() .
.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)过圆心F作直线交点P的轨迹于A、B两点,
若![]() , 求点A、B的坐标.
, 求点A、B的坐标.
(目的:综合运用直线、圆、椭圆的几何性质解决相关问题)
【解析】
(Ⅰ)由条件,![]()
设点![]()
![]() 化简得
化简得
所以,![]() 即为所求点
即为所求点![]() 的轨迹方程。
的轨迹方程。
(Ⅱ)设过![]() 的直线方程为
的直线方程为![]() ,因为
,因为![]()
可知![]() 存在,且有
存在,且有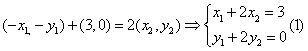
又有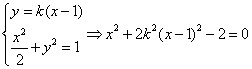 即
即![]()
且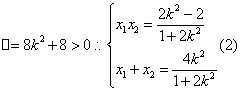 由(1),(2)
由(1),(2)
得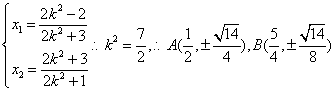
[例3]已知![]() 的面积为
的面积为![]() ,且
,且![]() 建立如图所示的直角坐标系。
建立如图所示的直角坐标系。
(I)若![]() 求向量
求向量![]() 所在的直线方程;
所在的直线方程;
(II)设![]() 若以
若以![]() 为中心、
为中心、![]() 为焦点的椭圆经过点
为焦点的椭圆经过点![]() ,求当
,求当![]() 取得最小值时,椭圆的方程。
取得最小值时,椭圆的方程。
(目的:综合运用函数的性质、向量、导数的有关知识、方法解决问题)
【解析】
 (I)设
(I)设![]()
![]()
![]()
![]()
![]() 所在的直线方程为
所在的直线方程为![]() 或
或![]() 。
。
(II)![]()
又![]()
令![]() 则
则![]() 在
在![]() 上递增,
上递增,![]() 此时
此时![]() 取最小值,
取最小值,![]()
由题意,设椭圆方程![]()
[例4]已知:![]() 面积为
面积为![]() 以O为中心,F为焦点的双曲线过点P。
以O为中心,F为焦点的双曲线过点P。
(I)求![]() 的大小;
的大小;
(II)若P点到中心O的距离为P点到两焦点距离的比例中项,请建立恰当的坐标系,写出双曲线的方程
【解析】
设![]()
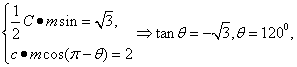 即
即![]()
(2)以O为坐标原点,OF所在直线为![]() 轴建立直角坐标系,设双曲线方程为
轴建立直角坐标系,设双曲线方程为![]() 点关于O的对称点为
点关于O的对称点为![]() ,
,![]() 则据题知:
则据题知:![]() 由(1)得
由(1)得![]() (1),又
(1),又![]()
![]()
![]()
![]()
![]() 即
即![]()
![]()
![]()
![]()
![]() 由(1),(2),(3)可得
由(1),(2),(3)可得![]()
![]() 所以曲线方程为
所以曲线方程为![]()
(三)巩固练习:
1.以过椭圆的右焦点的弦为直径的圆与其右准线的位置关系为 ( )
(A)相交 (B)相切 (C)相离 (D)不能确定
(目的:理解并引申以过焦点弦为直径的圆与圆锥曲线相应准线的位置关系)
【答案】(C)
【解析】利用椭圆的第二定义及离心率小于![]() 的特性。
的特性。
2.双曲线![]() 的离心率
的离心率![]() ,焦点到其中一条渐进线的距离为
,焦点到其中一条渐进线的距离为![]() ,
,![]() 是双曲线上关于
是双曲线上关于![]() 轴对称的两点,
轴对称的两点,![]() 为坐标原点,则
为坐标原点,则![]() 等于( )
等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(目的:掌握等轴双曲线的离心率、渐进线的特征及其对称性)
【答案】(A)
【解析】由![]() 得
得![]() 由焦点到渐进线的距离为2,得
由焦点到渐进线的距离为2,得![]() 故双曲线的方程为
故双曲线的方程为![]() 设
设![]() 则
则![]() ,
,![]()
3.抛物线![]() 的动弦
的动弦![]() 长为
长为![]() ,则
,则![]() 中点
中点![]() 到
到![]() 轴的最短距离是( )
轴的最短距离是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(目的:理解并掌握抛物线的定义)
【答案】(D)
【解析】![]() 利用抛物线的定义可得。
利用抛物线的定义可得。
4.已知椭圆![]() ,
,![]() 为左焦点,
为左焦点,![]() 为左顶点,
为左顶点,![]() 为上顶点,
为上顶点,![]() 为下顶点,且
为下顶点,且![]() 则椭圆的离心率为
则椭圆的离心率为![]() 。
。
(目的:掌握利用条件列出![]() 的关系,从而求出离心率)
的关系,从而求出离心率)
【答案】![]()
【解析】
![]() 解出
解出![]() 。
。
5.双曲线![]() 的中心在原点,以坐标轴为对称轴,并且与圆
的中心在原点,以坐标轴为对称轴,并且与圆![]() 的一个交点为
的一个交点为![]() ,如果圆在
,如果圆在![]() 点的切线与
点的切线与![]() 的渐进线平行,则
的渐进线平行,则![]() 的方程是
的方程是![]() 。
。
(目的:利用渐进线求双曲线方程)
【答案】![]()
【解析】圆![]() 在
在![]() 点的切线方程为
点的切线方程为![]() ,
,
设![]() 的方程为
的方程为![]() 过点
过点![]()
![]()
四、小结:
1、与圆锥曲线的几何性质相关的问题有“中点弦”问题、对称性问题、最值问题等,若条件和结论能明显体现几何特征及意义,则考虑用图形性质来解决;若条件和结论能明显体现一种明确的函数关系,则可考虑先建立目标函数,再利用求最值常用的配方法、判别式法、不等式法及函数的单调性法。
2、 解析几何也可以与数学的其他知识想联系,例如与向量知识相联系是一个主要的趋势,这时在解题时,要能够顺利地实现一知识向另一知识的转化。
五、作业: