高二年级物理电磁感应周练题

高二年级物理电磁感应周练题

班级　　　　姓名　　　　 学号　　   日期：

一、选择题（5*8=40）　　　　　　　　　　　　　　　　　　　 

1、下列几种说法中正确的是　　(　 )

A．线圈中磁通量变化越大，线圈中产生的感应电动势一定越大

B．线圈中磁通量越大，产生的感应电动势一定越大

C．线圈放在磁场越强的位置，产生的感应电动势一定越大

D．线圈中磁通量变化越快，线圈中产生的感应电动势越大

第5题

（第4题）

2、如图所示，在竖直向下的匀强磁场中，将一水平放置的金属捧ab以水平初速度vo抛出，设在整个过程中金属捧的方向不变且不计空气阻力，则在金属棒运动过程中产生的感应电动势大小变化情况是(　　)

A　越来越大　　

B　越来越小

C　保持不变　　

D　无法判断

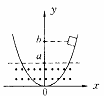
3、光滑曲面与竖直平面的交线是抛物线。如图所示，抛物线的方程其下半部处在一个水平方向的匀强磁场中、磁场的上边界足Y=a的直线(图中的虚线所示)一个小金属块从抛物线Y=b(b＞a)处以速度v沿抛物线下滑。假设抛物线足够长，则金属块在曲面上滑动的过程中产生的焦耳热总量是（　　）

A、 mg(b-a)+ 　　　　　　　 B 、

C 、mgb　　　　　　　　　　　　  D 、mg(b-a)

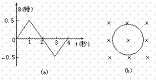
4、如图所示，圆形线圈垂直放在匀强磁场里，第1秒内磁场方向指向纸里，如图（b）．若磁感应强度大小随时间变化的关系如图 （a），那么，下面关于线圈中感应电流的说法正确是：(　　 )

A．在第1秒内感应电流增大，电流方向为逆时针

B．在第2秒内感应电流大小不变，电流方向为顺时针

C．在第3秒内感应电流减小，电流方向为顺时针

D．在第4秒内感应电流大小不变，方向为顺时针

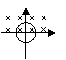5、一圆形线圈，一半置于匀强磁场中，磁场方向垂直纸面向里，如右图所示。

为使线圈中感应出顺时针方向的电流，应使线圈（　　 ）

 A、沿+x方向平动　　　　　　　　 B、沿x轴转动90°

 C、沿+y方向平动　　　　　　　　 D、绕y轴转动90°

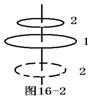6、如图16-2，一水平放置的圆形通电线圈1固定，从上向下看电流方向为逆时针方向，另一较小的圆形线圈2从线圈1的正上方下落，在下落过程中两线圈平面始终保持平行且共轴，则线圈2从线圈1的正上方下落至线圈1的正下方过程中，从上往下看，线圈2中的感应电流应为（　　）

A、 无感应电流　　　　　 B、有顺时针方向的感应电流

C、 先是顺时针方向，后是逆时针方向的感应电流

D、先是逆时针方向，后是顺时针方向的感应电流

题号	1	2	3	4	5	6
答案

二、填空题（4+6）

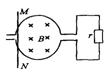
9、如右图所示，长为L的导线下悬一小球，在竖直向上的匀强磁场中做圆锥摆运动，圆锥的偏角为　 ，摆球的角速度为　 ，磁感应强度为B，则金属导线中产生的感应电动势大小为__________

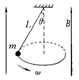
10、如图所示，导线全部为裸导线，半径为R米的圆内有垂直于圆平面的匀强磁场，磁感应强度为　 B特斯拉，一根长度大于2R的导线MN以速率V在圆环上无摩擦地自左端匀速滑动到右端，电路的固定电阻为r欧姆，其余电阻忽略不计，在MN滑动过程中通过电阻r上的电流强度的平均值为________安培，当MN从圆环的左端滑到右端时通过r的电量为_______库．

　　　　　　　　　　　　 （第9题）　　　　　　　　　　　　　　  （第10题）

三、计算题（12+12+13+13）

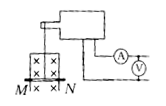
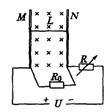11、MN为竖直放置的平行金属杆，两杆相距20cm，两杆间匀强磁场方向垂直纸面向里，导体捧L可沿杆无摩擦地滑动，整个装置如图所示，导体棒L的质量为72g，电阻为1欧，电阻Ro=8欧，电压U＝36V，当可变电阻调到8欧时，导体棒L刚好静止，求：(1)匀强磁场磁感应强度B的大小。(2)如果可变电阻R短路，导体棒L向什么方向运动？

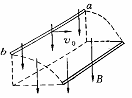
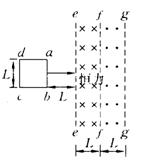12、两个沿竖直方向的磁感应强度大小相等、方向相反的匀强磁场穿过光滑的水平桌面。它们的宽度为L，一个质量为m、边长为L的平放在桌面上的正方形线圈的ab边与磁场边界ee′的距离为L如图所示。线圈在恒力作用下由静止开始沿桌面加速直线运动。ab边进入左边的磁场时恰好做速度为v的匀速直线运动。求：(1)当ab边刚越过ff′时线圈的加速度．(2)当ab边运动到ff′gg′之间的正中间位置时．线圈又恰好做匀速直线运动．从ab边刚越过ee′到达有磁场正中间位置的过程中，线圈共产生多少热量?

13、电动机牵引一根原来静止的、长L=1 m 、质量m=0.1kg的导体棒R=1Ω，竖直轨道处于B=1T的磁场中，当棒由静止上升h=3.8m时获得稳定的速度，该过程回路共产生14J的热量。电压表和电流表的示数分别为7V和1A。电动机内阻为1Ω，g=10m/s².求：（1）棒能达到稳定的速度？（提示：此时拉力功率等于重力和安培力功率之和）（2）棒由静止到稳定所需要的时间？

14、如图，abcd和abcd为在同一竖直平面内的金属导轨，处在磁感应强度为B的匀强磁场中，磁场方向垂直导轨所在的平面（纸面）向里。导轨的a b段与a b段是竖直的，距离为L； c d段与c d段也是竖直的，距离为L。x y与x y为两根用不可伸长的绝缘轻线相连的金属细杆，质量分别为m 和m ，它们都垂直于导轨并与导轨光滑接触。两杆与导轨构成的回路的总电阻R，F为作用于金属杆x y上的竖直向上的恒力。已知两杆运动到图示位置时，已匀速向上运动，求此时作用于两杆的重力的功率的大小和回路电阻上的热功率。

答案

1．D　2.C　　3.A　4.B　　5.BD　　 6.C

9.　 E=B(Lsin＠)²w

10.  B∏Rv/2r;　b∏R²/r

11.　 1T;　 向上运动

12.　 3v²/2L;　39/32mv²