高二年级物理同步辅导讲座之九
北 京 四 中
年 级：高 二 科 目：物 理 期数：0109
编 稿：陈素玉 审 稿：厉璀琳 录入：刘红梅
教学内容：查理定律，热力学温标，理想气体的状态方程
教学目标：1、掌握查理定律，理解气体等容变化的等温线的意义
2、理解热力学温标和绝对零度的意义，掌握热力学温度
和摄氏温度的换算关系
3、掌握理想气体的状态方程
教学过程：
一、查理定律
1、对一定质量的气体：Pt=P0+
t=P0(1+
)
Þ 当t=t1时, P1=P0(1+
)
当t=t2时, P2=P0(1+
)
Þ DP=Dt,
当Dt =10C时，DP=.
2、内容：一定质量的气体，在体积保持不变的情况下，温度每升高或降低10C，增加或降低的压强等于它在00C时压强的
。
Pt=P0+t=P0(1+)
3、等容线
一定质量的气体，在何种不变的情况下，P-t的关系图线是：
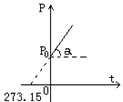一条一次函数图线
（1）截距 P0
（2）斜率 k==tga
（3）图线与x轴的交点Pt=0=P0+tÞ t=-2730C.
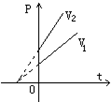结论：一定质量的气体，在不同体积下
的等容线是一簇一次函数图线，体积越大，
图线越靠近t轴，但所有图线与t 轴的交点都
是-2730C.
V1>V2
二、热力学温标
1、热力学温标：也叫绝对温标，由英国的威廉·汤姆逊创立。热力学温度的零度是-273.150C，简称为O开（K），叫做绝对零度。热力学温度与摄氏温度间的关系为：
T=t+273.15
注意：10C¹1K，但温度变化10C和变化1K是一样的。
2、查理定律
引入热力学温标后，查理定律将简化为：
=
。
即：一定质量的气体在体积不变的情况下，其压强与热力学温度成正比。
三、理想气体状态方程
1、理想气体
一、理想气体模型
是一种理想化的模型，一种科学的抽象
（1）分子本身的大小与它们之间的间距相比可以忽略不计：即分子有质量无大小，可视为质点，表示分子非常稀疏，相互作用力很小。
（2）分子间作用力为短程力，忽略不计分子间的相互作用力，分子间只有在相互碰撞或与器壁撞时才有力的作用。
（3）分子间或分子与器壁间的碰撞均为弹性碰撞
从宏观上说，理想气体严格遵循三个实验定律，而其内能就是内部分子动能的总和，不包含分子势能。因此其内能仅仅为T的函数，与气体体积无关。T，内能；T¯，内能¯。
在实际中常温常压下的所有真实气体均可近似看作理想气体。
2、理想气体状态方程
一定质量的理想气体，从初状态（P1，V1，T1）变化到末状态（P2，V2，T2），其压强和体积的乘积与热力学温度的比值是不变的。
=
=恒量
例题分析：
例1、如图所示，两端封闭、粗细均匀的竖直放
置的玻璃管内，有一长为h的水银柱，将管内气体分
为A、B两部分，A端空气柱的长度大于B端空气柱
的长度。现将其完全插入温度高于室温的热水中去，
管内水银柱将如何移动？
分析：水银柱原来处于平衡，则可知：PB=PA+h
温度升高，两部分气体压强都增大，若两部分气体压强变化不一致，则水银柱所受合外力不为零，水银柱将移动。若DPB>DPA，则向上移动；若DPA>DPB，则向下移动。所以判断水银柱是否移动，即是分析其所受合外力方向如何，就方向两部分气体的压强增大情况。
（1）假设法：假设水银柱不动，两部分气体做等容变化。
对A气体，由查理定律可得：
=
ÞPA'=
PAÞDPA=
PA.
对B气体，由查理定律可得：
=
ÞPB'=
PBÞDPB=
PB.
∵ TA=TB，DTA=DTB，PB=PA+h>PA
Þ DPB> DPA.
\ 水银柱上移。
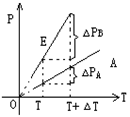（2）图象法 在同一P-T图上画出两部分气体
的等容线，如图所示。
在温度相同时，PB>PA, \ B气体图线斜率
较大，从图中可知：
DPB> DPA. \ 水银柱上移。
例2．一容器的容积为103cm3, 内装有一定质量的氧气，压强为3atm, 此时温度t=230C, 试求此容器中的氧分子个数N=？
分析：以气体为研究对象。由于任何1mol 的气体在标况下的体积都为22.4L，且含有阿佛加德罗常数个粒子，所以引入标况为气体的末态。
初态：P1=3atm V1=103cm3 T1=t+273=300K
末态：P2=1atm V2=? T2=0+273=273K
由理想气体的状态方程有：=
Þ V2=
=
=2.73´103(cm3)=2.73L
N=
NA=
´6.02´1023»7.3´1022(个)。
例3．圆柱形气缸质量10kg，倒置在水平粗糙
的地面上，气缸内部封有一定质量的空气，缸壁厚
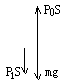度不计，缸内光滑活塞的质量为5kg,截面积为50cm2，当缸内气体温度为270C时，活塞与地面相接触但对地面恰无压力，当缸内气体温度为多少时，气缸壁对地面的压力为零（大气压强为P0=10´ 105pa）。
分析：当活塞对地面无压力时，活塞受力如图
ÞP0S=P1S+mg
Þ P1=P0-
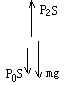=1.0´ 105-
=0.9´ 105(pa).
当气缸壁对地面压力为0时，缸壁受力如图：
ÞP2S=P0S+MgÞP2=P0+
=1.0´ 105+
=1.2´ 105(pa).
此时气体压强增大，活塞压紧地面，气体体积未发生变化，以气体为研究对象： P1=0.9´ 105(pa). V T1=t+273=300K
P2=1.2´ 105(pa) V T2=?
由查理定律有： =ÞT2=
T1=
´300=400(K).
课堂练习：
1．将一定质量的气体封闭于容器中，下列说法正确的是（ ）。
A、温度下降一半，则压强和体积分别降为原来的一半。
B、若压强降为原来的一半，则可能体积增加一倍，温度降低一半。
C、若体积增为原来的2倍，则可能压强减小一半，温度不变。
D、若压强增为原来的2倍，则可能体积缩小一半，温度升为原来的2倍。
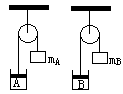2．如图所示，A、B两个一样的气缸中分别盛有等质量的同种气体，温度也相同。A、B气缸中的活塞分别通过滑轮系统挂一重物，质量分别为mA,mB，且mA>mB。若不计摩擦，当它们中的气体均升高100C温度后，则（ ）。
A、mB下降的高度比mA大。
B、mB下降的高度比mA 小。
C、mB与mA下降的高度一样大。
D、两重物下降高度无法确定谁大。
3．一个盛有空气的光滑气缸，底面积为100cm2，缸内有一能上下移动的活塞，活塞重力不计，当缸内气体压强和大气压强相等为105pa，且温度为270C时，活塞离缸底0.6m，在活塞上放一个1000N的重物，活塞下降，缸内体温度为320C，求活塞下降的距离Dh。
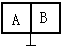4．如图，用销钉固定的活塞将水平放置的容器隔
成A和B两部分，其体积之比为VA：VB=2：1，
起初A中有温度为270C，压强为1.8´105pa的空
气，B中有温度为1270C，压强为1.2´105pa的空气。拔出销钉使活塞可以无摩擦地移动（无漏气）由于容器壁缓慢导热，最后气体都变成270C，活塞也停住，求最后A中气体的压强。